[INFO3] Probekurs – Einblick in unser Lernsystem [INFO3] PH3 – Weg-Zeit-Diagramm bei gleichmäßig beschleunigter Bewegung (inkl. Video)

Kapitel 5 von 44

wird bearbeitet

← Zurück Weiter→

[INFO3] PH3 – Weg-Zeit-Diagramm bei gleichmäßig beschleunigter Bewegung (inkl. Video)

dein_dozent_jan

Dieser Kurstext ist ein Auszug aus unserem Onlinekurs: PH3 – Einführung in die Kinematik

Nachdem du bereits das Beschleunigungs-Zeit-Diagramm und das Geschwindigkeits-Zeit-Diagramm für die gleichmäßig beschleunigte Bewegung kennengelernt hast, wollen wir uns in dieser Lerneinheit das Weg-Zeit-Diagramm (s-t-Diagramm) anschauen.

Bei der gleichmäßig beschleunigten Bewegung (=konstante Beschleunigung) ergibt sich im Weg-Zeit-Diagramm eine Parabel. Die Zeit $t$ in Sekunden [s] wird auf der x-Achse abgetragen, der Weg $s$ in Metern [m] auf der y-Achse.

Eine Parabel ist der Graph einer quadratischen Funktion. Ist die Parabel nach oben geöffnet, so ist der Scheitelpunkt der tiefste Punkt der Funktion. Ist die Parabel nach unten geöffnet, so ist der Scheitelpunkt der höchste Punkt der Funktion. In der obigen linken Grafik siehst du eine nach unten geöffnete Parabel, in der rechten Grafik eine nach oben geöffnete Parabel.

Innerhalb eines Weg-Zeit-Diagramms wird nur der zurückgelegte Weg betrachtet, d.h. die Funktion bewegt sich immer weiter in positive y-Richtung fort. Demnach werden die Teile der Parabel die eine negative Steigung aufweisen (also abnehmen) innerhalb des Weg-Zeit-Diagramms nicht berücksichtigt:

Du siehst in der obigen Grafik die Teile der Parabel, die eine positive Steigung aufweisen. In der linken Grafik ist der Teil einer nach unten geöffneten Parabel gegeben. Hier nimmt der Weg pro Zeit immer weiter ab, ein Körper legt also pro Zeiteinheit (z.B. pro Sekunde) immer weniger Weg (z.B. Meter) zurück. Dieser Fall tritt auf, wenn eine Verzögerung (negative Beschleunigung) vorliegt. Hier kann als Beispiel ein Bremsvorgang genannt werden, um die Geschwindigkeit zu verringern.

In der rechten Grafik ist der Teil einer nach oben geöffneten Parabel gegeben. Hier nimmt der Weg pro Zeit immer weiter zu, ein Körper legt also pro Zeiteinheit immer mehr Weg zurück. Dieser Fall ist gegeben, wenn eine positive Beschleunigung vorliegt. Ein Beispiel wäre die Beschleunigung eines Fahrzeugs zur Erhöhung der Geschwindigkeit.

Beispiel: Weg-Zeit-Diagramm bei gleichmäßig beschleunigter Bewegung

In dem folgenden Weg-Zeit-Diagramm ist die Weg-Zeit-Funktion für eine konstante Beschleunigung von 2 m/s² ohne Anfangsgeschwindigkeit eingezeichnet:

Weg-Zeit-Diagramm: positive Beschleunigung

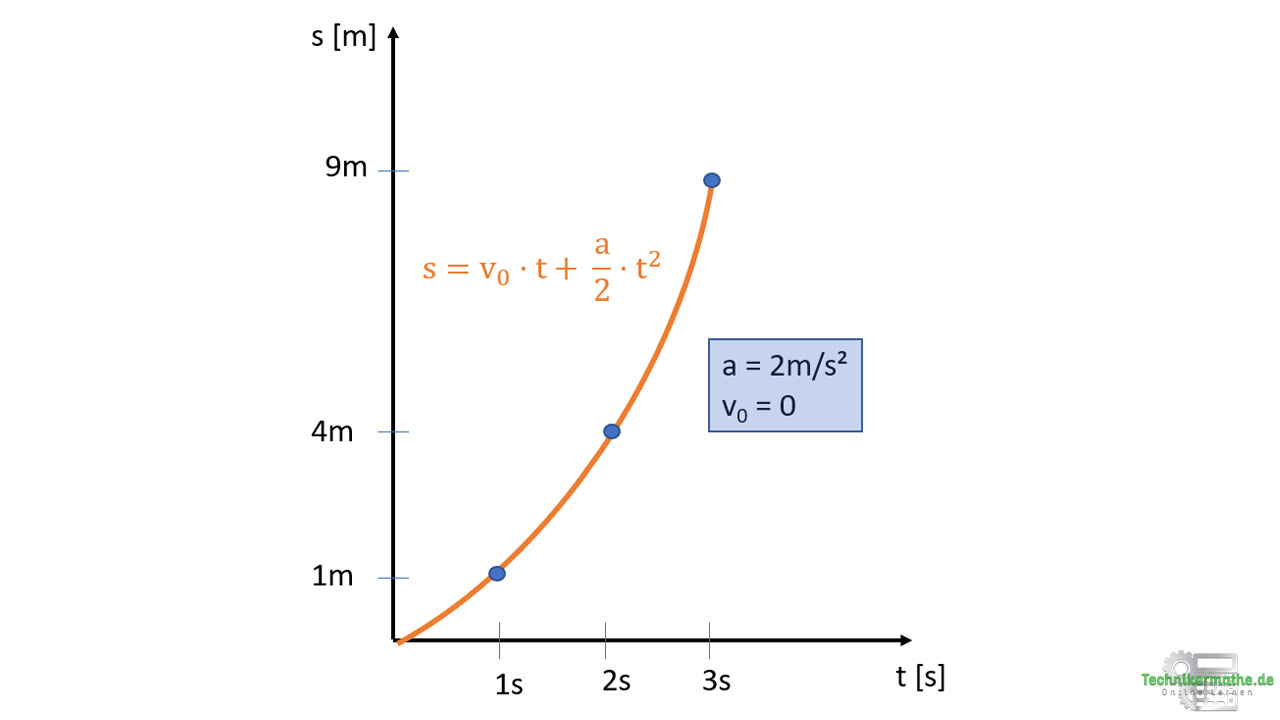
Beispiel

Die Weg-Zeit-Funktion ist eine nach oben geöffnete Parabel, da die Beschleunigung positiv ist. Wählen wir zum Beispiel als Zeitabstand immer 1 Sekunde, so nimmt die Wegdifferenz mit jeder Sekunde zu. Von Sekunde 0 bis 1 legt das Fahrzeug einen Weg von 1 Meter zurück, von 1s bis 2s einen Weg von 3 Metern zurück und von 2s bis 3s einen Weg von 5 m. Jede weitere Sekunde nimmt die Wegdifferenz zu.

Du kannst den Weg mittels der folgenden Gleichung berechnen:

$s = v_0 \cdot t + \dfrac{1}{2} \cdot a \cdot t^2$

Betrachten wir nun das Weg-Zeit-Diagramm, wenn eine negative Beschleunigung gegeben ist:

Weg-Zeit-Diagramm: Negative Beschleunigung

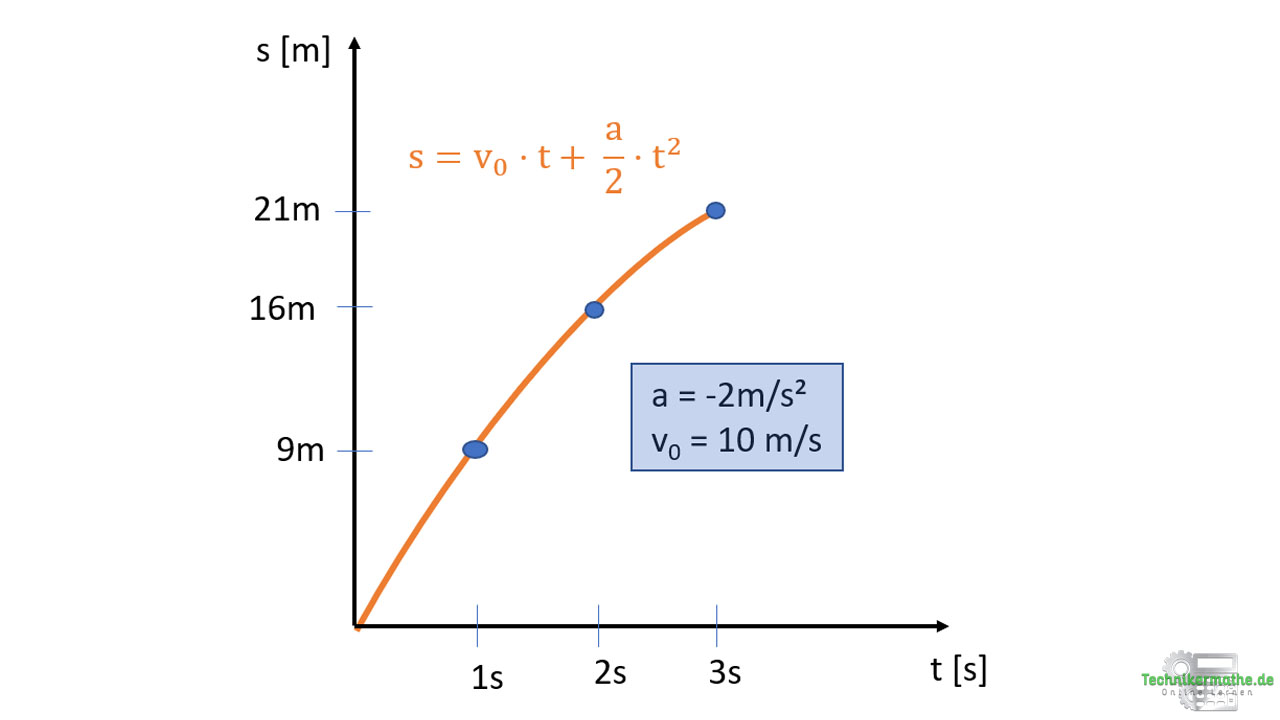
Die obige Grafik zeigt eine nach unten geöffnete parabelförmige Weg-Zeit-Funktion, die gegeben ist, wenn die konstante Beschleunigung negativ ist (=Verzögerung).

Wählen wir zum Beispiel als Zeitabstand immer 1 Sekunde, so nimmt die Wegdifferenz bei der linken Grafik mit jeder Sekunde ab. Von Sekunde 0 bis 1 legt das Fahrzeug einen Weg von 9 Meter zurück. Von Sekunde 1 bis 2 legt das Fahrzeug nur noch einen Weg von 7m Metern zurück und von Sekunde 2 bis 3 einen Weg von 5m. Jede weitere Sekunde nimmt die Wegdifferenz ab.

Merk’s dir!

Bei parabelförmigen Weg-Zeit-Funktionen ist die Wegdifferenz in gleichen Zeitabständen nicht mehr konstant. Somit nimmt bei einer positiven Beschleunigung die Wegdifferenz mit der Zeit zu, bei negativer Beschleunigung nimmt die Wegdifferenz mit der Zeit ab.

Ist eine negative Beschleunigung gegeben, dann muss das Fahrzeug natürlich eine Anfangsgeschwindigkeit aufweisen. Denn ohne Anfangsgeschwindigkeit keine Verzögerung (ohne Geschwindigkeit kein Bremsvorgang). Ist eine positive Beschleunigung gegeben, so muss das Fahrzeug keine Anfangsgeschwindigkeit aufweisen, da auch aus dem Stand beschleunigt werden kann.

Videoclip: Weg-Zeit-Funktionen

Im folgenden Video betrachten wir nochmal die unterschiedlichen Weg-Zeit-Funktionen bei einer positiven und einer negativer Beschleunigung.

Im nachfolgenden Beispiel wollen wir den Weg berechnen, welchen ein Fahrzeug zurücklegt. Du benötigst hierzu die Gleichungen der gleichförmigen und der gleichmäßig beschleunigten Bewegung.

Gleichförmige Bewegung

$s = v \cdot t$

$v = \dfrac{s}{t}$

$t = \dfrac{s}{v}$

Gleichmäßig beschleunigte Bewegung

$s = v_0 \cdot t + \dfrac{1}{2} \cdot a \cdot t^2$

$v = a \cdot t + v_0$

$t = \dfrac{v - v_0}{a}$

Beispiel: Berechnung des Weges

Gegeben ist ein Fahrzeug welches sich

-5 Sekunden mit konstanter Geschwindigkeit von 30 km/h bewegt.

-Danach wird das Fahrzeug 2 Sekunden lang mit 1,5 m/s² konstant beschleunigt.

-Das Fahrzeug wird dann innerhalb von 1s mit einer konstanten Beschleunigung von 1 m/s² abgebremst.

Wie groß ist der insgesamt zurückgelegte Weg?

Das Fahrzeug bewegt sich zunächst mit konstanter Geschwindigkeit von 30 km/h. Wir müssen hier zunächst die Geschwindigkeit in m/s umrechnen. Dazu verwenden wir den bekannten Faktor 3,6:

$v = 30 : 3,6 = 8,33 \frac{m}{s}$

Es handelt sich um eine gleichförmige Bewegung. Zur Berechnung des Weges verwenden wir damit die folgende Formel:

$s = v \cdot t$

Wir setzen nun die Geschwindigkeit v = 8,33 m/s sowie die Zeit von t = 5s in die Gleichung ein:

$s = v \cdot t = 8,33 \frac{m}{s} \cdot 5s = 41,65 m$

Das Fahrzeug legt in 5 Sekunden einen Weg von 41,65 Meter zurück.

Danach wird das Fahrzeug mit a = 1,5 m/s für t = 2 Sekunden beschleunigt. Es handelt sich hierbei um eine beschleunigte Bewegung. Den Weg berechnen wir über die folgende Gleichung:

$s = v_0 \cdot t + \dfrac{1}{2} \cdot a \cdot t^2$

Einsetzen der Werte:

$s = v_0 \cdot t + \dfrac{1}{2} \cdot a \cdot t^2 = 8,33 \frac{m}{s}\cdot 2s + \dfrac{1}{2} \cdot 1,5 \dfrac{m}{s^2} \cdot (2s)^2 = 19,66 m$

Der zurückgelegte Weg beträgt innerhalb dieses Beschleunigungsvorgangs 19,66 Meter.

Das Fahrzeug erreicht am Ende dieser Beschleunigung eine Geschwindigkeit $v$ von:

$v = a \cdot t + v_0 = 1,5 \dfrac{m}{s^2} \cdot 2s + 8,33 \dfrac{m}{s} = 11,33 \frac{m}{s}$ .

Als nächstes wird das Fahrzeug 1 Sekunde mit a = -1 m/s² abgebremst. Die Beschleunigung ist hier negativ, da es sich um eine Verzögerung handelt. Wir verwenden hier wieder die folgenden Formel für den Weg bei einer beschleunigten Bewegung:

$s = v_0 \cdot t + \dfrac{1}{2} \cdot a \cdot t^2$

Die Anfangsgeschwindigkeit dieses Bremsvorgangs entspricht der Endgeschwindigkeit der vorangegangenen Bewegung v₀ = 11,33 m/s.

$s = v_0 \cdot t + \dfrac{1}{2} \cdot a \cdot t^2 = 11,33 \dfrac{m}{s} \cdot 1s + \dfrac{1}{2} \cdot (-1 \dfrac{m}{s^2}) \cdot (1s)^2 = 10,83m$

Das Fahrzeug legt während des Bremsvorgangs einen Weg von 10,83 Meter zurück.

Der gesamte zurückgelegte Weg beträgt:

$s = 41,65 m + 19,66m + 10,83m = 72,14m$

In der nächsten Lerneinheit schauen wir uns mal den Sonderfall der gleichmäßig beschleunigten Bewegung an: Den freien Fall.

[INFO3] Probekurs - Einblick in unser Lernsystem

Physik 1 (PH1) - Grundlagen der Physik

[INFO3] PH3 – Weg-Zeit-Diagramm bei gleichmäßig beschleunigter Bewegung (inkl. Video)

dein_dozent_jan

Beispiel: Weg-Zeit-Diagramm bei gleichmäßig beschleunigter Bewegung

Beispiel

Videoclip: Weg-Zeit-Funktionen

Beispiel: Berechnung des Weges