[INFO3] Probekurs – Einblick in unser Lernsystem [INFO3] ET7 – Reihenschwingkreise

Kapitel 25 von 44

wird bearbeitet

← Zurück Weiter→

[INFO3] ET7 – Reihenschwingkreise

dein_dozent_jan

Dieser Kurstext ist ein Auszug aus unserem Onlinekurs: ET7 – Wechselstromtechnik 2

Nachdem wir im vergangenen Kurstext die Schwingkreise allgemein thematisiert haben, vertiefen wir nun dein Wissen und erklären dir was es mit den Reihenschwingkreisen auf sich hat. Dabei handelt es sich um eine RLC-Reihenschaltung.

Reihenschwingkreis – Grundlagen

Je nach Anordnung von Spule (Induktivität) oder Kondensator (Kapazität) in einem Netzwerk, sprechen wir entweder von einem Reihen– oder Parallel-Schwingkreise. Dabei unterscheiden wir ob die beiden Energiespeicher in Reihe oder parallel geschaltet sind.

Habt ihr irgendwelche Gemeinsamkeiten?….

Gemein haben beide Schaltungen, dass mit dem Ohmschen Widerstand drei Bauteile im Netzwerk vorhanden sind, von denen aber nur Spule und Kondensator als reaktive Komponenten angesehen werden. Man nennt so eine Schaltung – Schaltung zweiter Ordnung, denn sie werden durch Schwankungen der Netzfrequenz beeinflusst.

Kondensator und Spule haben einen gemeinsamen Frequenzpunkt, an welchem sie sich gegenseitig aufheben. Dies beeinflusst die Eigenschaften der Schaltung. Es handelt sich um den Resonanzfrequenzpunkt.

Die Reihenschaltung von Ohmschen Widerstand, Spule und Kondensator hat mit L und C zwei sich gegenseitig ergänzende Energiespeicher mit magnetischer (L) und elektrischer (C) Energie.

Erinnerst du dich?….

In Schwingkreisen laden sich Spulen und Kondensatoren gegenseitig immer wieder auf. Dabei entlädt sich der eine um den anderen aufzuladen und umgekehrt.

Dieser gegenseitige Ladungsvorgang und der damit verbundene Stromfluss setzt sich so lange fort, bis (zumindest bei der freien Schwingung, also ohne zusätzliche Energiezufuhr) die letzte Energie am Wirkwiderstand in Wärmeleistung an die Umgebung umgesetzt wurde.

Strom und Spannung sind bei den beiden Blindwiderständen ( $X_L$ und $X_C$ ) um 90° gegeneinander Phasen verschoben.

Wird der Reihenschwingkreis an einer Konstantspannungsquelle variabler Frequenz betrieben, kann der Amplituden- und Phasenfrequenzgang messtechnisch aufgenommen werden. Die Impedanz des Schwingkreises ist von der anliegenden Signalfrequenz abhängig und beeinflusst den Kreisstrom.

Reihenschwingkreise – Grafische Darstellung und Ermittlung

Jetzt folgt zuerst die Darstellung der RLC-Reihenschaltung in einem Schaltplan und anschließend die Vorgehensweise bei der Darstellung im Zeigerbild (Zeigerdiagramm).

Reihenschwingkreise – Darstellung im Schaltplan

In der nachfolgenden Abbildung findest du eine typische Darstellung einer in Reihe befindlichen Anordnung von Ohmschen Widerstand, Spule und Kondensator als Schaltplan.

Der Netzstrom $\underline{I}$ der alle Elemente durchfließt ist, wie für eine Reihenschaltung üblich, an allen Stellen im Netzwerk identisch (konstant). Anders verhält es sich mit den Spannungen. Diese variieren und sind deshalb einzeln aufgeführt mit $\underline{U}, \underline{U}_R, \underline{U}_L, \underline{U}_C$

Reihenschwingkreis - RLC-Reihenschaltung — Reihenschwingkreis – RLC-Reihenschaltung

Reihenschwingkreise – Darstellung im Zeigerbild

Wie gewohnt zeichnen wir zuerst den Stromzeiger auf der X-Achse liegen ein. Bei der Reihenschaltung hat dieser für alle Spannungen den gleichen Bezug.

Der Spannungszeiger des Ohmschen Widerstandes $\underline{U}_R$ liegt in der gleichen Phase wie der Stromzeiger und wird deshalb auf diesem abgelegt.

ET5 14 Reihenschwingkreise 02 — Zeigerbild – Spannungszeiger

Der Spannungszeiger der Spule (Induktivität) $\underline{U}_L$ wird vertikal, also im 90 ° Winkel zum Stromzeiger und Spannungszeiger eingezeichnet. Dabei legen wir dessen Ende an die Spitze des Spannungszeigers von $\underline{U}_R$ .

Zeigerbild - Spannungszeiger — Zeigerbild – Spannungszeiger

Der Spannungszeiger des Kondensators (Kapazität) $\underline{U}_C$ wird in die entgegengesetzte Richtung zum Spannungszeiger von $\underline{U}_L$ und vertikal, also im -90° Winkel zum Spannungszeiger von eingezeichnet $\underline{U}_R$ . Dessen Ende an der Spitze des Spannungszeigers von $\underline{U}_L$ liegt.

Der Spannungszeiger der Netzspannung $\underline{U}$ stellt die Strecke zwischen dem Ende des Spannungszeigers $\underline{U}_R$ (Koordinatenursprung) und der Spitze von $\underline{U}_C$ dar und kann jetzt final eingezeichnet werden.

ET5 14 Reihenschwingkreise 05 — Zeigerbild – Spannungszeiger

Den Phasenverschiebungswinkel $\varphi$ zeichnen wir dann im letzten Schritt ein.

Zeigerbild - Phasenverschiebungswinkel — Zeigerbild – Phasenverschiebungswinkel

Es zeigt sich ganz eindeutig, dass dieser einen positiven Wert annimmt.

Reihenschwingkreise – Berechnung

Wie du bereits weißt muss der Netzstrom nicht für die einzelnen Bauteile im Netzwerk errechnet werden, da er überall konstant ist. Die Spannung, der Phasenverschiebungswinkel und die Resonanz sind jedoch Größen, die ausgerechnet werden müssen.

Reihenschwingkreise – Berechnung der Netzspannung und Teilspannungen

Nachfolgend findest du die Gleichungen mit denen die Spannungen allgemein und unter Anwendung des Spannungsdreiecks [Satz des Pythagoras] berechnet werden können.

Netzspannung allgemein

Die Gleichung für die Netzspannung können wir wie gewohnt nach der Rechenregel für Reihenschaltungen ermitteln.

Getreu dem Motto “in Summe ist alles 0” und “was reingeht muss auch rauskommen” – Freie Formulierung des Knotensatzes.

$\boxed{ \underline{U} = \underline{U}_R + \underline{U}_L + \underline{U}_C }$

Jetzt fehlen uns aber noch die Werte für die einzelnen Spannungen (Teilspannungen) am Widerstand, an der Spule und am Kondensator.

Wir rechnen hier mit den Effektivwerten weiter!

Teilspannung am Ohmschen Widerstand

$\boxed{ U_R = I \cdot R}$

Teilspannung an der Spule (Induktivität)

$\boxed{ U_L = I \cdot \omega \cdot L }$

Teilspannung am Kondensator (Kapazität)

$\boxed{U_C = I \cdot \frac{1}{\omega \cdot C} }$

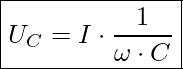
Netzspannung aus Spannungsdreieck

In der Vergangenheit konnten wir immer direkt mit der Anwendung des Satz des Pythagoras bei Spannungsdreiecken starten.

Dies geht hier aufgrund der Strecke von $\underline{U}_C$ hier nicht mehr ohne weiteres.

Um dem Problem Herr zu werden, subtrahieren wir $\underline{U}_C$ mit $U_C$ (Effektivwert) aus der Gleichung. Das hat den Vorteil, dass auch die zu lang geratene Strecke $\underline{U}_L$ korrekt verkürzt wird und wir den Satz des Pythagoras anwenden können.

Reihenschwingkreis - Satz des Pythagoras — Reihenschwingkreise – Satz des Pythagoras

Es gilt also:

$\boxed{U = \sqrt{ U_R^2 + (U_L - U_C)^2} }$

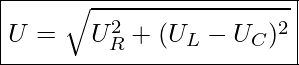
Wenn wir uns jedoch die Netzspannung mit den Werten aus den Spannungsgleichungen ermitteln möchten, dann sieht das wie folgt aus:

$\boxed{U = I \cdot \sqrt{R^2 + (\omega \cdot L - \frac{1}{\omega \cdot C})^2} }$

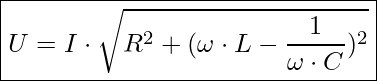
Reihenschwingkreise – Berechnung des Phasenverschiebungswinkels

Den Phasenverschiebungswinkel können wir ganz einfach aus dem Zeigerdiagramm (Rechtwinkligen Spannungsdreieck) ermitteln.

$\boxed{tan \varphi = \frac{U_L - U_C}{U_R} }$

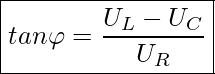
oder mit den Werten aus den Spannungsleichungen

$\boxed{ tan \varphi = \frac{\omega \cdot L - \frac{1}{\omega \cdot C}}{R} }$

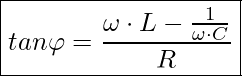
Reihenschwingkreise – Berechnung der Resonanz

Aus unseren bisherigen Gleichungen für die Spannungen und den Phasenverschiebungswinkel können wir ableiten, dass der Netzstrom $I$ bei der gegebenen Netzspannung $U$ und einem vorliegenden Widerstand $R$ infolge der Reihenresonanz maximal wird.

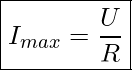$\boxed{ I_{max} = \frac{U}{R} }$ – Thomsonsche Formel für Reihenschwingkreise | Maximalwert

Dies setzt jedoch voraus, dass $U_L$ und $U_C$ identisch sind und sich damit in der Berechnung gegenseitig aufheben:

$\boxed{ \omega \cdot L - \frac{1}{\omega \cdot C} = 0}$

Merk’s dir!

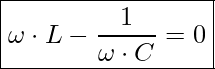
Bei einem mit $L$ und $C$ gleich dimensionierten Reihen- und Parallelschwingkreis hat dieselbe Resonanzfrequenz. Das bedeutet, dass die Thomsonsche Schwingungsformel zur Berechnung unverändert für beide bleibt.

Darstellung der Reihenresonanz (Resonanz) im Zeigerbild

Zum Abschluss dieser Lerneinheit stellen wir noch eben schnell das Zeigerbild für die Reihenresonanz, besser gesagt von dessen Wirkung.

Wie in der Letzten Gleichung schon ersichtlich, heben sich die beiden Teilspannung $\underline{U}_L$ und $\underline{U}_C$ gegenseitig auf. Dies untermalt die oben getätigte Aussage zum Resonanzfrequenzpunkt.

Daraus leiten wir folgenden Zusammenhänge im Zeigerdiagramm ab:

$\boxed{ \underline{U}_L = - \underline{U}_C }$

das bedeutet

$\boxed{\underline{U} = \underline{U}_R }$

Bei den Effektivwerten haben wir folgenden Zusammenhang:

$\boxed{ U_L = U_C }$