[INFO3] Probekurs – Einblick in unser Lernsystem [INFO3] PH3 – Schräger Wurf (inkl. Video)

Kapitel 6 von 44

wird bearbeitet

← Zurück Weiter→

[INFO3] PH3 – Schräger Wurf (inkl. Video)

deine_dozentin_jessica

Dieser Kurstext ist ein Auszug aus unserem Onlinekurs: PH3 – Einführung in die Kinematik

In dieser Lektion schauen wir uns den schrägen Wurf an, die Gleichungen, die du dafür benötigst sowie ein ausführliches Berechnungsbeispiel.

Beim schrägen Wurf erfolgt eine gleichförmige Bewegung (=konstante Geschwindigkeit) in x-Richtung und eine gleichmäßig beschleunigte Bewegung (=konstante Beschleunigung) in y-Richtung. Die beiden Bewegungen die auftreten sind identisch zum waagerechten Wurf. Der Unterscheid zum waagerechten Wurf ist, dass der Körper nicht waagerecht, sondern schräg abgeworfen wird. Die Anfangsgeschwindigkeit $v_0$ ist demnach nicht, wie beim waagerechten Wurf, gleich der Geschwindigkeit $v_x$ in x-Richtung.

Schräger Wurf: Geschwindigkeiten

Die Anfangsgeschwindigkeit $v_0$ muss beim schrägen Wurf in eine Geschwindigkeit $v_{0x}$ in x-Richtung und eine Geschwindigkeit $v_{0y}$ in y-Richtung zerlegt werden. Die Zerlegung der Geschwindigkeit erfolgt über das bereits bekannte Vorgehen der Zerlegung von Kräften.

Merk’s dir!

$v_{0x} = v_0 \cdot \cos(\alpha)$ Zerlegung in x-Richtung (horizontal)

$v_{0y} = v_0 \cdot \sin(\alpha)$ Zerlegung in y-Richtung (vertikal)

Die Bewegung in x-Richtung erfolgt durch den waagerechten Anteil des Abwurfs. Die Bewegung in y-Richtung erfolgt einmal durch den Anteil des Abwurfs in die Höhe sowie durch die Erdanziehung des Körpers nach unten mit der Fallbeschleunigung $g = 9,81 \frac{m}{s^2}$ . Die Wurfbahn beim schrägen Wurf ist, wie beim waagerechten Wurf, eine Parabel.

Betrachten wir den schrägen Wurf mal etwas genauer:

Die erste Bewegung ist die Abwurfbewegung in x- und y-Richtung, es erfolgt also ein schräger Wurf. Hier muss die Anfangsgeschwindigkeit 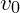$v_0$ (auch: Abwurfgeschwindigkeit) in eine x- und eine y-Komponente zerlegt werden.
Die Bewegung in x-Richtung erfolgt über den gesamten Wurf mit konstanter Geschwindigkeit (=gleichförmige Bewegung). Die Bewegung in y-Richtung entspricht dem senkrechten Wurf nach oben und setzt sich aus der Abwurfgeschwindigkeit in y-Richtung sowie der Fallbeschleunigung 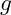$g$ zusammen.
Die Abwurfgeschwindigkeit 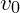$v_0$ und die Aufprallgeschwindigkeit sind identisch, wenn die Höhe des Abwurfs mit der Höhe des Aufpralls übereinstimmt.
Die gesamte Flugdauer entspricht der zweifachen Steigzeit ( 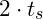$2 \cdot t_s$ ), da Steigzeit und Fallzeit identisch sind, wenn Abwurf- und Aufprallgeschwindigkeit übereinstimmen.

Schräger Wurf: Gleichungen

Für die Bewegung in x-Richtung verwenden wir die Gleichungen der gleichförmigen Bewegung und für die Bewegung in y-Richtung die Gleichungen für den senkrechten Wurf nach oben. Wir ersetzen dabei die Geschwindigkeiten durch die oben berechneten Geschwindigkeitskomponenten und erhalten dann die Gleichungen für den schrägen Wurf:

Bewegung in x-Richtung (gleichförmige Bewegung):
$s_x = v_0 \cdot \cos(\alpha) \cdot t$	Wurfweite in Abhängigkeit von der Zeit
$s_x = v_0 \cdot \cos(\alpha) \cdot T$	Gesamte Wurfweite
Bewegung in y-Richtung (senkrechter Wurf nach oben)
$s_y = v_0 \cdot \sin(\alpha) \cdot t - \dfrac{1}{2} \cdot g \cdot t^2$	Wurfhöhe in Abhängigkeit von der Zeit
$h_{max} = v_0 \cdot \sin(\alpha) \cdot t_s - \dfrac{1}{2} \cdot g \cdot t_s^2$	max. Höhe /Scheitelhöhe in Abhängigkeit von der Zeit
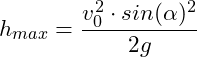$h_{max} = \dfrac{v_0^2 \cdot sin(\alpha)^2 }{2g}$	max. Höhe/ Scheitelhöhe
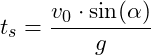$t_s = \dfrac{v_0 \cdot \sin(\alpha)}{g}$	Steigzeit
$T = 2 \cdot t_s$	Wurfzeit
Geschwindigkeiten
$v_{0x} = v_0 \cdot \cos(\alpha)$	Geschwindigkeit in x-Richtung
$v_{0y} = v_0 \cdot \sin(\alpha) - g \cdot t$	Geschwindigkeit in y-Richtung
$v = \sqrt{v_{0x}^2 + v_{0y}^2}$	Resultierende Geschwindigkeit

Videos: Schräger Wurf

In den nachfolgenden Videos zeige ich dir nochmals auf, welche Gleichungen du benötigst und wie du die Berechnungen durchführst.

Beispiel: Schräger Wurf

Ein Ball wird mit 15 m/s unter einem Winkel von 29 Grad abgeworfen.

a) Wie hoch ist der Ball an seinem höchsten Punkt?

b) Nach welcher Zeit erreicht er den höchsten Punkt?

c) Wie weit fliegt der Ball insgesamt?

d) Wie lange fliegt der Ball insgesamt?

e) Mit welcher Geschwindigkeit trifft der Ball auf dem Boden auf?

Lösung zu a) Gesamthöhe

Wir haben die Anfangsgeschwindigkeit v₀ = 15 m/s gegeben, den Winkel α = 29° und die Fallbeschleunigung mit g = 9,81 m/s².

Wie hoch fliegt der Ball insgesamt?

Der höchste Punkt ist bei einer Parabel der Scheitelpunkt. Wir benötigen also für die Berechnung die folgende Gleichung:

$h_{max} = \dfrac{v_0^2 (\sin(\alpha))^2}{2 \cdot g}$

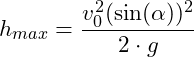
Einsetzen der Werte:

$h_{max} = \dfrac{(15 \frac{m}{s})^2 \cdot (\sin(29^\circ))^2}{2 \cdot 9,81 \frac{m}{s^2}} = 2,7 m$

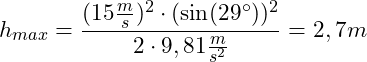
Der Ball erreicht eine Höhe von 2,7m.

Lösung zu b) Steigzeit

Nach welcher Zeit erreicht er den höchsten Punkt?

Der höchste Punkt ist die Scheitelhöhe der Parabel. Bevor der Ball die Scheitelhöhe erreicht, steigt er nach oben (Aufwärtsbewegung). Wir wollen also die Steigzeit $t_s$ bestimmen:

$t_s = \dfrac{v_0 \cdot \sin(\alpha)}{g}$

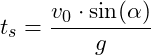
Einsetzen der Werte:

$t_s = \dfrac{15 \frac{m}{s} \cdot \sin(29^\circ)}{9,81 \frac{m}{s^2}} = 0,74s$

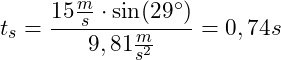
Der Ball benötigt bis zur Erreichung der Scheitelhöhe 0,74 Sekunden.

Lösung zu c) Wurfweite / Flugweite

Wie weit fliegt der Ball?

Wir wollen wissen, welchen Weg der Ball in x-Richtung zurücklegt (=Wurfweite). Dazu verwenden wir die folgende Gleichung:

$s_x = v_0 \cos(\alpha) \cdot 2 \cdot t_s$

Einsetzen der Werte:

$s_x = 15 \frac{m}{s} \cdot \cos(29^\circ) \cdot 2 \cdot t_s$

Wir benötigen zur Berechnung der Wurfweite noch die Steigzeit $t_s$ , die wir in Aufgabenteil b) berechnet haben:

$t_s = 0,74s$

Einsetzen:

$s_x = 15 \frac{m}{s} \cdot \cos(29^\circ) \cdot 2 \cdot 0,74s = 19,42m$

Der Ball legt einen Weg von 19,42 m zurück.

Lösung zu d) Steighöhe + Fallzeit

Wie lange fliegt der Ball insgesamt?

Steighöhe $t_s$ und Fallzeit $t_F$ sind in diesem Fall gleich, da der Ball vom Boden aus abgeworfen wird und demnach genauso hoch fliegt (bis zum Scheitelpunkt), wie er fällt (nach dem Scheitelpunkt). Demnach kannst du ganz einfach die Steigzeit $t_s$ mal zwei nehmen:

$T = 2 \cdot t_s = 2 \cdot 0,74s = 1,48s$

Der Ball fliegt insgesamt 1,48s.

Lösung zu e) Aufprallgeschwindigkeit

Wir wollen noch wissen, mit welcher Geschwindigkeit der Ball auf dem Boden aufkommt. Dazu müssen wir zunächst die beiden Geschwindigkeit beim Aufprall nach der Zeit $T = 1,48s$ berechnen.

$v_x = v_0 \cdot \cos(\alpha)$ Geschwindigkeit in x-Richtung

$v _y = v_{0} \cdot sin(\alpha) - g \cdot t_s$ Geschwindigkeit in y-Richtung

$v = \sqrt{v_x^2 + v_y^2}$ Aufprallgeschwindigkeit

Wir starten mit der Geschwindigkeit in $x$ -Richtung:

$v_x = v_0 \cdot \cos(\alpha)$

Diese ist konstant und damit zeitunabhängig:

$v_x = 15 \frac{m}{s} \cdot \cos(29^\circ) = 13,12 \frac{m}{s}$

Danach berechnen wir die Geschwindigkeit in y-Richtung:

$v _y = v_{0} \cdot sin(\alpha) - g \cdot t$

Diese ist gleichmäßig beschleunigt, also zeitabhängig mit $t = T = 1,48s$ :

$v _y = 15 \frac{m}{s} \cdot sin(29^\circ) - 9,81 \frac{m}{s^2} \cdot 1,48s = -7,25 \frac{m}{s}$

Das Minuszeichen resultiert, weil der Ball zunächst mit 15 m/s nach oben geworfen wird, dann aber nach unten fällt. Das Minuszeichen gibt also die entgegengesetzte Richtung zum Wurf (nach oben) an, die infolge der Erdanziehung resultiert.

Einsetzen in die folgende Gleichung:

$v = \sqrt{v_x^2 + v_y^2} = \sqrt{(13,12 \frac{m}{s})^2 + (-7,25 \frac{m}{s})^2}$

Nicht vergessen, dass das Minuszeichen mit quadriert wird und der Wert damit positiv wird:

$v = 14,98 \frac{m}{s} \approx 15 \frac{m}{s}$

Die Aufprallgeschwindigkeit beträgt 15 m/s.

Da die Abwurfhöhe und die Aufprallhöhe identisch sind, sind die Abwurfgeschwindigkeit und die Aufprallgeschwindigkeit ebenfalls identisch.

In der folgenden Lektion betrachten wir die gleichförmige Kreisbewegung.

[INFO3] Probekurs - Einblick in unser Lernsystem

Physik 1 (PH1) - Grundlagen der Physik

[INFO3] PH3 – Schräger Wurf (inkl. Video)

deine_dozentin_jessica

Schräger Wurf: Geschwindigkeiten

Schräger Wurf: Gleichungen

Videos: Schräger Wurf

Beispiel: Schräger Wurf

Lösung zu a) Gesamthöhe

Lösung zu b) Steigzeit

Lösung zu c) Wurfweite / Flugweite

Lösung zu d) Steighöhe + Fallzeit

Lösung zu e) Aufprallgeschwindigkeit