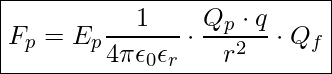[INFO3] Probekurs – Einblick in unser Lernsystem [INFO3] ET4 – Elektrisches Feld – Feldkraft

Kapitel 19 von 44

wird bearbeitet

← Zurück Weiter→

[INFO3] ET4 – Elektrisches Feld – Feldkraft

dein_dozent_jan

Dieser Kurstext ist ein Auszug aus unserem Onlinekurs: ET4 – Elektrische Felder

In diesem Kurstext erklären wir die was es mit der Feldkraft im elektrischen Feld auf Ladungsträger auf sich hat. Da bedeutet wir schauen uns die Feldkraft F genau an.

“Die Feldkraft F wirkt immer in die Richtung, in der das größte Potentialgefälle vorliegt. Ein Zickzack-Kurs oder Richtungswechsel treten im Normalfall nicht auf.”

Feldkraft im elektrischen Feld – Berechnung mit Feldstärke + Ladung

Liegt in einem elektrischen Feld eine elektrische Ladung Q vor, so wirkt auf diese eine Kraft $\vec{F}$ . Diese Kraft kann einfach ermittelt werden, wenn wir hierzu unsere bekannte Gleichung zur elektrischen Feldstärke einfach nach $\vec{F}$ auflösen:

$\boxed{ \vec{E} = \frac{\vec{F}}{Q} }$

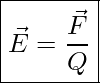
Kennzahlen:

$\boxed{\vec{E} = }$ Elektrische Feldstärke

$\boxed{\vec{F} = }$ Feldkraft

sowie

$\boxed{Q = }$ Elektrische Ladung

Dann erhalten wir:

$\boxed{\vec{F} = \vec{E} \cdot Q }$

Die Kraft ist also das Produkt aus elektrischer Ladung $Q$ und Feldstärke $\vec{E} }$ .

Falls du dich jetzt fragst, weshalb die Angabe mit Vektoren erfolgt, dann liegt das daran das beide Größen, also elektrische Feldstärke und Feldkraft richtungsabhängige Größen sind.

Feldkraft im elektrischen Feld – Gesetz nach Coulomb

Mit Hilfe des Coulombschen Gesetzes kannst du die Kraft zwischen zwei Punktladungen berechnen. Wie gewohnt gehen wir wieder von einer Probeladung $Q_p$ aus. Diese wird in das elektrische Feld gebracht, welches durch eine andere elektrische Ladung $Q_f$ erzeugt wurde. Infolgedessen wirkt jetzt auf beide Ladungen $Q_p$ und $Q_f$ eine Kraft $F$ .

Geladene Kugel - Feldkraft — Geladene Kugel – Feldkraft

Zum besseren Verständnis..

Damit du dir diesen Vorgang besser vorstellen kannst, befindet sich die elektrische Ladung $Q_f$ in einer geladenen Metallkugel und diese erzeugt ein radiales elektrisches Feld in das wir nun unsere Probeladung bewegen.

Da beide Ladungen in Wechselwirkung miteinander stehen, gilt hier das Wechselwirkungsprinzip, welches besagt, dass die Kraft auf beide Ladungen identisch sein muss.

Formal äußert sich dies durch:

$\boxed{F_p = F_f = E_p \cdot Q_p = E_f \cdot Q_f }$

Herleitung – der Feldkraft für das Radialfeld

Hier soll unsere Betrachtung aber noch nicht enden. Denn die Gleichung lässt sich noch weiter anpassen. Denn uns liegt ja ein Radialfeld vor.

Fläche der geladenen Kugel

Da es sich in unserer Überlegung um eine Kugel handelt, verwenden wir für die Oberfläche der Kugel folgende Formel

$\boxed{ A = 4 \pi r^2 }$

Flächenladungsdichte

Als weitere Größe führen wir nun die Flächenladungsdichte ein:

$\boxed{\sigma = \frac{Q}{A} }$

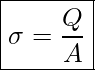
mit der Angabe der Kugeloberfläche erhalten wir die angepasste Gleichung:

$\boxed{\sigma = \frac{Q}{4 \pi r^2} }$

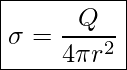
Somit können wir auch die Gleichung von oben entsprechend anpassen:

$\boxed{C = \frac{Q}{U} }$

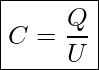
wird zu

$\boxed{C = \epsilon_0 \cdot \epsilon_r \frac{A}{D} }$

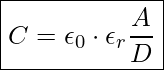
sowie

$\boxed{\frac{Q}{U} = \epsilon_0 \cdot \epsilon_r \cdot \frac{A}{d} }$

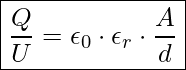
Dividieren durch $A$ und multiplizieren mit $U$ verändert die Gleichung zu:

$\boxed{\frac{Q}{A} = \epsilon_0 \cdot \epsilon_r \frac{U}{d} }$

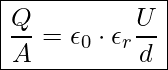
Elektrische Feldstärke für Radialfeld

Jetzt haben wir auf der linken Seite der Gleichung die Flächenladungsdichte $\sigma$ und auf der rechten Seite mit $\frac{U}{d}$ die Angabe der elektrischen Feldstärke formuliert.

Führen wir jetzt die Gleichungen

$\boxed{\sigma = \frac{Q}{4 \pi r^2} }$

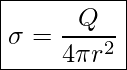
sowie

$\boxed{\sigma = \epsilon_0 \cdot \epsilon_r \cdot E }$

zusammen, so erhalten wir:

$\boxed{\frac{Q}{4 \pi r^2} = \epsilon_0 \cdot \epsilon_r \cdot E }$

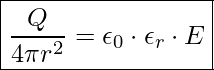
umgestellt nach E ergibt sich die Angabe der elektrischen Feldstärke

$\boxed{E = \frac{1}{4 \pi \epsilon_0 \cdot \epsilon_r} \cdot \frac{Q}{r^2} }$

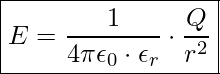
$\boxed{ r }$ ist übrigens der Abstand zum Kugelmittelpunkt.

Feldkraft im Radialfeld – Finale Gleichung

Jetzt haben wir alle Angaben die wir benötigen um die Kraft auf einen Körper im Radialfeld zu ermitteln.

Da noch immer das Wechselwirkungsprinzip sowohl für die Ladung der Kugel als auch für die Probeladung gilt, nehmen wir zur Bestimmung die Gleichung für die Probeladung und übertragen sie gedanklich auf die Kugel.

$\boxed{F = E \cdot q }$

Einsetzen der Gleichung für E ergibt dann:

$\boxed{F = \frac{1}{4 \pi \epsilon_0 \epsilon_r} \cdot \frac{Q \cdot q}{r^2} }$

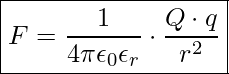
Jetzt haben wir das Coulomb’sche Gesetzt formuliert.

Nehmen wir nun die Gleichung von oben, in welcher wir die Zusammenhang zwischen den Ladungen formuliert haben, also

$\boxed{F_p = F_f = E_p \cdot Q_p = E_f \cdot Q_f }$

so können wir die Gleichung jetzt anpassen, zu:

$\boxed{F_p = E_p \frac{1}{4 \pi \epsilon_0 \epsilon_r} \cdot \frac{Q_p \cdot q}{r^2} \cdot Q_f }$

Nachdem wir die Feldkraft ermittelt haben, wollen wir im nächsten Kurstext die Bewegungsgeschwindigkeit im elektrischen Feld betrachten.

[INFO3] Probekurs - Einblick in unser Lernsystem

Physik 1 (PH1) - Grundlagen der Physik

[INFO3] ET4 – Elektrisches Feld – Feldkraft

dein_dozent_jan

Feldkraft im elektrischen Feld – Berechnung mit Feldstärke + Ladung

Feldkraft im elektrischen Feld – Gesetz nach Coulomb

Herleitung – der Feldkraft für das Radialfeld

Fläche der geladenen Kugel

Flächenladungsdichte

Elektrische Feldstärke für Radialfeld

Feldkraft im Radialfeld – Finale Gleichung