[INFO3] Probekurs – Einblick in unser Lernsystem [INFO3] ET7 – Parallelschwingkreise

Kapitel 26 von 44

wird bearbeitet

← Zurück Weiter→

[INFO3] ET7 – Parallelschwingkreise

dein_dozent_jan

Dieser Kurstext ist ein Auszug aus unserem Onlinekurs: ET7 – Wechselstromtechnik 2

Nachdem wir im vergangenen Kurstext die Reihenschwingkreise thematisiert haben, vertiefen wir nun dein Wissen zu den Schwingkreisen weiter und erklären dir was es mit den Parallelschwingkreisen auf sich hat. Dabei handelt es sich um eine RLC-Parallelschaltung.

Parallelschwingkreise – Grundlagen

Je nach Anordnung von Spule (Induktivität) oder Kondensator (Kapazität) in einem Netzwerk, sprechen wir entweder von einem Reihen- oder Parallel-Schwingkreise. Dabei unterscheiden wir ob die beiden Energiespeicher in Reihe oder parallel geschaltet sind.

Habt ihr irgendwelche Gemeinsamkeiten?…

Gemein haben beide Schaltungen, dass mit dem Ohmschen Widerstand drei Bauteile im Netzwerk vorhanden sind, von denen aber nur Spule und Kondensator als reaktive Komponenten angesehen werden. Man nennt so eine Schaltung – Schaltung zweiter Ordnung, denn sie werden durch Schwankungen der Netzfrequenz beeinflusst.

Kondensator und Spule haben einen gemeinsamen Frequenzpunkt, an welchem sie sich gegenseitig aufheben. Dies beeinflusst die Eigenschaften der Schaltung. Es handelt sich um den Resonanzfrequenzpunkt.

Der Kondensator kann in vielen Fällen als ideales Bauteil angesehen werden. Der Widerstand des Drahtes der Spule muss jedoch häufiger in Rechnungen berücksichtigt werden. Man zählt den Widerstand des Drahtes der Spule zum Wirkwiderstand.

Im Parallelschwingkreis bilden Kondensator und Spule eine Parallelschaltung. Der Spulenwiderstand muss in einen dazu äquivalenten Parallelwiderstand umgerechnet werden.

Beide sind 3-Element-Netzwerke, die zwei reaktive Komponenten enthalten, was sie zu einer Schaltung zweiter Ordnung macht, beide werden durch Schwankungen in der Netzfrequenz beeinflusst und beide haben einen Frequenzpunkt, an dem sich ihre beiden reaktiven Komponenten gegenseitig aufheben und die Eigenschaften der Schaltung beeinflussen. Beide Kreise haben einen Resonanzfrequenzpunkt.

Erinnerst du dich?…

Durch einen kurzen Energieimpuls wird der Schwingkreis “aktiviert” und infolge der charakteristischen Eigenfrequenz in der Amplitude beginnen die abnehmenden, gedämpften Schwingungen.

Dabei laden sich in den Schwingkreisen die Spule und der Kondensator gegenseitig immer wieder auf. So entlädt sich der eine um den anderen aufzuladen und umgekehrt.

Freie Schwingungen

Dieser gegenseitige Ladevorgang und der damit verbundene Stromfluss setzt sich so lange fort, bis (zumindest bei der freien Schwingungen, also bei einmaligem Energieimpuls ohne zusätzliche Energiezufuhr) die letzte Energie am Wirkwiderstand in Wärmeleistung an die Umgebung umgesetzt wurde.

Erzwungene Schwingungen

Findet eine dauerhafte Versorgung des Schwingkreises mit Energie durch eine Energiequelle statt (Erzwungene Schwingungen), so ergibt sich eine ausgeprägte Amplitude aufgrund der Resonanzfrequenz, sofern die Eigenfrequenz innerhalb des Frequenzbandes der Energiequelle vorhanden ist.

Strom und Spannung sind bei den beiden Blindwiderständen ( $X_L$ und $X_C$ ) um 90° gegeneinander Phasen verschoben. Daraus ergibt sich das gleiche Verhalten der einzelnen Ströme durch die Bauteile, zumal die Netzspannung ja an allen Widerständen konstant ist. Diesen Zusammenhang findest du gleich bei der Anfertigung des Zeigerbildes wieder.

Wird der Reihenschwingkreis an einer Konstantspannungsquelle variabler Frequenz betrieben, kann der Amplituden- und Phasenfrequenzgang messtechnisch aufgenommen werden. Die Impedanz des Schwingkreises ist von der anliegenden Signalfrequenz abhängig und beeinflusst den Kreisstrom.

Parallelschwingkreise – Grafische Darstellung und Ermittlung

Jetzt folgt zuerst die Darstellung der RLC-Parallelschaltung in einem Schaltplan und anschließend die Vorgehensweise bei der Darstellung im Zeigerbild (Zeigerdiagramm).

Parallelschwingkreise – Darstellung im Schaltplan

In der nachfolgenden Abbildung findest du eine typische Darstellung einer in Parallelschaltung befindlichen Anordnung von Ohmschen Widerstand, Spule und Kondensator als Schaltplan. Die Netzspannung $\underline{U}$ welche an allen Elementen anliegt, ist wie für eine Parallelschaltung üblich, an allen Stellen im Netzwerk identisch (konstant). Anders verhält es sich mit den Strömen. Diese variieren und sind deshalb einzeln aufgeführt mit $\underline{I}, \underline{I}_R, \underline{I}_L, \underline{I}_C$

Parallelschwingkreis - RLC-Parallelschaltung — Parallelschwingkreis – RLC-Parallelschaltung

Parallelschwingkreise – Darstellung im Zeigerbild

Wie gewohnt zeichnen wir zuerst den Spannungszeiger auf der X-Achse liegen ein. Bei der Parallelschaltung hat dieser für alle Ströme den gleichen Bezug.

Parallelschwingkreis - Spannungszeiger — Parallelschwingkreis – Spannungszeiger

Der Stromzeiger des Ohmschen Widerstandes $\underline{I}_R$ liegt in der gleichen Phase wie der Spannungszeiger und wird deshalb auf diesem abgelegt.

Parallelschwingkreis - Stromzeiger - Widerstand — Parallelschwingkreis – Spannungszeiger – Widerstand

Der Stromzeiger der Spule (Induktivität) $\underline{I}_L$ wird vertikal, also im -90 ° Winkel zum Stromzeiger und Spannungszeiger nach unten eingezeichnet. Dabei legen wir dessen Ende an die Spitze des Stromzeigers von $\underline{I}_R$ .

Parallelschwingkreis - Stromzeiger - Spule — Parallelschwingkreis – Stromzeiger – Spule

Der Stromzeiger des Kondensators (Kapazität) $\underline{I}_C$ wird in die entgegengesetzte Richtung zum Spannungszeiger von $\underline{I}_L$ und vertikal, also im 90° Winkel zum Stromzeiger von $\underline{I}_R$ eingezeichnet. Dessen Ende liegt an der Spitze des Stromzeigers von $\underline{I}_L$ .

Parallelschwingkreis - Stromzeiger - Kondensator — Parallelschwingkreis – Stromzeiger – Kondensator

Der Stromzeiger des Netzstroms $\underline{I}$ stellt die Strecke zwischen dem Ende des Stromzeigers $\underline{I}_R$ (Koordinatenursprung) und der Spitze von $\underline{I}_C$ dar und kann jetzt final eingezeichnet werden.

Parallelschwingkreis - Netzstrom — Parallelschwingkreis – Netzstrom

Den Phasenverschiebungswinkel $\varphi$ zeichnen wir dann im letzten Schritt ein.

Parallelschwingkreis - Phasenverschiebungswinkel — Parallelschwingkreis – Phasenverschiebungswinkel

Es zeigt sich ganz eindeutig, dass dieser einen positiven Wert annimmt.

Parallelschwingkreise – Berechnung

Wie du bereits weißt, muss die Netzspannung nicht für die einzelnen Zweige der Bauteile im Netzwerk errechnet werden, da sie überall konstant ist. Der Netzstrom, der Phasenverschiebungswinkel und die Resonanz sind jedoch Größen, die ausgerechnet werden müssen.

Parallelschwingkreise – Berechnung des Netzstroms und Teilströme

Nachfolgend findest du die Gleichungen mit denen den Netzstrom allgemein und unter Anwendung des Spannungsdreiecks [Satz des Pythagoras] berechnet werden können.

Netzstrom allgemein

Die Gleichung für die Netzstrom können wir wie gewohnt nach der Rechenregel für Reihenschaltungen ermitteln.

Getreu dem Motto “in Summe ist alles 0” und “was reingeht muss auch rauskommen” – Freie Formulierung des Knotensatzes.

$\boxed{ \underline{I} = \underline{I}_R + \underline{I}_L + \underline{I}_C }$

Jetzt fehlen uns aber noch die Werte für die einzelnen Ströme (Teilströme) durch den Widerstand, die Spule und den Kondensator.

Wir rechnen hier mit den Effektivwerten weiter!

Teilströme durch den Ohmschen Widerstand

$\boxed{I_R = \frac{U}{R}}$

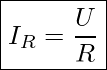
Teilströme durch die Spule (Induktivität)

$\boxed{I_L = \frac{U}{\omega \cdot L }}$

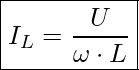
Teilströme durch den Kondensator (Kapazität)

$\boxed{ I_C = U \cdot \omega \cdot C }$

Netzstrom aus Stromdreieck

In der Vergangenheit konnten wir immer direkt mit der Anwendung des Satz des Pythagoras bei Spannungsdreiecken starten.

Dies geht hier aufgrund der Strecke von $\underline{I}_C$ hier nicht mehr ohne weiteres.

Um dem Problem Herr zu werden, subtrahieren wir $\underline{I}_C$ in Form von $I_C$ (Effektivwert) aus der Gleichung. Das hat den Vorteil, dass auch die zu lang geratene Strecke $\underline{I}_L$ korrekt verkürzt wird und wir den Satz des Pythagoras anwenden können.

Es gilt also:

$\boxed{ I = \sqrt{ I_R^2 + (I_L - I_C)^2} }$

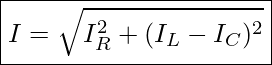
Wenn wir uns jedoch den Netzstrom mit den Werten aus den Stromgleichungen ermitteln möchten, dann sieht das wie folgt aus:

$\boxed{I = \sqrt{(\frac{U}{R})^2 ( \frac{U}{\omega \cdot L} - U \cdot \omega \cdot C)^2} }$

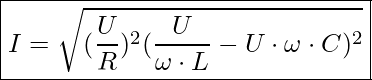
Parallelschwingkreise – Berechnung des Phasenverschiebungswinkels

Den Phasenverschiebungswinkel können wir ganz einfach aus dem Zeigerdiagramm (Rechtwinkligen Stromdreieck ) ermitteln.

$\boxed{tan \varphi = \frac{I_L - I_C}{I_R} }$

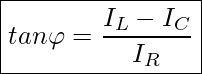
oder mit den Werten aus den Stromgleichungen

$\boxed{tan \varphi = \frac{ \frac{1}{\omega \cdot L} - \omega \cdot C}{\frac{1}{R}} }$

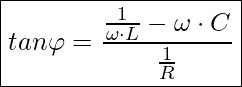
Parallelschwingkreise – Berechnung der Resonanz

Aus unseren bisherigen Gleichungen für die Ströme und den Phasenverschiebungswinkel können wir ableiten, dass der Netzstrom $I$ bei der gegebenen Netzspannung $U$ und einem vorliegenden Widerstand $R$ infolge der Parallelresonanz minimal wird.

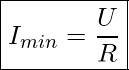$\boxed{I_{min} = \frac{U}{R} }$ – Thomsonsche Formel für Parallelschwingkreise | Minimalwert

Dies setzt jedoch voraus, dass $U_L$ und $U_C$ identisch sind und sich damit in der Berechnung gegenseitig aufheben:

$\boxed{ \frac{1}{ \omega \cdot L} -\omega \cdot C = 0}$

Merk’s dir!

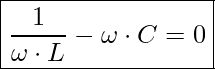
Bei einem mit $L$ und $C$ gleich dimensionierten Reihen- und Parallelschwingkreis hat dieselbe Resonanzfrequenz. Das bedeutet, dass die Thomsonsche Schwingungsformel zur Berechnung unverändert für beide bleibt.

Darstellung der Parallelresonanz (Resonanz) im Zeigerbild

Zum Abschluss dieser Lerneinheit stellen wir noch eben schnell das Zeigerbild für die Parallelresonanz, besser gesagt von dessen Wirkung.

Parallelresonanz - Schwingkreis — Parallelresonanz – Schwingkreis

Wie in der Letzten Gleichung schon ersichtlich wurde, heben sich die beiden Teilströme $\underline{I}_L$ und $\underline{I}_C$ gegenseitig auf.

Daraus leiten wir folgenden Zusammenhänge im Zeigerdiagramm ab:

$\boxed{ \underline{I}_L = - \underline{I}_C }$

das bedeutet

$\boxed{ \underline{I} = \underline{I}_R }$

Bei den Effektivwerten haben wir folgenden Zusammenhang:

$\boxed{ I_L = I_C }$