[INFO3] PH2 – Kräftezerlegung (inkl. Video)
Dieser Kurstext ist ein Auszug aus unserem Onlinekurs: PH2 – Einführung in die Statik
In dieser Lektion schauen wir uns die Zerlegung einer Kraft in zwei Kraftkomponenten an. Dieses Vorgehen bezeichnet der Techniker auch als Kräftezerlegung bzw. Zerlegung einer Kraft.
Unter der Kräftezerlegung versteht man, die Zerlegung einer einzelnen Kraft in mindestens zwei Teilkräfte, die in unterschiedlichen Richtungen wirken.
Die Kräftezerlegung ist für spätere Berechnungen und für deiner Prüfung sehr wichtig. Deswegen ist es notwendig, dass du diese Methode sicher beherrschst.
Schauen wir uns nun an, wie du eine Kraft in zwei Kräfte zerlegst. Die beiden Kräfte ersetzen dabei die gegebene Kraft. Stellen dir dazu eine Kiste vor, an welche eine Kraft F angreift:
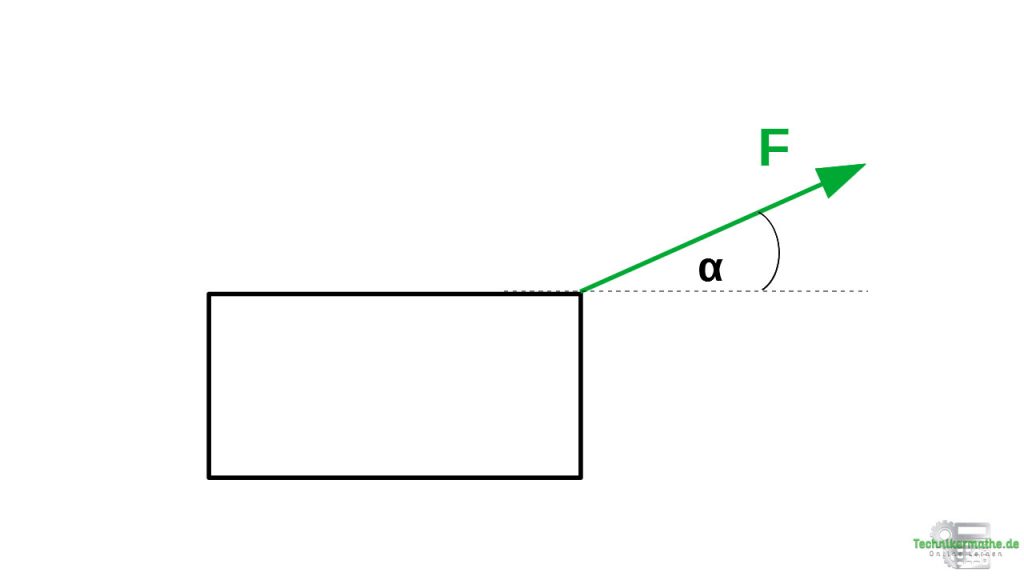
Auf die obige Kiste wirkt die Kraft F mit einem Winkel α zur Horizontalen (gestrichelte Linie). Für die analytische Berechnung muss immer der Winkel von der gegebenen Kraft zur Horizontalen oder zur Vertikalen gegeben sein, damit die Kräftezerlegung durchgeführt werden kann.
Vorgehensweise: Kräftezerlegung
Schritt 1: Gegebene Kraft mit Anfangspunkt in ein x,y-Koordinatensystem legen. Gegebenenfalls Winkel zur x-Achse bestimmen.
Schritt 2: Unter Anwendung von Sinus und Kosinus wird die gegebene Kraft in eine Kraftkomponente in x-Richtung und in y-Richtung zerlegt.
Schritt 3: Die beiden berechneten Kräfte ersetzen die alte Kraft.
Schritt 1: Koordinatensystem
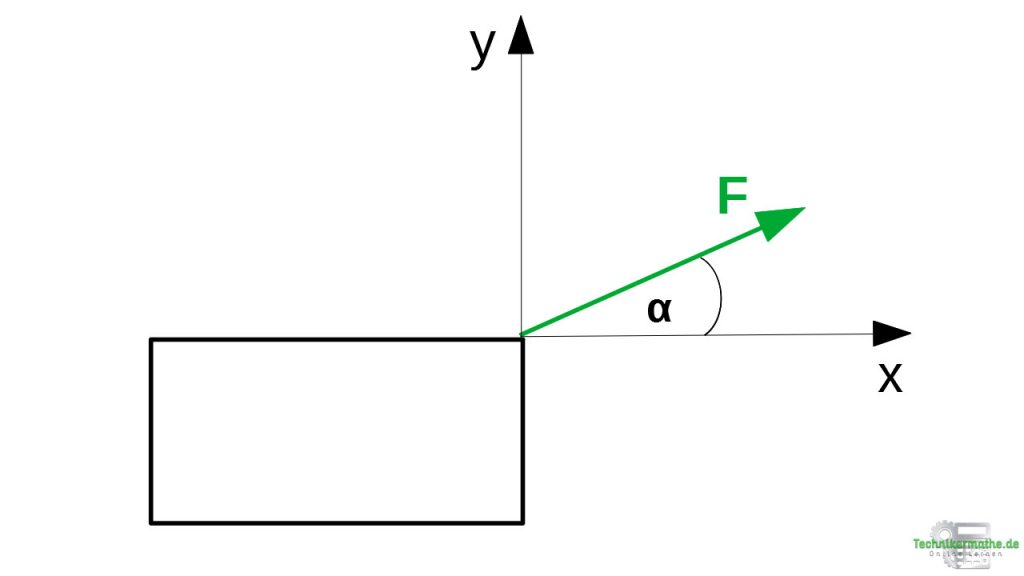
Die gegebene Kraft wird mit ihrem Anfangspunkt in den Koordinatenursprung gelegt. Dabei wird der Winkel mit eingezeichnet. Ist der Winkel zur Vertikalen gegeben, so kannst du den Winkel zur Horizontalen einfach berechnen, indem du diesen von 90° abziehst.
Schritt 2: Kräftezerlegung
Im 2. Schritt geht es um die eigentliche Kräftezerlegung. Wir wollen die gegebene Kraft in die beiden Kräfte Fx (in x-Richtung) und Fy (in y-Richtung) zerlegen:
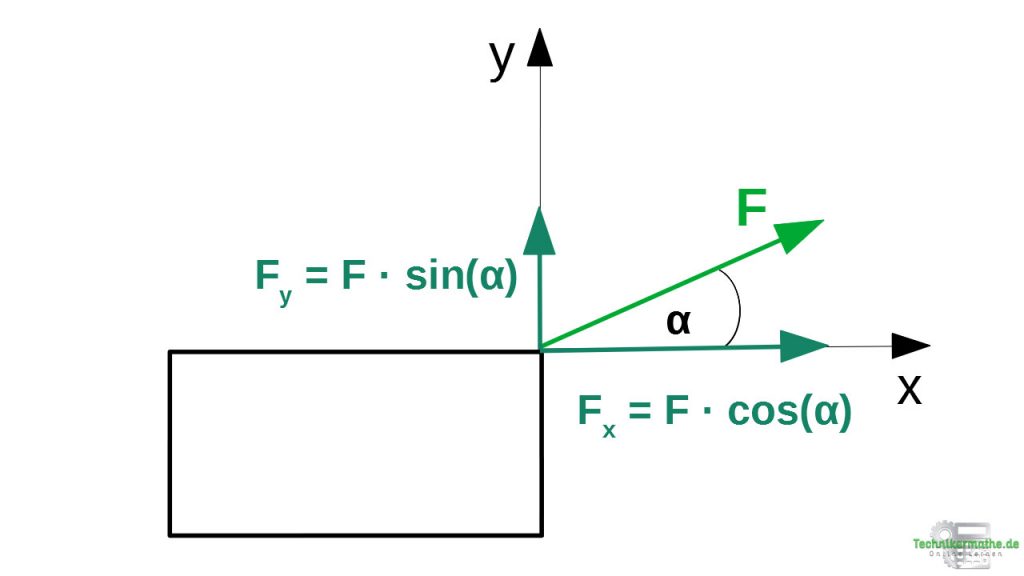
Hierfür benötigen wir den Sinus und den Kosinus des gegebenen Winkels. Dabei gilt:
- Ist der eingeschlossene Winkel von der Kraft zur x-Achse gegeben, so ist
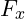die Ankathete und wird mittels Kosinus berechnet. In diesem Fall wird 
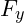mittels Sinus berechnet. - Ist der eingeschlossene Winkel von der Kraft zur y-Achse gegeben, so ist 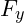die Ankathete und wird mittels Kosinus berechnet. In diesem Fall wird 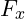mittels Sinus berechnet.
Merk dir Fall 1 und berechne immer den Winkel von der gegebenen Kraft F zur x-Achse. So kannst du die Kräftezerlegung immer wie folgt durchführen:
Schritt 3: Kraft ersetzen
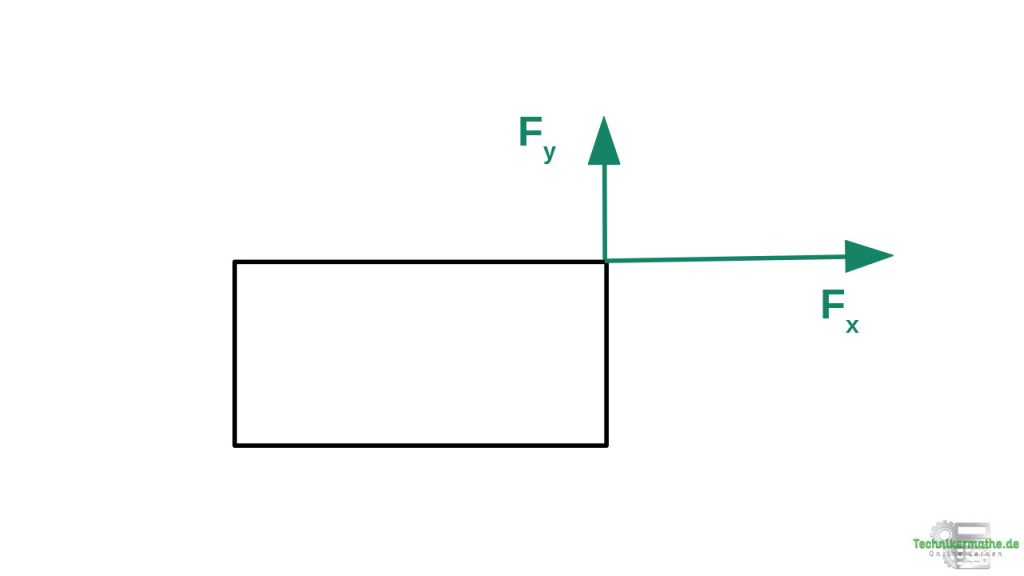
In der obigen Grafik haben wir die Kraft F durch ihre beiden Komponenten ersetzt. Die beiden Kräfte 
und 
üben dieselbe Wirkung auf die Kiste aus, wie die beiden Kräfte zusammen.
Bei der späteren Berechnung der Auflagerkräfte musst du wissen, wie eine Kraft in ihre zwei Komponenten zerlegt wird. Ist also in der Aufgabenstellung eine Kraft mit Winkel gegeben, so musst du diese zunächst in ihre beiden Komponenten zerlegen. Anstelle der Kraft mit dem Winkel zeichnest du dann die beiden berechneten Kräfte ein, die du dann innerhalb der Gleichgewichtsbedingungen berücksichtigen kannst. Dieses Vorgehen zeigen wir dir aber noch ausführlich innerhalb der Berechnungen von Lagerkräften.
Schauen wir uns dazu mal ein Beispiel zur Kräftezerlegung an.
Beispiel: Kräftezerlegung
Im folgenden Beispiel lernst du, wie du eine Kraft in ihre beiden Komponenten zerlegst:
Beispiel 1: Zerlegung einer Kraft im 2. Quadranten
Beispiel 2: Zerlegung einer Kraft im 1. Quadranten
Beispiel 1: Zerlegung einer Kraft im 2. Quadranten
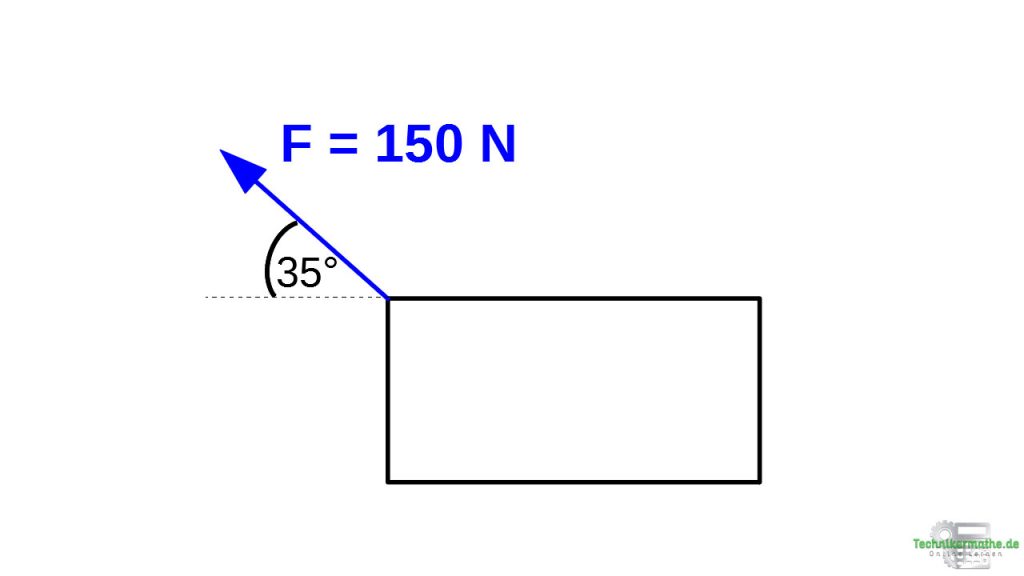
Gegeben sei eine Kiste, an welche die Kraft F = 150 N mit einem Winkel von 35° zur Horizontalen angreift.
Führe eine Kräftezerlegung durch!
1.Schritt: Koordinatensystem
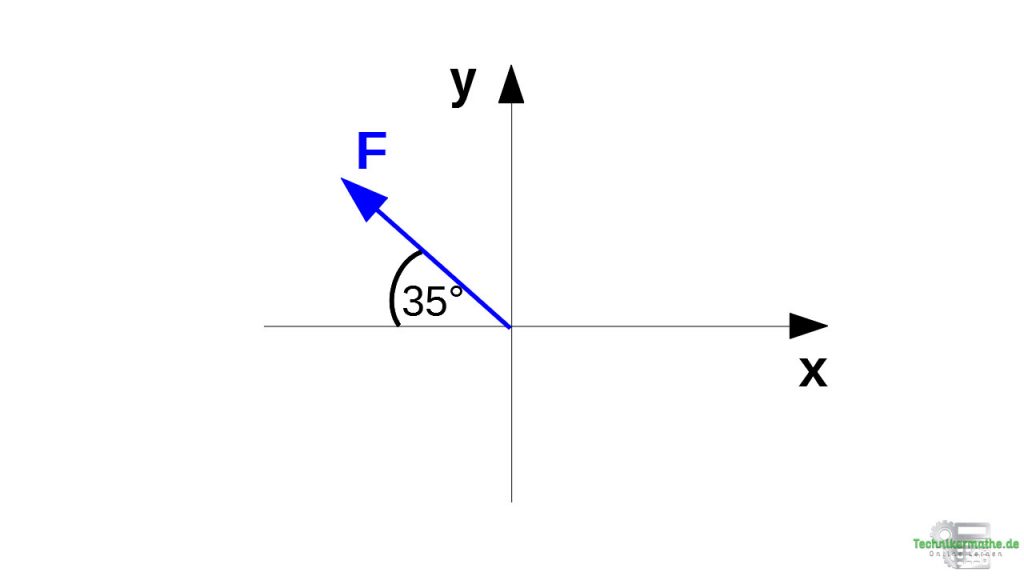
Zunächst wird die Kraft mit dem Anfangspunkt in das Koordinatensystem legen. Die Kraft befindet sich im 2. Quadranten des Koordinatensystems (siehe Grafik).
2.Schritt: Kraftkomponenten berechnen
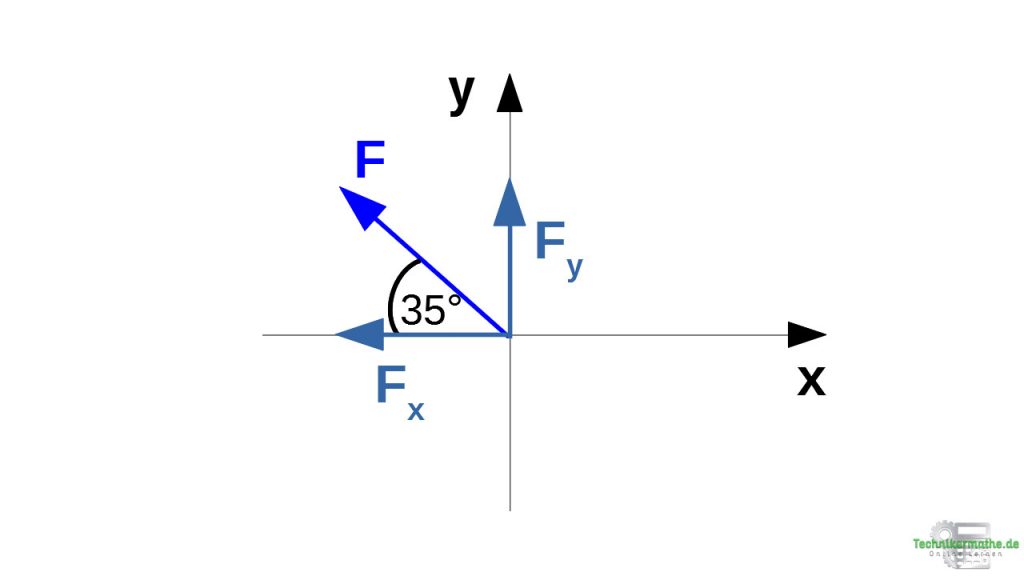
Da der Winkel zur x-Achse gegeben ist, ist Fx die Ankathete und wird mit dem Kosinus berechnet. Fy wird somit mit dem Sinus berechnet:
Die Kraftkomponente Fx ist größer als Fy. Das liegt daran, weil die gegebene Kraft F näher an der x-Achse liegt als an der y-Achse. Damit ist die Wirkung in x-Richtung größer als in y-Richtung.
3.Schritt: Kraft ersetzen
Im dritten und letzten Schritt wird die Kraft F durch die beiden berechneten Kraftkomponenten ersetzt. Diese üben dieselbe Wirkung auf die Kiste aus.
Beispiel 2 : Zerlegung einer Kraft im 1. Quadranten
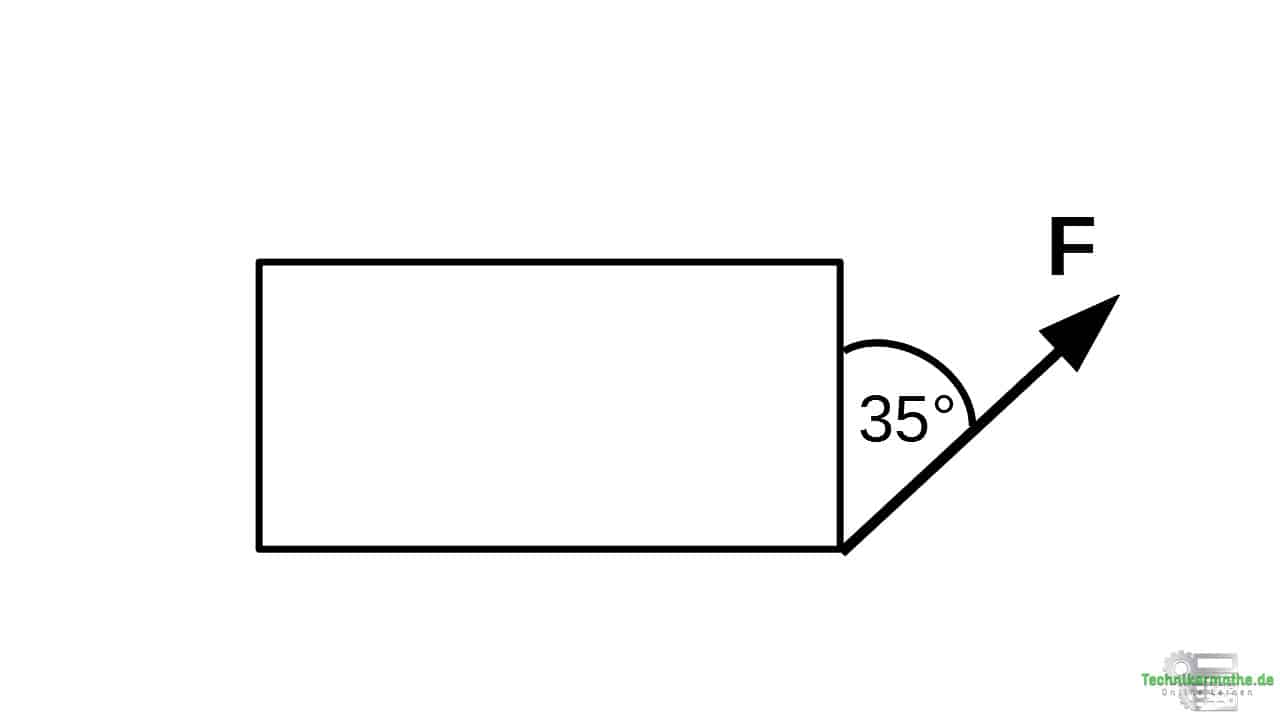
Gegeben sei die obige Kiste, an welche die Kraft F = 100 N angreift.
Führe eine Kräftezerlegung durch!
1.Schritt: Koordinatensystem
Zunächst legen wir die Kraft F mit dem Anfangspunkt in den Koordinatenursprung. Die Kraft F liegt im 1. Quadranten.
Gegeben ist der Winkel von der Kraft F zur Vertikalen mit 35°. Wir berechnen den Winkel zur Horizontalen:
2.Schritt: Komponenten berechnen
Jetzt können wir die x-Komponente mit dem Kosinus berechnen und die y-Komponente mit dem Sinus.
3.Schritt: Kraft F ersetzen
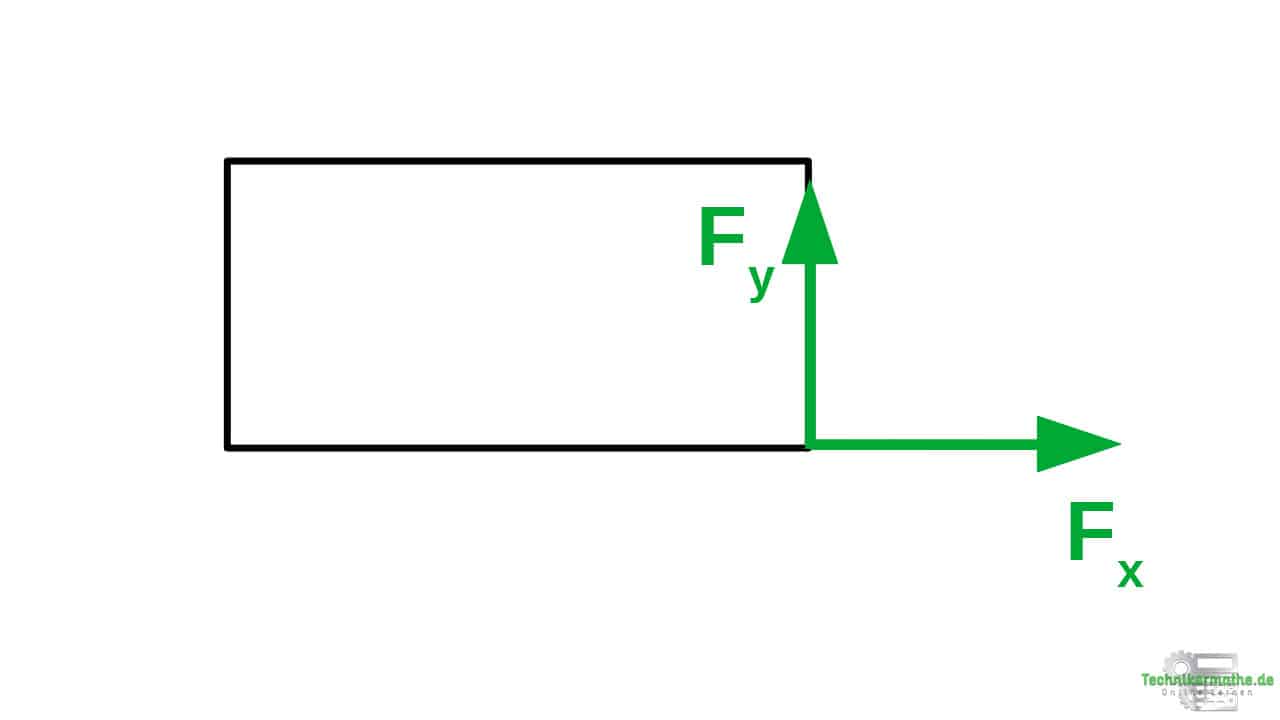
Wir ersetzen nun die Kraft F durch ihre beiden Komponenten.
Videoclip: Kräftezerlegung
Im folgenden Video schauen wir uns die Kräftezerlegung an. Jessica erklärt dir ganz einfach, wie du hier vorgehen musst.