Neue Themen, Kurse und Webinare!

Guten Morgen zusammen,

ich hoffe ihr hattet alle ein schönes Wochenende. Schauen wir uns mal an, was genau dazu gekommen ist und was euch in der nächsten Zeit erwartet.

Neue Themen & neuer Kurs

In der letzten Woche sind neue Themen in unseren Kursen TM1 und PH2 hinzugekommen sowie der Onlinekurs Geometrische Körper.

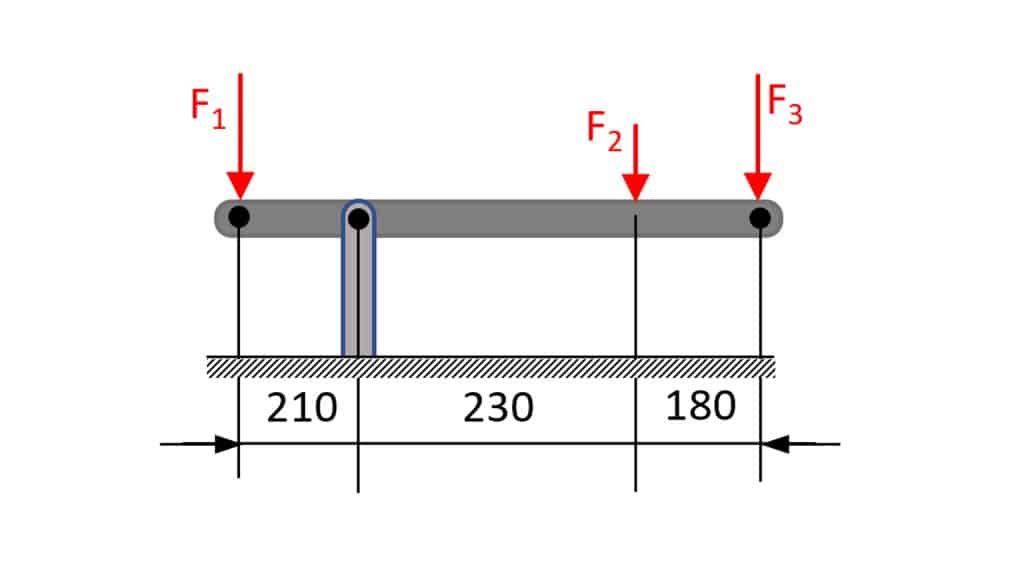
Zunächst einmal findet ihr in unserem Onlinekurs TM1-Statik das neue Thema >>Schnittgrößen am Rahmen<<. Hier zeigen wir euch Schritt für Schritt, wie ihr die Schnittgrößen am Rahmen aus den Gleichgewichtsbedingungen berechnen könnt:

Außerdem findet ihr in unserem Onlinekurs PH2-Einführung in die Statik die neuen Themen zum >>einseitigen und zweiseitigen Hebel<< inklusive Videos:

Neuer Kurs: Kurvendiskussion

Außerdem ist der Onlinekurs [GK] Geometrische Körper jetzt online. Hier könnt ihr euch nochmal anschauen, wie >>Volumen und Oberflächen<< der gängigen geometrischen Körper berechnet werden.

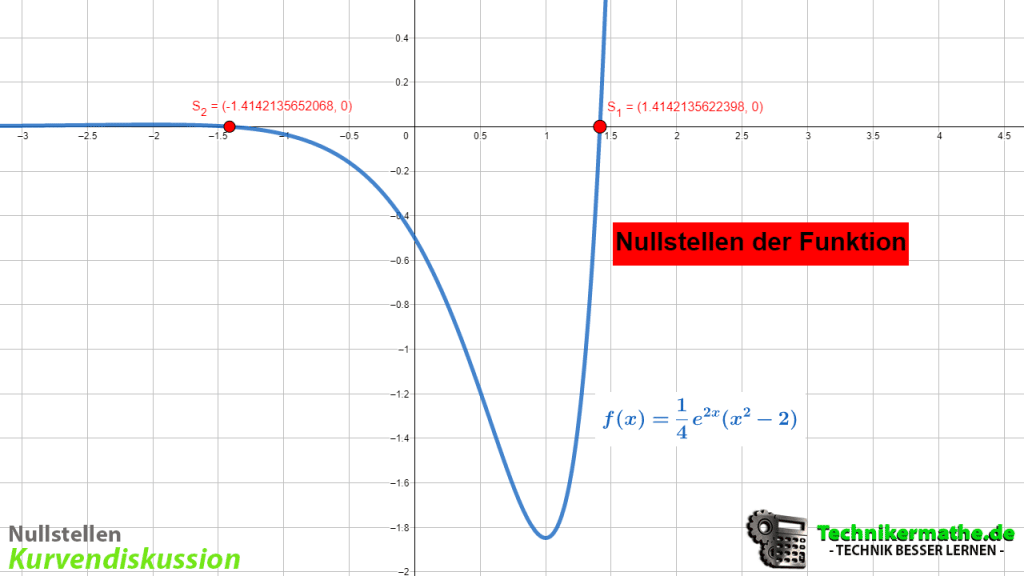
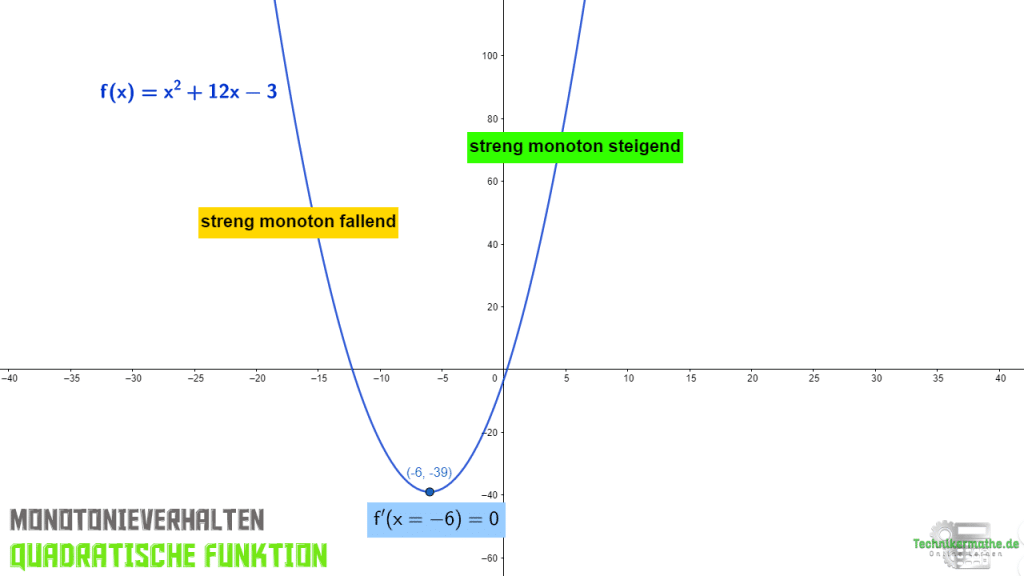
In dieser Woche starten wir mit dem Onlinekurs [MA3] – Kurvendiskussion. Wir starten mit den quadratische Funktionen (x²) und zeigen euch, wie die Kurvendiskussion durchgeführt wird. Folgende Themen werden u.a. behandelt:

• Ableitungen
• Definitionsmenge
• Nullstellen
• Extremwerte (Hoch- und Tiefpunkte)
• Wendepunkte
• Verhalten im Unendlichen

Webinar: Geometrische Grundlagen

Am Dienstag den 17.05.2022 um 18 Uhr findet ein Webinar zu den geometrischen Grundlagen statt. Ich zeige euch hier, wie ihr den Satz des Pythagoras, den Kosinussatz, Sinussatz und die trigonometrischen Funktionen verwendet, um Seiten oder Winkel in einem Dreieck zu bestimmen. Diese Grundlagen sind Grundvoraussetzung für viele Berechnungen innerhalb der Physik. Wollt ihr also wissen wie diese geometrischen Funktionen angewendet werden, so seit auf jeden Fall dabei. 

Das Webinar ist gratis und es entstehen keinerlei Kosten. Das Webinar wird aufgezeichnet und im Kurs PH1 – Geometrische und physikalische Grundlagen zu finden sein.