MA3 – Verhalten im Unendlichen – gebrochenrationale Funktionen

In dieser Kurseinheit betrachten wir das Verhalten im Unendlichen, das Thema ist: Verhalten im Unendlichen bei gebrochenrationalen Funktionen. Somit sei eine gebrochenrationale Funktion gegeben.

Für ein optimales Verständnis helfen dir drei ausführliche Beispiele mit Zahlenwerten zu dem Thema.

Mehr zu diesem Thema und der Mathematik findest du im Kurs: Onlinekurs MA3 – Kurvendiskussion.

Oder lieber mit den Grundlagen starten? Alles dazu findest du im Kurs: Ma1-Grundlagen der Mathematik

Verhalten im Unendlichen – Gebrochenrationale Funktionen | Grundlagen

Das Verhalten einer Funktion im Unendlichen dient dazu, sich das Aussehen bzw. den Verlauf der Funktion bei sehr großen bzw. sehr kleinen x-Werten vorstellen zu können. Was passiert mit der Funktion z.B. bei einem x-Wert von 1.000.000 oder viel höher bzw. -1.000.000 oder viel niedriger? Verläuft die Funktion in positive oder negative y-Richtung? Um eine Aussage darüber treffen zu können, untersuchen wir das Verhalten der Funktionswerte (=y-Werte) für positive und negative x-Werte gegen unendlich (∞).

Verhalten im Unendlichen – Gebrochenrationale Funktionen

Das Verhalten gebrochenrationaler Funktionen im Unendlichen ist ein grundlegendes Konzept in der Mathematik und Analyse. Gebrochenrationale Funktionen sind Verhältnisse zweier Polynome und ihr Verhalten für große positive und negative Werte von $x$ ist entscheidend für das Verständnis ihres Graphen und asymptotischer Eigenschaften.

Grundprinzipien

Definition einer gebrochenrationalen Funktion:
- Eine gebrochenrationale Funktion hat die Form $f(x) = \frac{P(x)}{Q(x)}$ , wobei $P(x)$ und $Q(x)$ Polynome sind und $Q(x) \neq 0$ .
Asymptotisches Verhalten:
- Horizontale Asymptoten: Diese beschreiben das Verhalten der Funktion, wenn 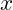$x$ gegen $\pm \infty$ geht.
- Schiefe Asymptoten: Diese treten auf, wenn der Grad des Zählers genau um eins größer ist als der Grad des Nenners.
- Vertikale Asymptoten: Diese treten auf, wenn der Nenner der Funktion bei bestimmten $x$ -Werten Null ist.

Verhalten im Unendlichen – Gebrochenrationale Funktionen | Berechnungen

Lässt man die x-Werte der Funktion f(x) gegen +∞ oder -∞ laufen, lautet die Schreibweise:

Verhalten der Funktion

$\lim \limits_{x \to \infty} f(x)$ Verhalten der Funktion bei x gegen plus unendlich

$\lim \limits_{x \to -\infty} f(x)$ Verhalten der Funktion bei x gegen minus unendlich

Wir wollen im Folgenden das Verhalten im Unendlichen bei gebrochenrationalen Funktionen wie folgt unterscheiden:

Der Grad im Nenner ist größer als der Grad im Zähler.
Der Grad im Zähler ist größer als der Grad im Nenner.
Der Grad im Zähler und der Grad im Nenner sind gleich groß.

Verhalten im Unendlichen bei gebrochenrationalen Funktionen

Grad im Nenner größer als Grad im Zähler

Wir betrachten die folgende gebrochenrationale Funktion:

$f(x) = \frac{x^3 + 2x}{x^4 - 3}$

Der Zählergrad (n = 3) der gebrochenrationalen Funktion ist kleiner, als der Nennergrad (m = 4). Wir wollen das Verhalten im Unendlichen für die gegebene Funktion bestimmen, d.h. wir wollen wissen, wie die Funktion aussieht, wenn sehr große oder sehr kleine Werte für x eingesetzt werden. Dazu setzen wir immer größere Zahlen (10, 100, 1000 etc.) oder immer kleinere Zahlen (-10, -100, -1000 etc.) in die gegebene Funktion ein.

Merk’s dir!

Dadurch, dass der Nennergrad (m = 4) größer ist als der Zählergrad, wird der Nenner schneller wachsen als der Zähler und damit strebt der gesamte Bruch gegen Null.

Schauen wir uns das mal an einem Zahlenbeispiel an. Wir setzen nun x = 100 und x = 1.000 in die Funktion ein:

$f(x = 100) = \frac{100^3 + 2 \cdot 100}{100^4 - 3} = 0,01$

$f(x = 1.000) = \frac{1000^3 + 2 \cdot 1000}{1000^4 - 3} = 0,001$

Je größer die Zahlen werden, desto weiter strebt der Bruch gegen Null. Das bedeutet also, dass sich für x → ∞ (x gegen Unendlich) die gebrochenrationale Funktion immer weiter Null nähert:

$\lim \limits_{x \to \infty} f(x) = \lim \limits_{x \to \infty} \frac{x^3 + 2x}{x^4 - 3} = 0$

Als nächstes betrachten wir den negativen Zahlenbereich und setzen x = -100 und x = -1.000 ein:

$f(x = 100) = \frac{(-100)^3 + 2 \cdot (-100)}{(-100)^4 - 3} = -0,01$

$f(x = 1.000) = \frac{(-1000)^3 + 2 \cdot (-1000)}{(-1000)^4 - 3} = -0,001$

Je kleiner die Zahlen werden, desto weiter strebt der Bruch gegen Null (minus Null ist Null). Das bedeutet also, dass sich für x → -∞ (x gegen minus Unendlich) die gebrochenrationale Funktion immer weiter Null nähert:

$\lim \limits_{x \to -\infty} f(x) = \lim \limits_{x \to -\infty} \frac{x^3 + 2x}{x^4 - 3} = 0$

In der folgenden Grafik siehst du die Funktion eingezeichnet:

Verhalten im Unendlichen, Grenzwerte, Limes, gebrochenrationale Funktion, gebrochen rationale Funktion

Merk’s dir!

Verhalten im unendlichen bei gebrochenrationalen Funktionen:

Ist der Nennergrad (m) größer als der Zählergrad (n), so strebt die gebrochenrationale Funktion für plus und minus Unendlich gegen Null.

Grad im Zähler größer als Grad im Nenner

Wir betrachten die folgende gebrochenrationale Funktion:

$f(x) = \frac{x^3 + 5}{x^2 - 1}$

Der Zählergrad (n = 3) der gebrochenrationalen Funktion ist größer, als der Nennergrad (m = 2). Wir wollen das Verhalten im Unendlichen für die gegebene Funktion bestimmen, d.h. wir wollen wissen, wie die Funktion aussieht, wenn sehr große oder sehr kleine Werte für x eingesetzt werden. Dazu setzen wir immer größere Zahlen (10, 100, 1000 etc.) oder immer kleinere Zahlen (-10, -100, -1000 etc.) in die gegebene Funktion ein.

Merk’s dir!

Dadurch, dass der Zählergrad (n = 3) größer ist als der Nennergrad (m = 2), wird der Zähler schneller wachsen als der Nenner und damit strebt der gesamte Bruch gegen Unendlich.

Schauen wir uns das mal an einem Zahlenbeispiel an. Wir setzen nun x = 100 und x = 1.000 in die Funktion ein:

$f(x = 100) = \frac{100^3 + 5}{100^2 - 1} = 100$

$f(x = 1.000) = \frac{1000^3 + 5}{1000^2 - 1}= 1000$

Je größer die Zahlen werden, desto weiter strebt der Bruch gegen plus Unendlich. Das bedeutet also, dass sich für x → ∞ (x gegen Unendlich) die gebrochen rationale Funktion immer weiter plus Unendlich nähert:

$\lim \limits_{x \to \infty} f(x) = \lim \limits_{x \to \infty} \frac{x^3 + 5}{x^2 - 1} = \infty$

Als nächstes betrachten wir den negativen Zahlenbereich und setzen x = -100 und x = -1.000 ein:

$f(x = 100) = \frac{(-100)^3 + 5}{(-100)^2 - 1} = -100$

$f(x = 1.000) = \frac{(-1000)^3 + 5}{(-1000)^2 - 1}= -1000$

Je kleiner die Zahlen werden, desto weiter strebt der Bruch gegen minus Unendlich. Das bedeutet also, dass sich für x → -∞ (x gegen minus Unendlich) die gebrochenrationale Funktion immer weiter minus Unendlich nähert:

$\lim \limits_{x \to -\infty} f(x) = \lim \limits_{x \to -\infty} \frac{x^3 + 5}{x^2 - 1} = -\infty$

In der folgenden Grafik siehst du die Funktion mit ihrem Verhalten im Unendlichen eingezeichnet:

Merk’s dir!

Verhalten im Unendlichen bei gebrochenrationalen Funktionen:

Ist der Zählergrad (n) größer als der Nennergrad (m), so strebt die gebrochenrationale Funktion für plus und minus Unendlich gegen Unendlich.

Ist der Zählergrad größer als der Nennergrad, so strebt die gebrochenrationale Funktion gegen Unendlich. Sie kann hierbei gegen plus oder minus Unendlich verlaufen. Hier kann man pauschal nicht sagen, dass bei x gegen plus unendlich die Funktion gegen plus oder minus unendlich verläuft. Das ist abhängig von den gegebenen Vorzeichen sowie von den gegebenen Exponenten (gerade oder ungerade). Hier empfehle ich, einfach einen positiven und einen negativen Wert für x einzusetzen (z.B. x = 100 für plus unendlich und x = -100 für minus unendlich) und dann zu schauen, ob das Ergebnis positiv oder negativ wird.

Grad im Zähler gleich Grad im Nenner

Wir betrachten die folgende gebrochenrationale Funktion:

$f(x) = \frac{x^4 + 4x - 1}{x^4 + 3}$

Der Zählergrad (n = 4) der gebrochenrationalen Funktion ist gleich dem Nennergrad (m = 4). Hier ist eine andere Vorgehensweise nötig um den Grenzwert zu berechnen.

Wir gehen hier wie folgt vor:

Die größte Potenz (hier: x⁴) im Nenner und im Zähler ausklammern und kürzen.
Werte für plus unendlich und minus unendlich einsetzen und Verhalten im Unendlichen bestimmen.

Schauen wir uns das mal an einem Beispiel an. Zunächst klammern wir die größte Potenz aus (die Werte innerhalb der Klammer erhältst du, indem du diese durch den ausgeklammerten Wert teilst):

$f(x) = \frac{x^4(1 + \frac{4x}{x^2} - \frac{1}{x^2}}{x^4 (1 + \frac{3}{x^2})}$

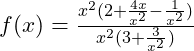
Jetzt kürzen wir x⁴und kürzen im zweiten Bruch x aus dem Zähler:

$f(x) = \frac{1 + \frac{4}{x} - \frac{1}{x^2}}{1 + \frac{3}{x^2}}$

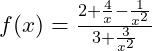
Jetzt müssen wir uns überlegen, wohin Zähler und Nenner streben, wenn wir große positive oder große negative x-Werte einsetzen. Da alle Brüche einen größeren Nennergrad als Zählergrad aufweisen, streben diese Brüche gegen Null:

Verhalten im Unendlichen, gebrochen rationale Funktion, Verhalten im Unendlichen bei gebrochenrationalen Funktionen

In der obigen Grafik siehst du, dass für x →∞ die blau markierten Brüche zu Null werden, da der Nennergrad immer größer ist, als der Zählergrad bzw. im Zähler nur eine Konstante gegeben ist. Damit strebt die Funktion für große positive x-Werte gegen 2/3:

Zähler: $2 + 0 - 0 = 2$

Nenner: $3 + 0 = 3$

Die gebrochenrationale Funktion strebt demnach für x →∞ gegen 2/3:

$\lim \limits_{x \to \infty} f(x) = \lim \limits_{x \to \infty} \frac{x^4 + 4x - 1}{x^4 + 3} = \frac{2}{3}$

Setzen wir für x negative große Werte ein, so streben die Brüche ebenfalls gegen Null und damit die gesamte Funktion gegen 2/3:

$\lim \limits_{x \to -\infty} f(x) = \lim \limits_{x \to -\infty} \frac{x^4 + 4x - 1}{x^4 + 3} = \frac{2}{3}$

In der folgenden Grafik siehst du die Funktion eingezeichnet:

Merk’s dir!

Verhalten im Unendlichen bei gebrochenrationalen Funktionen:

Sind Zählergrad und Nennergrad bei gebrochenrationalen Funktionen gleich, so strebt die Funktion gegen den Quotienten aus den beiden Koeffizienten der größten Zähler- und Nennerpotenz.

Anwendung der Kettenregel

Mathematik: Untersuchung des Graphenverhaltens und der Asymptoten.
Ingenieurwissenschaft: Analyse von Systemen, die durch rationale Funktionen modelliert werden.
Physik: Untersuchung von physikalischen Systemen, die durch gebrochenrationale Funktionen beschrieben werden.

Mögliche Fragestellungen | Häufig gestellte Fragen (FAQs)

1. Was ist eine gebrochenrationale Funktion?

Eine gebrochenrationale Funktion ist das Verhältnis zweier Polynome.

2. Wie findet man horizontale Asymptoten?

Durch Vergleich der Grade des Zähler- und Nennerpolynoms.

3. Wann gibt es schiefe Asymptoten?

Wenn der Grad des Zählers genau um eins größer ist als der Grad des Nenners.

4. Was sind vertikale Asymptoten?

Werte von $x$ , bei denen der Nenner null ist und die Funktion gegen $±∞\pm \infty$ strebt.

5. Warum ist das Verhalten im Unendlichen wichtig?

Es hilft, das Langzeitverhalten und die Struktur des Funktionsgraphen zu verstehen.

Zusammenfassung

Die Bestimmung des Verhaltens gebrochenrationaler Funktionen im Unendlichen ist eine zentrale Technik zur Analyse ihrer Graphen.

Durch die Untersuchung der Grade der Polynome und das Finden von horizontalen, schiefen und vertikalen Asymptoten kann das Verhalten der Funktion für große Werte von $x$ bestimmt werden.

Diese Methode ist in vielen Bereichen wie Mathematik, Ingenieurwissenschaften und Physik von großer Bedeutung und hilft, komplexe Systeme und ihre langfristigen Trends zu verstehen.

Was kommt als Nächstes?

In der folgenden Lerneinheit zeigen wir dir, wie Ableiten mit der Produktregel abläuft.

Was gibt es noch bei uns?

Optimaler Lernerfolg durch tausende Übungsaufgaben

Übungsbereich (Demo) - Lerne mit mehr als 4000 Übungsaufgaben für deine Prüfungen — Übungsbereich (Demo) – Lerne mit mehr als 4000 Übungsaufgaben für deine Prüfungen

Quizfrage 1

Quizfrage 2

“Wusstest du, dass unter jedem Kursabschnitt eine Vielzahl von verschiedenen interaktiven Übungsaufgaben bereitsteht, mit denen du deinen aktuellen Wissensstand überprüfen kannst?”

Alle Technikerschulen im Überblick

Zum Verzeichnis der Technikerschulen (Alles Rund um die Schulen) — Zum Verzeichnis der Technikerschulen

Kennst du eigentlich schon unser großes Technikerschulen-Verzeichnis für alle Bundesländer mit allen wichtigen Informationen (Studiengänge, Kosten, Anschrift, Routenplaner, Social-Media) ? Nein? – Dann schau einfach mal hinein:

Was ist Technikermathe?

Unser Dozent Jan erklärt es dir in nur 2 Minuten!

Oder direkt den > kostenlosen Probekurs < durchstöbern? – Hier findest du Auszüge aus jedem unserer Kurse!

Geballtes Wissen in derzeit 26 Kursen

Hat dir dieses Thema gefallen? – Ja? – Dann schaue dir auch gleich die anderen Themen zu den Kursen

WT3 (Werkstoffprüfung) und
TM1 (Technische Mechanik – Statik) an.

Lerne nun erfolgreich mit unserem Onlinekurs Technische Mechanik 1 — TM1 (Technische Mechanik)

Lerne nun erfolgreich mit unserem Onlinekurs Werkstofftechnik 3 — WT3 (Werkstoffprüfung)

Perfekte Prüfungsvorbereitung für nur 14,90 EUR/Jahr pro Kurs

++ Günstiger geht’s nicht!! ++

Oder direkt Mitglied werden und Zugriff auf alle 26 Kurse (inkl. Webinare + Unterlagen) sichern ab 7,40 EUR/Monat ++ Besser geht’s nicht!! ++

Social Media? - Sind wir dabei!

Kennst du eigentlich schon unseren YouTube-Channel? – Nein? – Dann schau super gerne vorbei:

Technikermathe auf Youtube

Immer auf dem neuesten Stand sein? – Ja? – Dann besuche uns doch auch auf

Technikermathe auf Instagram

Technikermathe auf Facebook

Dein Technikermathe.de-Team

Technikerschulen 2024
(deutschlandweit)

Du bist noch auf der Suche nach der richtigen Schule?

Zum Verzeichnis

< Kostenlos!! >

Wir sind auch auf Youtube!

Wir stellen dir eine große Auswahl von Videos & Webinaren aus allen Kursen vor

Abonniere uns auch gerne

wenn dir unsere Videos gefallen!

Zum YouTube Kanal

Technikermathe.de

"97% unserer Kursnutzer empfehlen uns weiter"

-> 100 % werbefrei
-> Persönliche & direkte Lernbetreuung
-> 100.000 Studenten durch die Prüfungen gebracht
-> Mehr als 11 Jahre Erfahrung
-> Durch Fachexperten geprüfte Inhalte
-> Immer aktuell & täglich Erweiterungen
-> viel günstiger als eine Nachhilfestunde
-> Bestehensgarantie

Jetzt ab 7,40 EUR/Monat perfekt lernen

MA3 – Verhalten im Unendlichen – gebrochenrationale Funktionen

Verhalten im Unendlichen – Gebrochenrationale Funktionen | Grundlagen

Verhalten im Unendlichen – Gebrochenrationale Funktionen

Grundprinzipien

Definition einer gebrochenrationalen Funktion:

Asymptotisches Verhalten:

Verhalten im Unendlichen – Gebrochenrationale Funktionen | Berechnungen

Verhalten im Unendlichen bei gebrochenrationalen Funktionen

Grad im Nenner größer als Grad im Zähler

Grad im Zähler größer als Grad im Nenner

Grad im Zähler gleich Grad im Nenner

Anwendung der Kettenregel

Mögliche Fragestellungen | Häufig gestellte Fragen (FAQs)

Zusammenfassung

Was gibt es noch bei uns?

Optimaler Lernerfolg durch tausende Übungsaufgaben

Alle Technikerschulen im Überblick

Was ist Technikermathe?

Geballtes Wissen in derzeit 26 Kursen

Social Media? - Sind wir dabei!