TM2 – Mohrscher Spannungskreis (Spannungen ablesen) – [Erklärungen, Beispiel, Video]

In dieser Kurseinheit zeigen wir dir, wie du den Mohrschen Spannungskreis aus den gegebenen Spannungen zeichnest und wie du daraus die Hauptnormalspannungen und Hauptschubspannungen ablesen kannst.

Für ein optimales Verständnis helfen dir zwei Videoclips und ein anschauliches Rechenbeispiel zu dem Thema.

Dieser Lerntext ist ein Auszug aus unserem Onlinekurs TM2 – Festigkeitslehre.

Auch interessant! Alles zu Linearen Gleichungssystemen findest du im Kurs: Ma2-Lineare Gleichungssysteme

LernVideos: Zeichnen und Spannungen ablesen

In den folgenden Videos schauen wir uns nochmal im Detail an, wie du den Mohrschen Spannungskreis zeichnest und die Spannungen abliest.

Mohrscher Spannungskreis – Grundlagen

Der Mohrsche Spannungskreis dient der Bestimmung der Extremwerte der Normal- und Schubspannungen, der sogenannten Hauptspannungen sowie der dazugehörigen Hauptrichtungen.

Was ist der Mohrsche Spannungskreis?

Der Mohrsche Spannungskreis ist ein grafisches Werkzeug in der Mechanik und Materialwissenschaft, das zur Bestimmung der Spannungszustände in einem Material verwendet wird. Es hilft Ingenieuren und Wissenschaftlern, die Normal- und Schubspannungen auf verschiedenen Schnittebenen eines Körpers zu visualisieren und zu analysieren.

Grundprinzipien

Definition des Mohrschen Spannungskreises:
- Der Mohrsche Spannungskreis stellt die Beziehung zwischen Normalspannungen 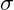$\sigma$ [Sigma] und Schubspannungen 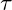$\tau$ [Tau] in einem Material graphisch dar.
- Es ist ein Kreis in einem $\sigma-\tau$ -Diagramm, wobei die Normalspannung auf der horizontalen Achse und die Schubspannung auf der vertikalen Achse aufgetragen wird.
Anwendungsbereiche:
- Bestimmung der Hauptspannungen und Hauptschnittebenen.
- Visualisierung von Spannungszuständen in 2D.
- Analyse von Spannungszuständen in Festkörpern, Bauwerken und Maschinenkomponenten.

Mohrscher Spannungskreis – Anwendungsbereiche

Der Mohr’sche Spannungskreis ist ein grafisches Werkzeug, das in der Festigkeitslehre verwendet wird, um die Spannungszustände in einem Materialpunkt unter verschiedenen Belastungsbedingungen darzustellen. Es bietet eine Möglichkeit, die Hauptspannungen, die Schubspannungen und die resultierenden Spannungen zu visualisieren.

Hier sind einige Anwendungsbereiche für den Mohrschen Spannungskreis:

Festigkeitsanalyse: Der Mohr’sche Spannungskreis wird häufig verwendet, um die Festigkeitseigenschaften eines Materials zu analysieren. Es ermöglicht Ingenieuren, die maximalen und minimalen Spannungen zu bestimmen, denen ein Material unter verschiedenen Belastungsbedingungen ausgesetzt ist. Dies ist wichtig, um die Sicherheit und Zuverlässigkeit von Strukturen und Komponenten zu gewährleisten.
Bestimmung der Bruchfestigkeit: Der Spannungskreis kann verwendet werden, um die Bruchfestigkeit eines Materials zu ermitteln. Durch den Vergleich der tatsächlichen Spannungszustände mit der Bruchfestigkeit kann festgestellt werden, ob ein Material unter den gegebenen Belastungen versagt oder nicht.
Bemessung von Bauteilen: Bei der Konstruktion von Bauteilen ist es wichtig, deren Festigkeit und Tragfähigkeit zu gewährleisten. Der Mohrsche Spannungskreis kann dabei helfen, die Spannungsverteilung und den kritischen Punkt in einem Bauteil zu bestimmen. Dies ermöglicht eine präzise Auslegung und Dimensionierung des Bauteils, um Versagen oder Überbeanspruchung zu vermeiden.
Bodenmechanik: In der Geotechnik wird der Mohrsche Spannungskreis verwendet, um die Spannungsverteilung und die Scherfestigkeit von Bodenproben zu analysieren. Dies ist wichtig, um das Tragverhalten von Fundamenten, Böschungen oder Stützmauern zu verstehen und geeignete Sicherheitsfaktoren anzuwenden.
Materialprüfung: Der Spannungskreis kann auch in Verbindung mit Materialprüfungen eingesetzt werden, um die mechanischen Eigenschaften von Werkstoffen zu charakterisieren. Durch die Analyse der Spannungs-Dehnungs-Diagramme und die Verwendung des Mohrschen Spannungskreises können Ingenieure Informationen über die Elastizität, den Bruchpunkt und andere wichtige Materialeigenschaften gewinnen.

Diese Beispiele zeigen, dass der Mohr’sche Spannungskreis ein leistungsfähiges Werkzeug ist, um Spannungszustände in verschiedenen Anwendungsbereichen der Ingenieurwissenschaften zu analysieren und zu verstehen.

Mohrscher Spannungskreis – Beispiele

Hier sind einige Beispiele für den Mohrschen Spannungskreis:

Eindimensionaler Spannungszustand: In diesem einfachsten Fall gibt es nur eine Normalspannung entlang einer Achse. Der Mohr’sche Spannungskreis reduziert sich auf einen Punkt auf der Achse, da es keine Schubspannungen gibt.
Zweidimensionaler Spannungszustand: Ein Beispiel dafür ist ein uniaxialer Zug- oder Druckversuch. Hier gibt es eine Normalspannung entlang einer Achse und keine Normalspannung in der senkrechten Richtung. Der Mohr’sche Spannungskreis wird als horizontaler Punkt auf der Achse dargestellt.
Reiner Scherzustand: In diesem Fall gibt es nur Schubspannungen, und keine Normalspannungen sind vorhanden. Der Mohr’sche Spannungskreis besteht aus einem Kreis mit dem Mittelpunkt auf der Schubspannungsachse.
Biaxialer Spannungszustand: Ein Beispiel ist der Spannungszustand in einem dünnen, flachen Stab, der an den Rändern gehalten wird und axial gezogen oder gedrückt wird. Der Mohr’sche Spannungskreis besteht aus einem Kreis mit dem Mittelpunkt auf der Achse der größten Normalspannung und dem Radius, der den Unterschied zwischen den beiden Hauptspannungen darstellt.
Triaxialer Spannungszustand: Ein Beispiel dafür ist der Spannungszustand in einem eingespannten zylindrischen Druckbehälter. Der Mohr’sche Spannungskreis besteht aus einem Kreis mit dem Mittelpunkt auf der Achse der größten Normalspannung und dem Radius, der den Unterschied zwischen der größten und der kleinsten Hauptspannung darstellt.

Beispiel: Zeichnen und Spannungen ablesen

Gegeben sei uns der folgende Spannungszustand:

$\sigma_x = 40 MPa$

$\sigma_y = -25 MPa$

$\tau_{xy} = -12 MPa$

Koordinatensystem festlegen und Punkte einzeichnen

Schritt 1: Zunächst zeichnest du ein σ,τ-Koordinatensystem (die σ-Achse ist die Abszisse und die τ-Achse die Ordinate).

Schritt 2: Als nächstes werden die Punkte $P_1(\sigma_x | \tau_{xy})$ und $P_2(\sigma_x | - \tau_{xy})$ abgetragen und miteinander verbunden.

Bei der Festlegung des Koordinatensystems sollte der Maßstab sinnvoll gewählt werden. Nicht zu klein, weil sonst die Spannungen nicht genau abgelesen werden können und auch nicht zu groß, so dass der Spannungskreis noch auf das Zeichenblatt passt.

Für unser Beispiel werden die beiden Punkte $P_1(40|-12)$ und $P_2(-25| -(-12)) = P_2(-25|12)$ abgetragen und miteinander verbunden:

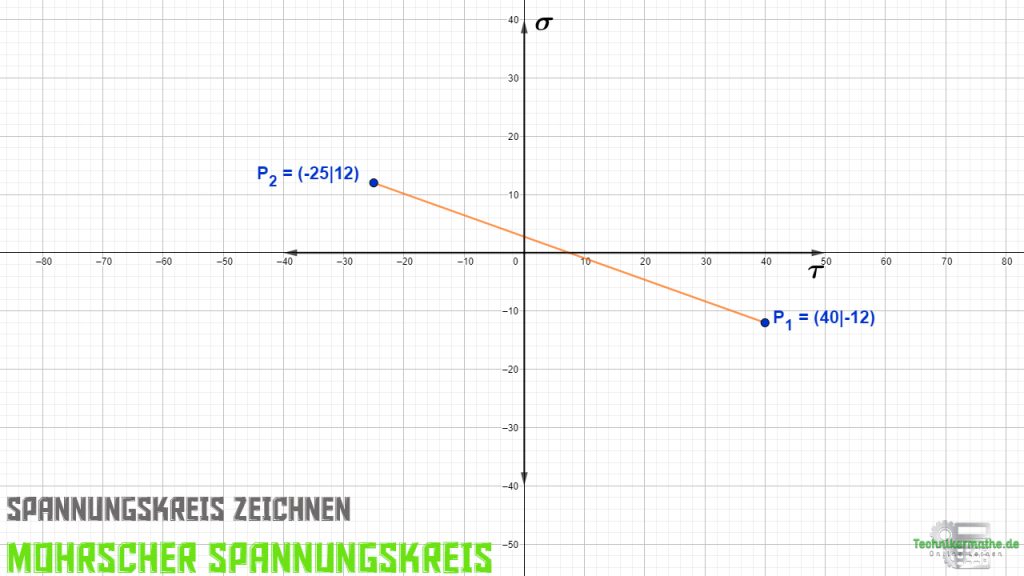
Mohrscher Spannungskreis, Beispiel, Zeichnen, Mohrschen Spannungskreis zeichnen — Mohrscher Spannungskreis – Einzeichnen der gegebenen Spannungen

Kreismittelpunkt festlegen

Schritt 3: Der Kreismittelpunkt liegt im Schnittpunkt der Verbindungslinie mit der σ-Achse. Hier ist auch gleichzeitig die mittlere Normalspannung σ_M gegeben.

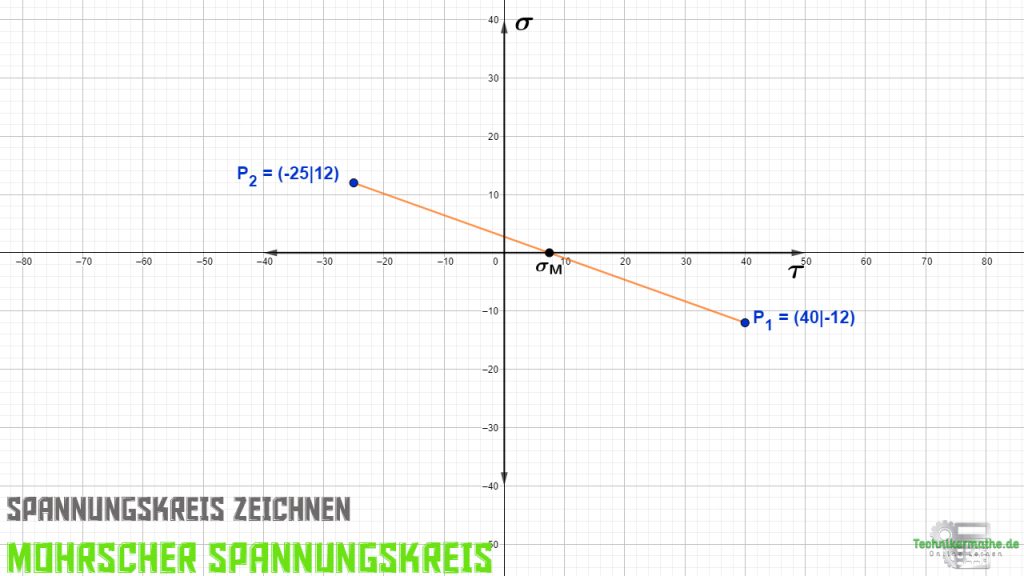
Kreis zeichnen

Schritt 4: Der Kreis verläuft durch die beiden Punkte P₁ und P₂.

Zum Zeichnen des Kreises wird ein Zirkel benötigt. Dieser wird im Kreismittelpunkt (bei der mittleren Normalspannung $\sigma_M$ ) angesetzt. Es wird dann ein Kreis durch die beide Punkte P₁ und P₂ gezogen.

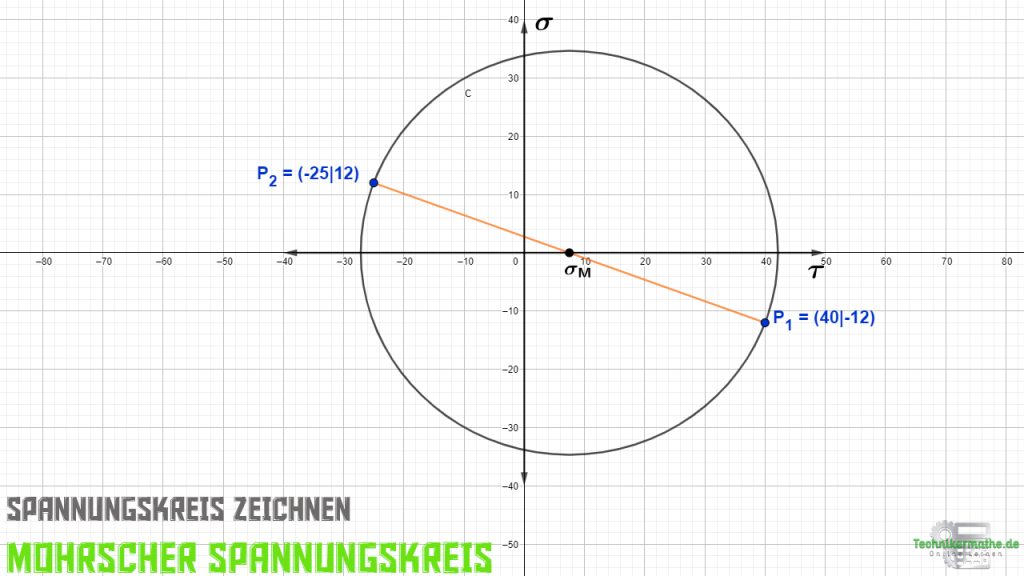
Mohrscher Spannungskreis, Festigkeitslehre, Techniker Nachhilfe, Spannungskreis zeichnen, — Spannungskreis zeichnen

Mohrscher Spannungskreis: Spannungen ablesen

Nachdem wir den Mohrschen Spannungskreis gezeichnet haben, wollen wir als nächstes die Spannungen und Winkel ablesen.

Mittlere Normalspannung

Die erste Spannung, die wir bereits vor dem Zeichnen des Kreises ablesen können, ist die mittlere Normalspannung σ_M, die sich aus dem Schnittpunkt der Verbindungslinie mit der σ-Achse ergibt:

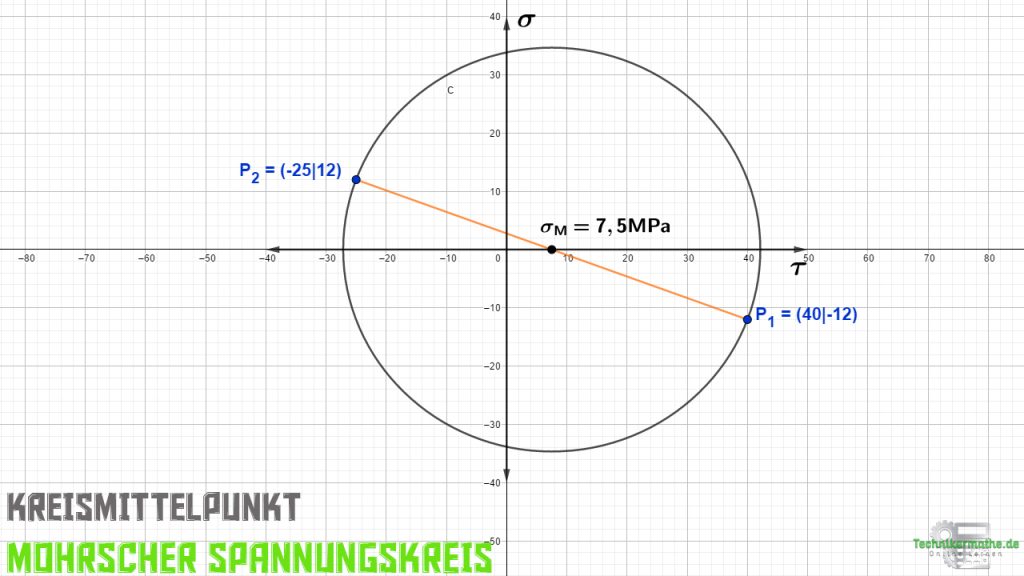
Die mittlere Normalspannung liegt genau im Kreismittelpunkt. In unserem Beispiel beträgt die mittlere Normalspannung:

$\sigma_M = 7,5 MPa$

Merk’s dir!

Aus der vorherigen Lektion weißt du bereits, dass die mittlere Normalspannung dann auftritt, wenn die Schubspannungen ihre Extremwerte annehmen (Hauptschubspannungen).

Du kannst auch jederzeit überprüfen, ob der Wert, den du abgelesen hast richtig ist, indem du einfach die mittlere Normalspannung mittels der folgenden Formel berechnest:

$\sigma_M = \dfrac{\sigma_x + \sigma_y}{2}$

Einsetzen der Werte ergibt:

$\sigma_M = \dfrac{40 MPa + (-25 MPa)}{2} = 7,5 MPa$

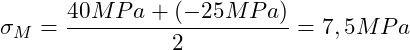
Hauptnormalspannungen

Treten die Hauptnormalspannungen (Extremwerte der Normalspannungen) auf, dann verschwinden die Schubspannungen. Mit diesem Wissen können wir die Hauptnormalspannungen ganz einfach ablesen. Sie befinden sich am Rand des Mohrschen Spannungskreises auf der σ-Achse:

Merk’s dir!

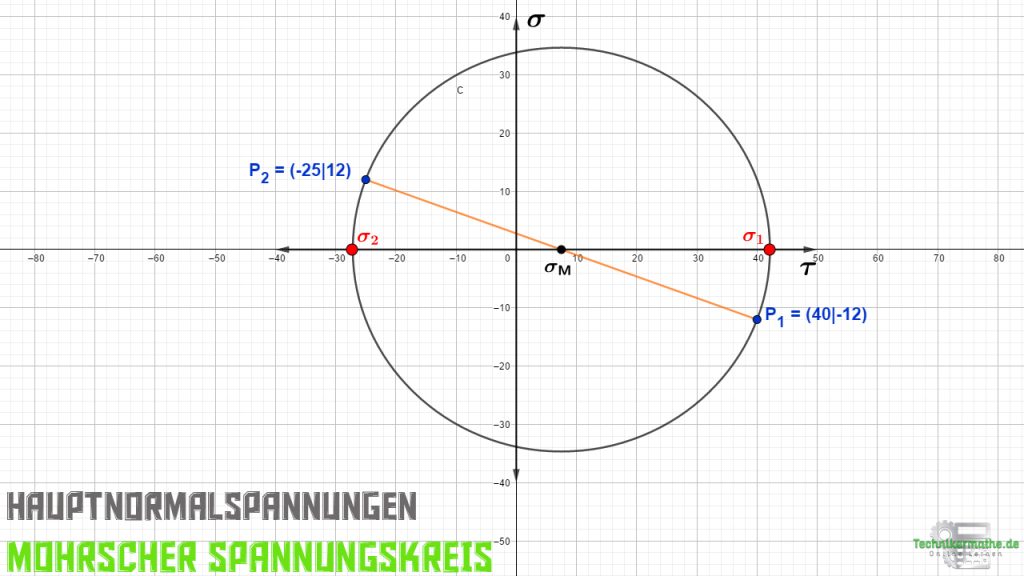
Wichtig: Die Hauptnormalspannung σ₁ ist immer größer als die Hauptnormalspannung σ₂. Somit liegt σ₁ immer rechts von σ₂.

Wir lesen die obigen Werte ab und erhalten in etwa:

$\sigma_1 = 42 MPa$

$\sigma_2 = -27 MPa$

Du kannst auch jederzeit überprüfen, ob der Wert, den du abgelesen hast richtig ist, indem du die Hauptnormalspannungen mittels der folgenden Formel berechnest:

$\sigma_{1} = \dfrac{\sigma_x + \sigma_y}{2} + \sqrt{\dfrac{\sigma_x - \sigma_y}{2})^2 + \tau_{xy}^2}$

$\sigma_{2} = \dfrac{\sigma_x + \sigma_y}{2} - \sqrt{\dfrac{\sigma_x - \sigma_y}{2})^2 + \tau_{xy}^2}$

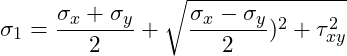
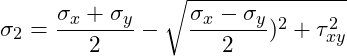
Einsetzen der Werte ergibt:

$\sigma_{1} = \dfrac{40 MPa + (-25 MPa)}{2} + \sqrt{\dfrac{40 MPa - (-25 MPa)}{2})^2 + (-12 MPa)^2} = 42,14 MPa$

$\sigma_{2} = \dfrac{40 MPa + (-25 MPa)}{2} - \sqrt{\dfrac{40 MPa - (-25 MPa)}{2})^2 + (-12 MPa)^2} = -27,14 MPa$

Hauptschubspannungen

Treten die Hauptschubspannungen auf, so nehmen die Normalspannungen ihren mittleren Wert an. Du ziehst also eine Hilfslinie ausgehend von der mittleren Normalspannung σ_M (=Kreismittelpunkt) in positive und negative τ-Richtung bis zum Rand des Mohrschen Spannungskreises. Dort liegt die maximale und minimale Hauptschubspannung:

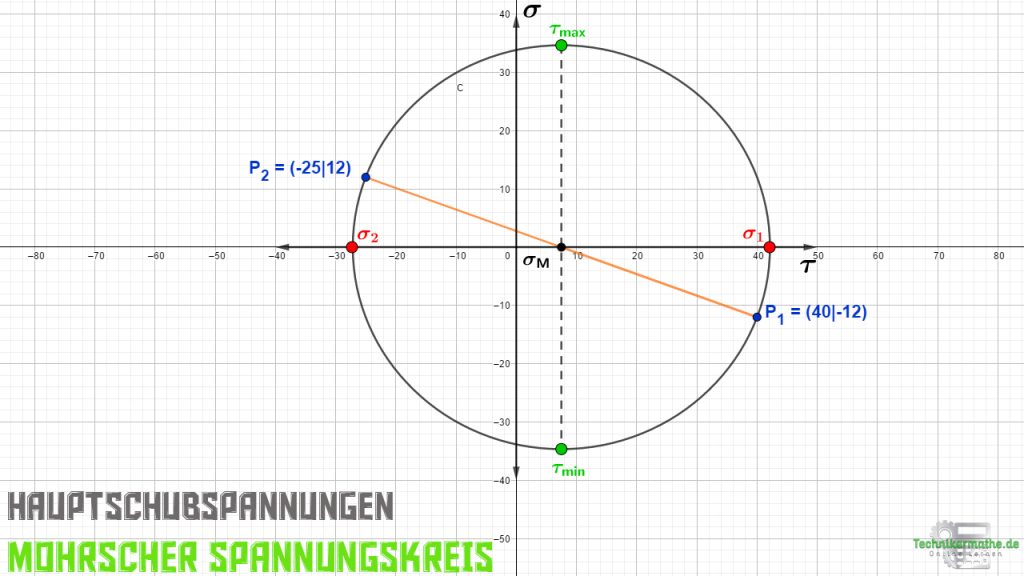
Wir lesen die obigen Werte ab und erhalten in etwa:

$\sigma_{max} = 35 MPa$

$\sigma_{min} = -35 MPa$

Du kannst auch jederzeit überprüfen, ob der Wert, den du abgelesen hast richtig ist, indem du die Hauptnormalspannungen mittels der folgenden Formel berechnest:

$\tau_{min} = \sqrt{(\dfrac{\sigma_x - \sigma_y}{2})^2 + \tau_{xy}^2} = -\tau_{max}$

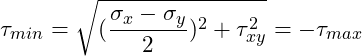
Einsetzen der Werte:

$\tau_{max} = \sqrt{(\dfrac{40 MPa - (-25 MPa)}{2})^2 + (-12 MPa)^2} = 34,64 MPa$

$\tau_{min} = -\tau_{max} = - 34,64 MPa$

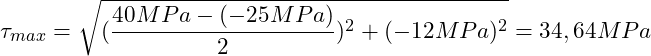
Mohrscher Spannungskreis in 3D

Normalerweise wird der Mohrsche Spannungskreis in einer zweidimensionalen Ebene dargestellt. Allerdings kann er auch auf den dreidimensionalen Fall erweitert werden, um Spannungen in einem Material vollständiger zu beschreiben. Die dreidimensionale Realität kann man mit 3 Mohr’schen Spannungskreisen darstellen.

Merk’s dir!

In einem 3D-Mohrschen Spannungskreis werden die drei Hauptspannungen eines Materials in einem dreidimensionalen Koordinatensystem dargestellt. Diese Hauptspannungen sind die Normalspannungen entlang der Hauptachsen des Koordinatensystems. Der Koordinatenursprung repräsentiert den Spannungszustand, bei dem alle Hauptspannungen null sind.

Der Spannungszustand wird durch einen Punkt im dreidimensionalen Raum dargestellt. Die Koordinaten dieses Punktes entsprechen den drei Hauptspannungen. Die Position dieses Punktes im Raum zeigt an, wie sich die Spannungen im Material verteilen.

Zusätzlich zu den Hauptspannungen kann der 3D-Mohrsche Spannungskreis auch Schubspannungen berücksichtigen. Schubspannungen treten entlang der Schubebenen auf und sind für die Festigkeitsanalyse von Materialien von Bedeutung.

Die Konstruktion des 3D-Mohrschen Spannungskreises erfolgt ähnlich wie in der 2D-Version. Durch die Rotation des 2D-Spannungskreises um eine Achse können verschiedene Schnittebenen erstellt werden, die die Verteilung der Spannungen in verschiedenen Richtungen zeigen.

Anwendung des senkrechten Wurfes nach oben

Ingenieurwesen: Analyse der Belastung von Brücken, Gebäuden und Maschinenkomponenten.
Materialwissenschaft: Untersuchung von Spannungen in Werkstoffen und Bauteilen.
Geotechnik: Bestimmung der Spannungen im Boden und Fels.

Mögliche Fragestellungen | Häufig gestellte Fragen (FAQs)

1. Was ist der Mohrsche Spannungskreis?

Der Mohrsche Spannungskreis ist eine grafische Darstellung, die die Normal- und Schubspannungen auf verschiedenen Schnittebenen eines Körpers zeigt.

2. Wie wird der Mohrsche Spannungskreis konstruiert?

Durch Berechnung der Mittelspannung und des Radius, gefolgt von der Darstellung dieser Werte in einem $σ\sigma$ – $τ\tau$ -Diagramm.

3. Welche Informationen liefert der Mohrsche Spannungskreis?

Er liefert die Hauptspannungen, die maximale Schubspannung und die Orientierung der Hauptschnittebenen.

4. Warum ist der Mohrsche Spannungskreis wichtig?

Er ermöglicht eine umfassende Analyse des Spannungszustandes in Materialien und Konstruktionen, was für die Festigkeitsanalyse und das Design von großer Bedeutung ist.

5. Kann der Mohrsche Spannungskreis für dreidimensionale Spannungszustände verwendet werden?

Ja, aber es erfordert die Konstruktion mehrerer Kreise oder die Verwendung einer erweiterten Form des Mohrschen Kreises.

Zusammenfassung

Der Mohrsche Spannungskreis ist ein unverzichtbares Werkzeug in der Mechanik und Materialwissenschaft zur Visualisierung und Analyse von Spannungszuständen in Materialien.

Durch die Konstruktion dieses Kreises können Ingenieure und Wissenschaftler wichtige Informationen über die Hauptspannungen, maximale Schubspannungen und die Orientierung der Hauptschnittebenen gewinnen.

Diese Methode ist entscheidend für die Festigkeitsanalyse und das Design von Strukturen und Materialien, wodurch sie in vielen technischen und wissenschaftlichen Disziplinen weit verbreitet ist.

Was kommt als Nächstes?

Du hast nun alle relevanten Spannungen aus dem Mohrschen Spannungskreis abgelesen. Im nächsten Kursabschnitt schauen wir uns an, wie die Hauptrichtungen der Hauptnormalspannungen und Hauptschubspannungen abgelesen werden.

Was gibt es noch bei uns?

Optimaler Lernerfolg durch tausende Übungsaufgaben

Übungsbereich (Demo) - Lerne mit mehr als 4000 Übungsaufgaben für deine Prüfungen — Übungsbereich (Demo) – Lerne mit mehr als 4000 Übungsaufgaben für deine Prüfungen

Quizfrage 1

Quizfrage 2

“Wusstest du, dass unter jedem Kursabschnitt eine Vielzahl von verschiedenen interaktiven Übungsaufgaben bereitsteht, mit denen du deinen aktuellen Wissensstand überprüfen kannst?”

Alle Technikerschulen im Überblick

Zum Verzeichnis der Technikerschulen (Alles Rund um die Schulen) — Zum Verzeichnis der Technikerschulen

Kennst du eigentlich schon unser großes Technikerschulen-Verzeichnis für alle Bundesländer mit allen wichtigen Informationen (Studiengänge, Kosten, Anschrift, Routenplaner, Social-Media) ? Nein? – Dann schau einfach mal hinein:

Was ist Technikermathe?

Unser Dozent Jan erklärt es dir in nur 2 Minuten!

Oder direkt den > kostenlosen Probekurs < durchstöbern? – Hier findest du Auszüge aus jedem unserer Kurse!

Geballtes Wissen in derzeit 26 Kursen

Hat dir dieses Thema gefallen? – Ja? – Dann schaue dir auch gleich die anderen Themen zu den Kursen

WT3 (Werkstoffprüfung) und
TM1 (Technische Mechanik – Statik) an.

Lerne nun erfolgreich mit unserem Onlinekurs Technische Mechanik 1 — TM1 (Technische Mechanik)

Lerne nun erfolgreich mit unserem Onlinekurs Werkstofftechnik 3 — WT3 (Werkstoffprüfung)

Perfekte Prüfungsvorbereitung für nur 14,90 EUR/Jahr pro Kurs

++ Günstiger geht’s nicht!! ++

Oder direkt Mitglied werden und Zugriff auf alle 26 Kurse (inkl. Webinare + Unterlagen) sichern ab 7,40 EUR/Monat ++ Besser geht’s nicht!! ++