PH3 | Senkrechter Wurf nach oben [Grundlagen, Video, Beispiele, Aufgaben]

In dieser Lerneinheit behandeln wir das Thema: Senkrechter Wurf nach oben.

Für ein optimales Verständnis helfen dir 2 Videoclips und 4 ausführliche Aufgaben mit Zahlenwerten zu dem Thema.

Mehr zu diesem Thema und der Kinematik findest du im Kurs: PH3 – Einführung in die Kinematik.

Auch interessant! Alles zu Linearen Gleichungssystemen findest du im Kurs: Ma2-Lineare Gleichungssysteme

Senkrechter Wurf nach oben – Definition

Der senkrechte Wurf nach oben ist ein klassisches physikalisches Experiment, das die grundlegenden Prinzipien der Mechanik veranschaulicht.

Was ist der senkrechte Wurf nach oben?

Der senkrechte Wurf nach oben beschreibt die Bewegung eines Körpers, der mit einer Anfangsgeschwindigkeit vertikal nach oben geworfen wird. Während der Bewegung wirkt die Schwerkraft (Erdbeschleunigung $g$ ) ständig auf den Körper und verlangsamt ihn, bis er seine maximale Höhe erreicht. Danach fällt der Körper wieder zurück zur Erde.

Definition

Beim senkrechten Wurf nach oben wird ein Körper mit einer Anfangsgeschwindigkeit $v_0$ senkrecht nach oben geworfen. Die Bewegung wird durch die Erdbeschleunigung $g$ beeinflusst, die den Körper nach unten zieht.

Bei dem senkrechten Wurf nach oben handelt es sich um die gradlinige Bewegung eines Körpers in vertikale Richtung, also in Richtung der Höhenkoordinate. Der senkrechte Wurf nach oben wird in eine Aufwärtsbewegung und eine Abwärtsbewegung unterteilt.

Senkrechter Wurf nach oben, Beispiel, Formel, Definition, Video, Wurf nach oben

Beim senkrechten Wurf nach oben unterscheiden wir zwischen der Aufwärtsbewegung und der Abwärtsbewegung.

Senkrechter Wurf nach oben, Wurf nach oben, Beispiel, Aufwärtsbewegung, Abwärtsbewegung, freier Fall — Senkrechter Wurf nach oben: Aufwärtsbewegung, Abwärtsbewegung

Senkrechter Wurf nach oben – Beispiele im Alltag

Nun folgen einige Beispiele für einen senkrechten Wurf nach oben im Alltag:

Ein Ball, der senkrecht nach oben geworfen wird und dann wieder herunterfällt.
Ein Springbrunnen, bei dem das Wasser senkrecht nach oben spritzt und dann wieder nach unten fällt.
Das Hochwerfen einer Münze in die Luft, bei dem sie senkrecht nach oben fliegt und dann zurückfällt.
Das Werfen eines Frisbees oder eines Flugzeugs nach oben, wobei es eine gewisse Höhe erreicht und dann wieder zu Boden fällt.
Das Hochstoßen einer Spielzeugrakete in die Luft, bei dem sie senkrecht nach oben steigt und dann wieder herunterkommt.

Diese Beispiele zeigen Situationen im Alltag, bei denen ein Objekt senkrecht nach oben geworfen wird und dann aufgrund der Schwerkraft wieder zur Erdoberfläche fällt.

Senkrechter Wurf nach oben – Ausnahmen

Ein senkrechter Wurf nach oben folgt normalerweise den Gesetzen der Physik.

Es gibt jedoch einige Ausnahmen oder spezielle Fälle, in denen ein senkrechter Wurf nach oben nicht vollständig vorliegt. Hier sind einige solcher Ausnahmen:

Luftwiderstand: Bei Objekten mit großer Oberfläche oder hoher Geschwindigkeit kann der Luftwiderstand eine Rolle spielen und die Bewegung beeinflussen. Der Luftwiderstand kann dazu führen, dass das Objekt langsamer fällt oder eine nicht ganz symmetrische Flugbahn hat.
Externe Kräfte: In einigen Fällen können externe Kräfte auf das Objekt einwirken und seine Bewegung beeinflussen. Beispielsweise kann bei einem senkrechten Wurf nach oben in der Nähe von starken Magnetfeldern oder elektrischen Feldern die Bewegung des Objekts durch diese Kräfte beeinflusst werden.
Elastische Rückstoßkraft: Bei bestimmten Objekten, die spezielle Eigenschaften haben, kann es vorkommen, dass das Objekt nach dem senkrechten Wurf nach oben nicht genau auf den Ausgangspunkt zurückfällt. Ein Beispiel dafür ist ein elastisches Objekt wie ein Gummiball oder eine Feder, bei dem eine Rückstoßkraft wirkt und das Objekt beim Fall eine andere Bahn oder Höhe erreichen lässt.

Es ist wichtig zu beachten, dass diese Ausnahmen spezielle Fälle darstellen, in denen bestimmte Kräfte oder Bedingungen die Bewegung eines senkrechten Wurfs nach oben beeinflussen können. In den meisten alltäglichen Situationen folgt ein Objekt, das senkrecht nach oben geworfen wird, jedoch den Gesetzen der Schwerkraft und fällt aufgrund der Gravitationskraft zurück zur Erdoberfläche.

Aufwärtsbewegung – Formeln

Beim senkrechten Wurf nach oben wird ein Körper mit einer bestimmten Anfangsgeschwindigkeit $v_0$ senkrecht nach oben geworfen. Hierbei ist $h_0$ die Abwurfhöhe, also die Höhe, von welcher aus der Körper nach oben geworfen wird. $h_s$ ist die Steighöhe, also diejenige Höhe, die der Körper nach dem Abwurf nach oben seigt. Die Abwurfhöhe $h_0$ ist nicht unbedingt mit der Aufprallhöhe (nachdem der Ball wieder zu Boden fällt) identisch.

Nach dem Abwurf ausgehend von der Höhe $h_0$ , befindet sich der Körper in der Luft und es wirkt die Fallbeschleunigung $g$ auf ihn, welche dazu führt, dass seine Bewegung verlangsamt wird. Der Ball steigt insgesamt $h_0$ nach oben, solange, bis die Geschwindigkeit Null ist. Ist der der Fall, so hat der Körper seine maximale Höhe $H$ erreicht und die Aufwärtsbewegung endet.

Senkrechter Wurf nach oben | Formel

$v = 0 \rightarrow H$

Am höchsten Punkt $H$ , ist die Geschwindigkeit gleich Null. Genau an dieser Stelle ändert der Körper seine Bewegung von einer Aufwärtsbewegung in eine Abwärtsbewegung.

Für die Aufwärtsbewegung gelten die folgenden Formeln:

$v = v_0 - g \cdot t$	Geschwindigkeit
$s = v_0 \cdot t - \dfrac{1}{2} \cdot g \cdot t^2$	zurückgelegter Weg (nach oben)
$v = +\sqrt{v_0^2 - 2 \cdot g \cdot (s - h_0)}$	Geschwindigkeit
$t_s = \dfrac{v_0}{g}$	Steigzeit
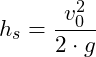$h_s = \dfrac{v_0^2}{2 \cdot g}$	Steighöhe
$H = h_0 + h_s$	Gesamthöhe

Bei der obigen Gleichung zur Berechnung des Weges $s$ zeigt der 1. Term den Wurf mit der Anfangsgeschwindigkeit $v_0$ nach oben auf, der zweite Term zeigt die auf den Körper wirkende Fallbeschleunigung $g$ an, welche den Körper nach unten zieht.

Abwärtsbewegung (freier Fall) – Formeln

Vom höchsten Punkt $H$ ausgehend, fällt der Körper im freien Fall zur Erde (siehe: Freier Fall). Auf den Körper wirkt dabei die Fallbeschleunigung $g = 9,81 m/s^2$ . Unmittelbar beim Aufprall erreicht der Körper seine höchste Fallgeschwindigkeit $v_{max}$ .

Wie schon oben angemerkt, müssen Aufprallhöhe und Abwurfhöhe nicht zusammenfallen. Wenn du einen Ball im Stand nach oben wirfst und dieser danach auf den Boden aufprallt, so ist die Höhe des Abwurfs (ungefähr deine Kopfhöhe) und die Höhe des Aufpralls (der Boden) nicht identisch.

Für die Abwärtsbewegung gelten die Formeln des freien Falls:

$v = g \cdot t$	Geschwindigkeit in Abhängigkeit von der Zeit
$s = \dfrac{1}{2} \cdot g \cdot t^2$	zurückgelegter Weg
$h = H - \dfrac{1}{2} \cdot g \cdot t^2$	Höhe
$v = \sqrt{2 \cdot g \cdot s}$	Geschwindigkeit in Abhängigkeit vom zurückgelegten Weg
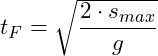$t_F = \sqrt{\dfrac{2 \cdot s_{max}}{g}}$	Fallzeit
$t_F = \dfrac{v_{max}}{g}$	Fallzeit

Video – Senkrechter Wurf nach oben

Im nachfolgenden Video zeige ich dir, wie du die obigen Gleichungen anwendest.

Betrachten wir zum besseren Verständnis der Gleichungen das nachfolgende Beispiel.

Senkrechten Wurf nach oben Beispiel

Aufgabenstellung

Eine Stahlkugel mit einer Masse von $m = 2 kg$ wird mit einer Anfangsgeschwindigkeit von $v_0 = 15 m/s$ senkrecht nach oben geworfen. Der Luftwiderstand soll vernachlässigt werden.

a) Wie hoch ist die maximale Steighöhe und die Steigzeit?

b) Mit welcher Geschwindigkeit trifft die Kugel auf dem Boden auf, wenn sie in 2,4m Höhe abgeworfen wurde?

c) Wie lang ist die gesamte Flugzeit?

Gegeben:

$v_0 = 15 m/s$

$g = 9,81 m/s^2$

Masse ist unerheblich, da Luftwiderstand vernachlässigt wird.

Lösung

Lösung a) Maximale Steighöhe, Steigzeit

Wir berechnen zunächst, aus den gegebenen Werte, die Steighöhe und die Steigzeit (siehe Aufwärtsbewegung):

Steigzeit: $t_s = \dfrac{v_0}{g}$

Steighöhe: 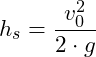$h_{s} = \dfrac{v_0^2}{2 \cdot g}$

Einsetzen der gegebenen Werte:

$t_s = \dfrac{15 m/s}{9,81 m/s^2} = 1,53 s$

$h_s = \dfrac{(15 m/s)^2}{2 \cdot 9,81 m/s^2} = 11,47 m$

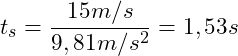
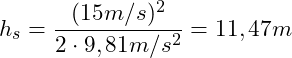
Die Kugel erreicht nach 1,53s ihre maximale Steighöhe von 11,47 m. Die Steighöhe ist hierbei nicht gleich der maximalen Höhe $H$ über dem Boden, da die Kugel von einer gewissen Höhe $h_0$ abgeworfen wird (nicht vom Boden aus). Die tatsächliche Höhe der Kugel kann man berechnen aus:

Gesamthöhe: $H = h_0 + h_s$

Zur Berechnung der maximalen Höhe $H$ müssen Steighöhe $h_s$ und Abwurfhöhe $h_0$ bekannt sein.

Lösung b) Geschwindigkeit

In dieser Aufgabenstellung ist nun die Abwurfhöhe $h_0 = 2,4m$ gegeben. Wir können hieraus die maximale Flughöhe (vom Boden ausgehend) bestimmen:

$H = h_0 + h_s = 2,4m + 11,47 m = 13,87 m$

Die Kugel wird abgeworfen bei einer Höhe von 2,4m, steigt dann nochmal 11,47 m hoch und erreicht damit eine Höhe von 13,87m. Danach fällt die Kugel zu Boden. Hier gelten die Gleichungen des freien Falls. In dieser Aufgabenstellung b) soll nun die Geschwindigkeit bestimmt werden, mit welcher die Kugel auf den Boden auftrifft:

Dazu ziehen wir die folgende Formel heran:

$v = \sqrt{2 \cdot g \cdot s}$

Hierbei ist $s$ nichts anderes als der Weg der Kugel vom höchsten Punkt $H$ bis zum Boden, also die berechneten 13,87 m. Das ist die Höhe, bei welcher die Kugel wieder nach unten fällt:

$v = \sqrt{2 \cdot 9,81 m/s^2 \cdot 13,87m} = 16,5 m/s$

Die Kugel weist unmittelbar beim Aufprall auf den Boden eine Geschwindigkeit von 16,5 m/s auf.

Lösung c) Flugzeit

Wir suchen in diesem Aufgabenteil die gesamte Zeit, welche die Kugel vom Abwurf bis zum Aufprall auf den Boden benötigt. Die Steigzeit haben wir bereits in a) berechnet. Diese beträgt:

$t_s = 1,53 s$

Wir benötigen noch die Zeit, welche die Kugel sich im freien Fall befindet. Diese berechnen wir mittels der folgenden Gleichungen:

$t_F = \sqrt{\dfrac{2 s_{max}}{g}}$

$t_F = \dfrac{v_{max}}{g}$

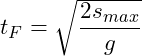
Eine der beiden Gleichungen kann herangezogen werden, um die Fallzeit zu berechnen. Die Kugel fällt insgesamt im freien Fall $s_{max} = 13,87 m$ bis sie den Boden erreicht:

$t_F = \sqrt{\dfrac{2 \cdot 13,87 m}{9,81 m/s^2}} = 1,68 s$

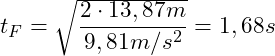
Alternativ berechnen wir die Fallzeit über die maximale Geschwindigkeit $v_{max} = 16,5 m/s$ unmittelbar beim Aufprall auf den Boden:

$t_F = \dfrac{16,5 m/s}{9,81 m/s^2} = 1,68s$

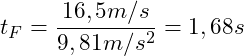
Als nächstes addieren wir die Steigzeit und Fallzeit, um die gesamte Flugzeit zu bestimmen:

$t = t_s + t_F = 1,53s + 1,68s = 3,21s$

Die gesamte Flugdauer der Kugel beträgt 3,21 Sekunden vom Abwurf bis zum Aufprall auf den Boden.

Anwendung des senkrechten Wurfes nach oben

Physikunterricht: Der senkrechte Wurf nach oben wird häufig als Beispiel verwendet, um die Prinzipien der Kinematik und Dynamik zu erklären.
Sport: Beim Hochsprung oder Werfen eines Balls sind die Prinzipien des senkrechten Wurfs nach oben relevant.
Technik: In der Technik und Ingenieurwissenschaften hilft das Verständnis des senkrechten Wurfs, Bewegungen von Projektilen und anderen Objekten zu analysieren.

Mögliche Fragestellungen | Häufig gestellte Fragen (FAQs)

1. Was ist der senkrechte Wurf nach oben?

Der senkrechte Wurf nach oben beschreibt die Bewegung eines Körpers, der mit einer Anfangsgeschwindigkeit vertikal nach oben geworfen wird und unter der Wirkung der Schwerkraft wieder zurückfällt.

2. Welche Kräfte wirken beim senkrechten Wurf nach oben?

Hauptsächlich wirkt die Erdbeschleunigung (g) auf den Körper, die ihn nach unten zieht.

3. Wie berechnet man die maximale Höhe?

Die maximale Höhe wird mit der Formel $h_{max} = \frac{v_0^2}{2g}$ berechnet.

4. Wie berechnet man die Gesamtdauer des Flugs?

Die Gesamtdauer des Flugs ist $t_{gesamt} = \frac{2 \cdot v_0}{g}$

5. Wo wird der senkrechte Wurf nach oben angewendet?

Der senkrechte Wurf nach oben wird in Physik, Sport und Technik angewendet, um Bewegungen von Objekten zu analysieren.

Zusammenfassung

Der senkrechte Wurf nach oben ist eine klassische Bewegung unter dem Einfluss der Schwerkraft. Mit einer Anfangsgeschwindigkeit nach oben geworfen, erreicht der Körper eine maximale Höhe und fällt dann wieder zurück.

Die Bewegung lässt sich durch die Anfangsgeschwindigkeit und die Erdbeschleunigung beschreiben, und die Berechnungen umfassen die maximale Höhe, die Zeit zum Erreichen dieser Höhe und die Gesamtdauer des Flugs.

Dieses Konzept ist sowohl theoretisch interessant als auch praktisch anwendbar in verschiedenen Bereichen wie Physik, Sport und Technik.

Was kommt als Nächstes?

Nachdem du jetzt das Prinzip zum Thema Senkrechter Wurf nach oben kennst, schauen wir uns im nachfolgenden Kurstext weitere Beispiele zum senkrechten Wurf nach oben an!

Was gibt es noch bei uns?

Optimaler Lernerfolg durch tausende Übungsaufgaben

Übungsbereich (Demo) - Lerne mit mehr als 4000 Übungsaufgaben für deine Prüfungen — Übungsbereich (Demo) – Lerne mit mehr als 4000 Übungsaufgaben für deine Prüfungen

Quizfrage 1

Quizfrage 2

“Wusstest du, dass unter jedem Kursabschnitt eine Vielzahl von verschiedenen interaktiven Übungsaufgaben bereitsteht, mit denen du deinen aktuellen Wissensstand überprüfen kannst?”

Alle Technikerschulen im Überblick

Zum Verzeichnis der Technikerschulen (Alles Rund um die Schulen) — Zum Verzeichnis der Technikerschulen

Kennst du eigentlich schon unser großes Technikerschulen-Verzeichnis für alle Bundesländer mit allen wichtigen Informationen (Studiengänge, Kosten, Anschrift, Routenplaner, Social-Media) ? Nein? – Dann schau einfach mal hinein:

Was ist Technikermathe?

Unser Dozent Jan erklärt es dir in nur 2 Minuten!

Oder direkt den > kostenlosen Probekurs < durchstöbern? – Hier findest du Auszüge aus jedem unserer Kurse!

Geballtes Wissen in derzeit 26 Kursen

Hat dir dieses Thema gefallen? – Ja? – Dann schaue dir auch gleich die anderen Themen zu den Kursen

WT3 (Werkstoffprüfung) und
TM1 (Technische Mechanik – Statik) an.

Lerne nun erfolgreich mit unserem Onlinekurs Technische Mechanik 1 — TM1 (Technische Mechanik)

Lerne nun erfolgreich mit unserem Onlinekurs Werkstofftechnik 3 — WT3 (Werkstoffprüfung)

Perfekte Prüfungsvorbereitung für nur 14,90 EUR/Jahr pro Kurs

++ Günstiger geht’s nicht!! ++

Oder direkt Mitglied werden und Zugriff auf alle 26 Kurse (inkl. Webinare + Unterlagen) sichern ab 7,40 EUR/Monat ++ Besser geht’s nicht!! ++