MA3 – Sattelpunkt einer ln-Funktion

Wir wollen uns als nächstes anschauen, wie der Sattelpunkte einer ln-Funktion bestimmt wird. In dieser Lerneinheit schauen wir uns an, was ein Sattelpunkt ist und zeigen wie der Sattelpunkt einer ln-Funktion berechnet wird:

Für ein optimales Verständnis helfen dir drei ausführliche Beispiele mit Zahlenwerten zu dem Thema.

Mehr zu diesem Thema und der Mathematik findest du im Kurs: Onlinekurs MA3 – Kurvendiskussion.

Oder lieber mit den Grundlagen starten? Alles dazu findest du im Kurs: Ma1-Grundlagen der Mathematik

Sattelpunkt einer ln-Funktion | Grundlagen

Was ist der Sattelpunkt einer ln-Funktion?

Ein Sattelpunkt ist ein spezieller Punkt auf dem Graphen einer Funktion, bei dem die erste Ableitung null ist, die Funktion jedoch keine Extremstelle hat. Das Finden eines Sattelpunktes bei einer natürlichen Logarithmusfunktion $(ln)$ ist besonders interessant und erfordert präzise Analyse der Ableitungen.

Grundprinzipien

Definition eines Sattelpunktes:
- Ein Sattelpunkt ist ein Punkt $(x, f(x))$ , bei dem die erste Ableitung $f'(x) = 0$ und die zweite Ableitung $f''(x) = 0$ ist. Der Funktionswert an diesem Punkt ist weder ein Maximum noch ein Minimum.
Natürliche Logarithmusfunktion:
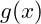- Die allgemeine Form einer natürlichen Logarithmusfunktion ist $f(x) = ln(g(x))$ , wobei $g(x)$ eine differenzierbare Funktion ist.

Eine Funktion hat einen Sattelpunkt (auch: Terrassenpunkt), wenn sie an einer Stelle gleichzeitig einen Wendepunkt und eine waagerechte Tangente besitzt. Das heißt, dass sowohl die 1. Ableitung als auch die 2. Ableitung zu Null werden.

ln-Funktion mit Sattelpunkt, Punkt ohne Steigung, Wendepunkt | Kurvendiskussion

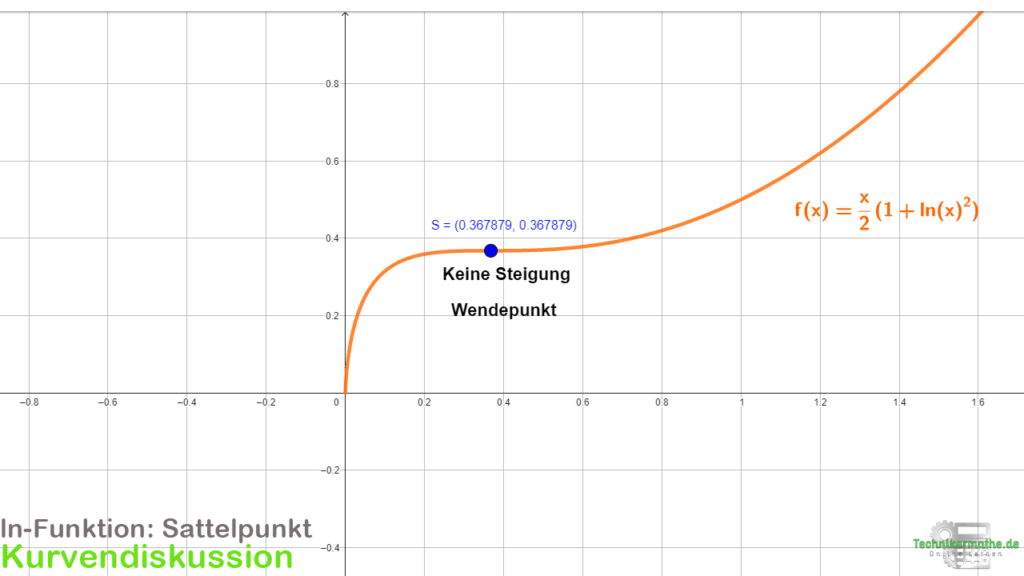
Bei einem Sattelpunkt liegt also ein Wendepunkt vor, d.h. die Funktion wechselt von einer Linkskrümmung in eine Rechtskrümmung oder umgekehrt. Zusätzlich haben wir in diesem Punkt keine Steigung gegeben, weil auch die erste Ableitung gleich Null ist. Für die obige Funktion wollen wir den angezeigten Sattelpunkt rechnerisch ermitteln.

Auszug aus unserem Onlinekurs MA3 – Kurvendiskussion.

Sattelpunkte allgemein

Zur Bestimmung der Sattelpunkte von Funktionen benötigen wir die 1. Ableitung, die 2. Ableitung und die 3. Ableitung der Funktion. Schauen wir uns mal an, wie die Sattelpunkte allgemein bestimmt werden.

Sattelpunkte bestimmen

Bilde die 1. Ableitung der Funktion und setze diese gleich Null: f'(x) = 0
Löse die 1. Ableitung nach x auf.
Bilde die 2. Ableitung der Funktion. Setze den aus 2. ermittelten x-Wert in die 2. Ableitung ein.
Die 2. Ableitung muss Null ergeben: f”(x) = 0
Bilde die 3. Ableitung. Ist die dritte Ableitung ungleich Null, dann ist ein Sattelpunkt gegeben: f”'(x) ≠ 0
Ist die 3. Ableitung von x abhängig, so setze den aus 2. ermittelten x-Wert in die 3. Ableitung ein.
Setze den ermittelten x-Wert aus 2. in die Ausgangsfunktion f(x) ein, um den dazugehörigen y-Wert zu bestimmen.

Vorgehensweise: Sattelpunkte einer ln-Funktion

Gegeben sei die folgende verschachtelte e-Funktion:

$f(x) = \frac{x}{2} \cdot (1 + ln(x)^2)$

Untersuche die Funktion auf Sattelpunkte!

Erste Ableitung bilden

Wir bilden die 1.Ableitung, indem wir die Produktregel anwenden:

$f(x) = u(x) \cdot v(x)$

$f'(x) = u'(x) \cdot v(x) + v'(x) \cdot u(x)$

Für unsere Funktion gilt:

$u(x) = \frac{x}{2}$

$v(x) = 1+ln(x)^2$

Ableiten:

$u'(x) = \frac{1}{2}$

$v'(x)$ Kettenregel auf ln anwenden, Konstante 1 fällt weg

Wir müssen für die ln(x)² Funktion die Kettenregel anwenden. Wir haben hier einen Exponenten an der ln-Funktion gegeben (nicht am Klammerausdruck). Das bedeutet, dass wir hier den Exponenten als äußere Ableitung berücksichtigen.

Wir haben die folgende äußere und innere Ableitung gegeben:

$(ln(x)^2)' = 2 \cdot ln(x)$ äußere Ableitung

$ln(x)'$ Innere Ableitung

Die innere Ableitung ist zudem noch in eine innere und äußere Ableitung zu unterteilen. Die innere Ableitung ist die Ableitung des Ausdrucks in der Klammer:

$x' = 1$

Die äußere Ableitung ist die Ableitung des Logarithmus:

$ln(x)' = \frac{1}{x}$

Die Ableitung des Logarithmus ln(x) ergibt also:

$1 \cdot \frac{1}{x} = \frac{1}{x}$ Innere Ableitung

Innere mal äußere Ableitung ergibt dann:

$v'(x) = 2 \cdot ln(x) \cdot \frac{1}{x}$

Wir wenden die Produktregel an:

$f'(x) = u'(x) \cdot v(x) + v'(x) \cdot u(x)$

$f'(x) = \frac{1}{2} \cdot (1+ln(x)^2) + 2 \cdot ln(x) \cdot \frac{1}{x} \cdot \frac{x}{2}$

$f'(x) = \frac{1}{2} \cdot (1+ln(x)^2) + ln(x)$

$f'(x) = \frac{1}{2}ln(x)^2 + ln(x) + \frac{1}{2}$

Wir können hier die 1.binomische Formel anwenden und den Faktor 1/2 davor schreiben:

$f'(x) = \frac{1}{2}(ln(x) + 1)^2$ 1.Ableitung

Erste Ableitung nach x auflösen

Im nächsten Schritt setzen wir die 1. Ableitungen gleich Null und lösen nach x auf:

$f'(x) = \frac{1}{2}(ln(x) + 1)^2 = 0$

Die obige Funktion stellen wir nach x um:

$\frac{1}{2}(ln(x) + 1)^2 = 0$ |*2

$(ln(x) + 1)^2 = 0$ |Wurzel

$ln(x) + 1 = 0$ |-1

$ln(x) = -1$ |e-Funktion

$x= e^{-1}$ Nullstelle der 1.Ableitung

Zweite Ableitung bilden und x-Wert einsetzen

Wir bilden als nächstes die 2.Ableitung und setzen die ermittelten x-Werte der ersten Ableitung in die zweite Ableitung ein. Wird diese dann zu Null, so liegt möglicherweise ein Sattelpunkt vor.

Die 2. Ableitung wird aus der 1. Ableitung gebildet:

$f'(x) = \frac{1}{2}(ln(x) + 1)^2$ 1.Ableitung

Wir müssen hier die innere und äußere Ableitung betrachten. Die äußere Ableitung ist der Exponent an der Klammer. Die innere Ableitung ist die ln-Funktion, welche ebenfalls in eine innere und äußere Ableitung unterteilt werden muss.

Äußere Ableitung

$v(x) = \frac{1}{2}(ln(x) + 1)^2$

$v'(x) = 2 \cdot \frac{1}{2}(ln(x) + 1) = (ln(x) + 1)$

Innere Ableitung

$u(x) = ln(x) + 1$

$u'(x)$

Konstante 1 fällt weg. Wir betrachten also noch die ln-Funktion. Einmal den Klammerausdruck ableiten:

$x' = 1$

Dann die ln-Funktion ableiten:

$ln(x)' = \frac{1}{x}$

Beide inneren Ableitungen miteinander multiplizieren:

$u'(x) = 1 \cdot \frac{1}{x} = \frac{1}{x}$

Jetzt können wir die Kettenregel für die äußere und innere Ableitung anwenden:

$f''(x) = v'(x) \cdot u'(x) = (ln(x) + 1) \cdot \frac{1}{x}$ 2.Ableitung

Einsetzen des berechneten x-Werts aus der 1.Ableitung:

$f''(x= e^{-1}) = (ln(e^{-1}) + 1) \cdot \frac{1}{e^{-1}} = 0$

Bei x = e^-1 liegt möglicherweise ein Sattelpunkt vor, da die 2. Ableitung nach Einsetzen des x-Wertes aus der 1.Ableitung zu Null wird.

Dritte Ableitung bilden

Die 3. Ableitung wird bestimmt, indem die 2.Ableitung abgleitet wird:

$f''(x) = (ln(x) + 1) \cdot \frac{1}{x}$ 2.Ableitung

Wir bilden die 3.Ableitung, indem wir die Produktregel anwenden:

$f''(x) = u(x) \cdot v(x)$

$f'''(x) = u'(x) \cdot v(x) + v'(x) \cdot u(x)$

Für unsere Funktion gilt:

$u(x) = ln(x) + 1$

$v(x) = \frac{1}{x} = x^{-1}$

Ableiten:

$u'(x)$

Die Konstante 1 fällt weg. Für ln(x) müssen wir den Klammerausdruck und den Logarithmus ableiten und beide Ableitungen miteinander multiplizieren:

$x'=1$

$ln(x)'=\frac{1}{x}$

$u'(x) = 1 \cdot \frac{1}{x} = \frac{1}{x}$

$v'(x) = -x^{-2} = -\frac{1}{x^2}$

Jetzt wenden wir die Produktregel an:

$f'''(x) = \frac{1}{x} \cdot \frac{1}{x} + -\frac{1}{x^2} \cdot (ln(x) + 1)$

$f'''(x) = \frac{1}{x^2} - \frac{1}{x^2} \cdot (ln(x) + 1)$

$f'''(x) = -\frac{1}{x^2} (-1 + ln(x) + 1)$

$f'''(x) = \frac{1}{x^2} ln(x)$

Die dritte Ableitung ist von x abhängig. Wir wissen, dass bei x = e^-1 womöglich ein Sattelpunkt vorliegt. Wir können das nun anhand der dritten Ableitung prüfen, indem wir x = e^-1 in die dritte Ableitung einsetzen:

$f'''(x = e^{-1}) = \frac{1}{(e^{-1})^2} ln(e^{-1}) = -7,39 \neq 0$

Da die dritte Ableitung ungleich Null ist, handelt es sich hierbei um einen Wendepunkt der Funktion. Die Funktion wechselt an dieser Stelle (f”'(x) <0) von einer Rechtskrümmung in eine Linkskrümmung.

Merk’s dir!

Wir haben bei x = e^-1 einen Sattelpunkt gegeben, da in diesem Punkt keine Steigung der Funktion vorliegt und zusätzlich ein Wendepunkt gegeben ist.

Sattelpunkt einer ln-Funktion bestimmen

Damit wir den Sattelpunkt angeben können, benötigen wir noch den zum x-Wert dazugehörigen y-Wert. Dazu setzen wir den x-Wert in die Ausgangsfunktion ein:

$f(x = e^{-1})= \frac{e^{-1}}{2} \cdot (1+ln(e^{-1}))^2 = 0,368..= e^{-1}$

Der Sattelpunkt ist also gegeben bei:

S(e^-1|e^-1)

In der folgenden Grafik siehst du den Sattelpunkt der ln-Funktion eingezeichnet:

Sattelpunkt einer ln-Funktion, MA3, ln-Funktion, Sattelpunkt, Logarithmusfunktion, Beispiel

In der obigen Grafik siehst du im Punkt S(e^-1|e^-1) bzw. gerundet S(0,368|0,368) den Sattelpunkt der Funktion. Ein Sattelpunkt ist dann gegeben, wenn die Funktion in diesem Punkt keine Steigung aufweist (f'(x) = 0) und wenn zusätzlich ein Wendepunkt (f”'(x) ≠ 0) gegeben ist, die Funktion also ihr Krümmungsverhalten wechselt. Vor dem Sattelpunkt weist die Funktion eine Rechtskrümmung auf, nach dem Sattelpunkt eine Linkskrümmung.

Anwendung der Sattelpunktanalyse

Mathematik: Untersuchung von Kurvenverläufen und Funktionsverhalten.
Wirtschaft: Analyse von Gewinn- und Kostenfunktionen.
Naturwissenschaften: Untersuchung von Wachstumsprozessen und Halbwertszeiten.

Mögliche Fragestellungen | Häufig gestellte Fragen (FAQs)

1. Was ist ein Sattelpunkt?

Ein Sattelpunkt ist ein Punkt auf dem Graphen einer Funktion, bei dem die erste Ableitung null ist, die Funktion jedoch keine Extremstelle hat.

2. Wie findet man einen Sattelpunkt bei einer ln-Funktion?

Durch Berechnung der ersten und zweiten Ableitung und Überprüfung der Bedingungen $f'(x) = 0$ und $f''(x) \neq 0$ .

3. Was ist die natürliche ln-Funktion?

Die natürliche Logarithmusfunktion ist $ln(x)$ , die Umkehrfunktion der Exponentialfunktion $e^x$ .

4. Warum sind Sattelpunkte wichtig?

Sie geben Einblick in das Monotonieverhalten und die Struktur des Graphen einer Funktion.

5. Gibt es immer einen Sattelpunkt bei ln-Funktionen?

Nein, Sattelpunkte existieren nur, wenn die spezifischen Bedingungen erfüllt sind.

Zusammenfassung

Die Bestimmung von Sattelpunkten bei natürlichen Logarithmusfunktionen erfordert die Berechnung der ersten und zweiten Ableitungen und die Überprüfung der notwendigen Bedingungen.

Diese Methode ist in vielen Bereichen wie Mathematik, Wirtschaft und Naturwissenschaften von großer Bedeutung und hilft, das Verhalten und die Struktur von Funktionen präzise zu verstehen.

Was kommt als Nächstes?

In der folgenden Lerneinheit zeigen wir dir, wie Ableiten mit der Produktregel abläuft.

Was gibt es noch bei uns?

Optimaler Lernerfolg durch tausende Übungsaufgaben

Übungsbereich (Demo) - Lerne mit mehr als 4000 Übungsaufgaben für deine Prüfungen — Übungsbereich (Demo) – Lerne mit mehr als 4000 Übungsaufgaben für deine Prüfungen

Quizfrage 1

Quizfrage 2

“Wusstest du, dass unter jedem Kursabschnitt eine Vielzahl von verschiedenen interaktiven Übungsaufgaben bereitsteht, mit denen du deinen aktuellen Wissensstand überprüfen kannst?”

Alle Technikerschulen im Überblick

Zum Verzeichnis der Technikerschulen (Alles Rund um die Schulen) — Zum Verzeichnis der Technikerschulen

Kennst du eigentlich schon unser großes Technikerschulen-Verzeichnis für alle Bundesländer mit allen wichtigen Informationen (Studiengänge, Kosten, Anschrift, Routenplaner, Social-Media) ? Nein? – Dann schau einfach mal hinein:

Was ist Technikermathe?

Unser Dozent Jan erklärt es dir in nur 2 Minuten!

Oder direkt den > kostenlosen Probekurs < durchstöbern? – Hier findest du Auszüge aus jedem unserer Kurse!

Geballtes Wissen in derzeit 26 Kursen

Hat dir dieses Thema gefallen? – Ja? – Dann schaue dir auch gleich die anderen Themen zu den Kursen

WT3 (Werkstoffprüfung) und
TM1 (Technische Mechanik – Statik) an.

Lerne nun erfolgreich mit unserem Onlinekurs Technische Mechanik 1 — TM1 (Technische Mechanik)

Lerne nun erfolgreich mit unserem Onlinekurs Werkstofftechnik 3 — WT3 (Werkstoffprüfung)

Perfekte Prüfungsvorbereitung für nur 14,90 EUR/Jahr pro Kurs

++ Günstiger geht’s nicht!! ++

Oder direkt Mitglied werden und Zugriff auf alle 26 Kurse (inkl. Webinare + Unterlagen) sichern ab 7,40 EUR/Monat ++ Besser geht’s nicht!! ++