MA3 – Punktsymmetrie bei e-Funktionen

In dieser Lerneinheit wollen wir uns anschauen, was die Punktsymmetrie bei e-Funktionen ist und wie diese bestimmt wird.

Für ein optimales Verständnis helfen dir drei ausführliche Beispiele mit Zahlenwerten zu dem Thema.

Mehr zu diesem Thema und der Mathematik findest du im Kurs: Onlinekurs MA3 – Kurvendiskussion.

Oder lieber mit den Grundlagen starten? Alles dazu findest du im Kurs: Ma1-Grundlagen der Mathematik

Punktsymmetrie | Grundlagen

Was ist Punktsymmetrie bei e-Funktionen?

Punktsymmetrie ist ein wichtiger Begriff in der Mathematik, der sich auf die Symmetrie einer Funktion bezieht. Eine Funktion ist punktsymmetrisch zu einem Punkt $P(a,b)$ , wenn für jeden Punkt $(x, f(x))$ auf dem Graphen der Punkt $(2a - x, 2b - f(x))$ ebenfalls auf dem Graphen liegt. Im Fall der e-Funktion $(f(x) = e^x)$ und verwandten Funktionen ist das Verständnis dieser Symmetrieeigenschaften von großer Bedeutung.

Grundprinzipien

Definition der Punktsymmetrie:
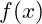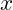- Eine Funktion $f(x)$ ist punktsymmetrisch zu einem Punkt $(a, b)$ , wenn $f(2a - x) = 2b - f(x)$ für alle $x$ in der Domäne der Funktion.
E-Funktionen:
- Die Basis-e-Exponentialfunktion $f(x) = e^x$ ist weder achsensymmetrisch noch punktsymmetrisch zur y-Achse oder zum Ursprung.
- Modifizierte e-Funktionen wie $f(x) = e^{-x}$ oder $f(x) = e^x - k$ können punktsymmetrisch sein, je nach Transformation und Verschiebung.

Punktsymmetrie allgemein

Eine Figur heißt punktsymmetrisch, wenn sie durch die Spiegelung an einem Punkt, dem sogenannten Symmetriepunkt, auf sich selbst abgebildet wird. Die Funktion wird dabei an dem Symmetriepunkt um 180° gedreht. Als Symmetriepunkt betrachten wir hier den Koordinatenursprung (0,0).

Eine Funktion ist zum Koordinatenursprung (0,0) punktsymmetrisch, wenn sie nur ungerade Exponenten aufweist. Die Funktion darf außerdem keine Konstante gegeben haben, da ansonsten keine Punktsymmetrie vorliegt.

Die Bedingung für die Punktsymmetrie lautet mathematisch:

Punktsymmetrie

$-f(x) = f(-x)$

Die gegebene Funktion multipliziert mit (-1) und die Funktion beim Einsetzen von x = -x müssen identisch sein.

Schauen wir uns dazu mal ein Beispiel an.

Beispiel 1: Punktsymmetrie bei e-Funktionen

Gegeben sei die folgende verschachtelte e-Funktion:

$f(x) = x^3 \cdot e^{4x^2}$

Ist die Funktion punktsymmetrisch in Bezug auf den Koordinatenursprung? Überprüfe!

Wir wollen die obige verschachtelte e-Funktion (Funktion mit e-Funktion, quadratischer Funktion im Exponenten und kubischer Funktion) auf Punktsymmetrie in Bezug auf den Koordinatenursprung überprüfen:

$-f(x) = f(-x)$ Punktsymmetrie

Wir betrachten zunächst die Ausgangsfunktion und setzen hier ein Minuszeichen vor die gesamte Funktion:

$-f(x) = - [x^3 \cdot e^{4x^2}]$

(1) $-f(x) = - x^3 \cdot e^{4x^2}$

Danach setzen wir in die Ausgangsfunktion für x = -x ein:

$f(-x) = (-x)^3 \cdot e^{4(-x)^2}$

Bei ungeraden Exponenten [wie z.B. (-x)³] bleibt das Minuszeichen stehen [-x³]. Bei gerade Exponenten fällt das Minuszeichen weg [(-x)² = x²]

Damit ergibt sich:

(2) $f(-x) = -x^3 \cdot e^{4x^2}$

Die Bedingung lautet nun, dass beide Funktionen (1) und (2) gleich sein müssen. In unserem Fall sind die beiden Funktionen gleich:

$-f(x) = f(-x)$

Damit liegt für die gegebene Funktion Punktsymmetrie im Koordinatenursprung vor:

Punktsymmetrie bei e-Funktionen, Punktsymmetrie, e-Funktionen, Exponentialfunktionen

Drehst du den linken Teil der Funktion um 180° um den Koordinatenursprung, dann erhältst du den rechten Teil der Funktion. Damit liegt hier Punktsymmetrie zum Koordinatenursprung vor.

Beispiel 2: Punktsymmetrie bei e-Funktionen

Gegeben sei die folgende verschachtelte e-Funktion:

$f(x) = (x^3 + 1) \cdot e^{4x}$

Ist die Funktion punktsymmetrisch in Bezug auf den Koordinatenursprung? Überprüfe!

Wir wollen die obige verschachtelte e-Funktion (Funktion mit e-Funktion, linearer Funktion im Exponenten und kubischer Funktion) auf Punktsymmetrie in Bezug auf den Koordinatenursprung überprüfen:

$-f(x) = f(-x)$ Punktsymmetrie

Wir betrachten zunächst die Ausgangsfunktion und setzen hier ein Minuszeichen vor die gesamte Funktion:

$-f(x) = - [(x^3 + 1) \cdot e^{4x}]$

$-f(x) = - (x^3 + 1) \cdot e^{4x}$

(1) $-f(x) = (-x^3 - 1) \cdot e^{4x}$

Danach setzen wir in die Ausgangsfunktion für x = -x ein:

$f(-x) = ((-x)^3 + 1) \cdot e^{4(-x)}$

Bei ungeraden Exponenten [wie z.B. (-x)³, -x] bleibt das Minuszeichen stehen [-x³]:

(2) $f(-x) = (-x^3 + 1) \cdot e^{-4x}$

Die Bedingung lautet nun, dass beide Funktionen (1) und (2) gleich sein müssen. In unserem Fall sind die beiden Funktionen nicht gleich:

$-f(x) \neq f(-x)$

Damit liegt für die gegebene Funktion keine Punktsymmetrie im Koordinatenursprung vor:

Punktsymmetrie bei e-Funktionen, Punktsymmetrie, e-Funktionen, e-Funktion

Drehst du den linken Teil der Funktion um 180° um den Koordinatenursprung, dann erhältst du nicht den rechten Teil der Funktion. Damit liegt hier keine Punktsymmetrie zum Koordinatenursprung vor.

Anwendung der Symmetrieanalyse

Mathematik: Verständnis von Funktionen und deren Transformationen.
Physik: Analyse von Wellenformen und exponentiellen Zerfallsprozessen.
Ingenieurwissenschaft: Untersuchung von Systemen, die exponentielles Wachstum oder Zerfall zeigen.

Mögliche Fragestellungen | Häufig gestellte Fragen (FAQs)

1. Was ist Punktsymmetrie?

Symmetrie liegt vor, wenn für jeden Punkt $(x, f(x))$ auf dem Graphen der Punkt $(2a - x, 2b - f(x))$ ebenfalls auf dem Graphen liegt.

2. Ist die Basis-e-Exponentialfunktion $f(x) = e^x$ punktsymmetrisch?

Nein, $f(x) = e^x$ ist weder achsensymmetrisch noch punktsymmetrisch zum Ursprung.

3. Wie überprüft man die Punktsymmetrie einer Funktion?

Setze $f(2a - x) = 2b - f(x)$ und überprüfe, ob die Bedingung für alle $x$ in der Domäne der Funktion erfüllt ist.

4. Kann eine verschobene e-Funktion punktsymmetrisch sein?

Eine verschobene e-Funktion wie $f(x) = e^x - k$ ist im Allgemeinen nicht punktsymmetrisch, es sei denn, sie erfüllt die spezifische Bedingung für Punktsymmetrie.

5. Warum ist Punktsymmetrie wichtig?

Die Angabe dieser Symmetrie hilft, das Verhalten und die Eigenschaften von Funktionen besser zu verstehen, insbesondere in der Analyse von Graphen und Transformationsprozessen.

Zusammenfassung

Die Überprüfung der Punktsymmetrie bei e-Funktionen und deren Modifikationen erfordert die Analyse der Bedingung $f(2a -x) = 2b - f(x)$ . Obwohl die Basis-e-Exponentialfunktion $f(x) = e^x$ nicht punktsymmetrisch ist, können modifizierte Funktionen interessante Symmetrieeigenschaften aufweisen.

Diese Analyse ist in Mathematik, Physik und Ingenieurwissenschaften von großer Bedeutung, um das Verhalten und die Struktur von Funktionen präzise zu verstehen.

Was kommt als Nächstes?

In der folgenden Lerneinheit zeigen wir dir, wie Ableiten mit der Produktregel abläuft.

Was gibt es noch bei uns?

Optimaler Lernerfolg durch tausende Übungsaufgaben

Übungsbereich (Demo) - Lerne mit mehr als 4000 Übungsaufgaben für deine Prüfungen — Übungsbereich (Demo) – Lerne mit mehr als 4000 Übungsaufgaben für deine Prüfungen

Quizfrage 1

Quizfrage 2

“Wusstest du, dass unter jedem Kursabschnitt eine Vielzahl von verschiedenen interaktiven Übungsaufgaben bereitsteht, mit denen du deinen aktuellen Wissensstand überprüfen kannst?”

Alle Technikerschulen im Überblick

Zum Verzeichnis der Technikerschulen (Alles Rund um die Schulen) — Zum Verzeichnis der Technikerschulen

Kennst du eigentlich schon unser großes Technikerschulen-Verzeichnis für alle Bundesländer mit allen wichtigen Informationen (Studiengänge, Kosten, Anschrift, Routenplaner, Social-Media) ? Nein? – Dann schau einfach mal hinein:

Was ist Technikermathe?

Unser Dozent Jan erklärt es dir in nur 2 Minuten!

Oder direkt den > kostenlosen Probekurs < durchstöbern? – Hier findest du Auszüge aus jedem unserer Kurse!

Geballtes Wissen in derzeit 26 Kursen

Hat dir dieses Thema gefallen? – Ja? – Dann schaue dir auch gleich die anderen Themen zu den Kursen

WT3 (Werkstoffprüfung) und
TM1 (Technische Mechanik – Statik) an.

Lerne nun erfolgreich mit unserem Onlinekurs Technische Mechanik 1 — TM1 (Technische Mechanik)

Lerne nun erfolgreich mit unserem Onlinekurs Werkstofftechnik 3 — WT3 (Werkstoffprüfung)

Perfekte Prüfungsvorbereitung für nur 14,90 EUR/Jahr pro Kurs

++ Günstiger geht’s nicht!! ++

Oder direkt Mitglied werden und Zugriff auf alle 26 Kurse (inkl. Webinare + Unterlagen) sichern ab 7,40 EUR/Monat ++ Besser geht’s nicht!! ++