In dieser Lerneinheit unseres Onlinekurses Ma3-Kurvendiskussion, wollen wir uns anschauen, wie die Nullstellen einer kubischen Funktion bestimmt werden.
Für ein optimales Verständnis helfen dir drei ausführliche Beispiele mit Zahlenwerten zu dem Thema. Mehr zu diesem Thema und der Mathematik findest du im Kurs: Onlinekurs MA3 – Kurvendiskussion. Oder lieber mit den Grundlagen starten? Alles dazu findest du im Kurs: Ma1-Grundlagen der MathematikDie Nullstellen von Funktionen sind die Schnittpunkte der Funktion mit der x-Achse. Der y-Wert ist an dieser Stelle Null.
Lernclips | Nullstellen ermitteln
sowie
Nullstellen bestimmen – Grundlagen
Kubische Funktion (Polynomdivision)?
Die Bestimmung der Nullstellen kubischer Funktionen ist ein zentrales Thema in der Mathematik und wird oft durch Polynomdivision und andere Techniken durchgeführt. Ein Kubische Funktion ist ein Polynom dritten Grades und hat die allgemeine Form ![]() . Das Finden der Nullstellen hilft, das Verhalten und die Struktur dieser Funktionen zu verstehen.
. Das Finden der Nullstellen hilft, das Verhalten und die Struktur dieser Funktionen zu verstehen.
Grundprinzipien
-
Definition von Nullstellen:
- Eine Nullstelle einer Funktion
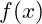 ist ein Wert
ist ein Wert 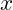 , für den
, für den 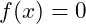 gilt.
gilt. - Eine Kubische Funktion kann bis zu drei Nullstellen haben.
- Eine Nullstelle einer Funktion
-
Kubische Funktion:
- Eine kubische Funktion hat die Form
 , wobei
, wobei 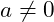 .
.
- Eine kubische Funktion hat die Form
Nullstellen ermitteln (bei kubischen Funktionen)
Eine Nullstelle ist dann gegeben, wenn die Funktion die x-Achse schneidet. Damit ist der y-Wert (=Funktionswert) an dieser Stelle gleich Null: f(x) = 0.
Die Bedingung für eine Nullstelle ist also, dass der Funktionswert zu Null wird. Zur Bestimmung der Nullstellen von Funktionen müssen wir also die gegebene Funktion gleich Null setzen und dann nach x auflösen. Wir ermitteln so die Stelle für x, bei welchem die Funktion zu Null wird. Damit liegt für diese Stelle eine Nullstelle vor.
Bei kubischen Funktionen haben wir zwei Möglichkeiten, um die Nullstellen zu bestimmen. In der vorangegangenen Lerneinheit haben wir uns bereits angeschaut, wie die Nullstellen einer kubischen Funktion ohne absolutes Glied berechnet werden. Jetzt betrachten wir eine kubische Funktion mit absolutem Glied.
Nullstelle bestimmen (mit absolutem Glied)
- Funktion gleich Null setzen: f(x) = 0
- Erste Nullstelle durch Raten bestimmen.
- Polynomdivision durchführen.
- p/q-Formel oder Mitternachtsformel anwenden.
Die Anzahl der Nullstellen wird durch den höchsten Exponenten festgelegt. Bei kubischen Funktionen (x²) gibt es drei Nullstellen der Funktion.
Kubische Funktionen mit absolutem Glied
Das absolute Glied d einer kubischen Funktion ist das Glied ohne x-Wert:
f(x) = ax³ + bx² + cx + d
Ist das absolute Glied gegeben, so können wir die Nullstellen einer Funktion mittels Polynomdivision bestimmen. Hierbei solltet ihr wissen, wie eine schriftliche Division durchgeführt wird.
Erste Nullstelle raten
Die erste Nullstelle wird durch raten bestimmt. Dazu setzt du in die Funktion verschiedene Werte ein, bis diese zu Null wird. Häufig sind Nullstellen bei 3,2,1,0,-1,-2,-3 gegeben.
Es gibt natürlich kubische Funktionen, bei denen die Nullstellen nicht ganzzahlig sind. Diese kannst du dann aber auch nicht raten. Wenn du eine Aufgabe erhältst, in welcher du die Nullstellen einer kubischen Funktion bestimmen sollst, dann gibt es eine Nullstelle, die du leicht raten kannst und die ganzzahlig ist. Ansonsten würdest du die Aufgabe in der Prüfung bzw. in Übungen nicht gestellt bekommen.
Vorgehensweise: Nullstellen bestimmen bei kubische Funktionen mit absolutem Glied
Gegeben sei die folgende kubische Funktion:
![]()
Bestimme die Nullstellen der Funktion!
Nullstelle raten
Zunächst bestimmen wir nun die 1. Nullstelle der Funktion, indem wir verschiedene Werte einsetzen:
![]()
Wir haben die erste Nullstelle bei x = 1 gefunden, weil hier der Funktionswert zu Null wird. Damit liegt ein Schnittpunkt mit der x-Achse vor.
Im nächsten Schritt wenden wir die Polynomdivision an.
Polynomdivision durchführen
Für die Polynomdivision benötigst du die Kenntnis über die schriftliche Division. Wir betrachten die gefundene Nullstelle x=1 und stellen die Gleichung so um, dass auf einer Seite = 0 steht:
![]() |-1
|-1
![]()
Wir können jetzt die linke Seite verwenden, um die Polynomdivision durchzuführen. Dazu schreiben wir die gegebene kubische Funktion auf und teilen durch x-1. Das sieht dann wie folgt aus:
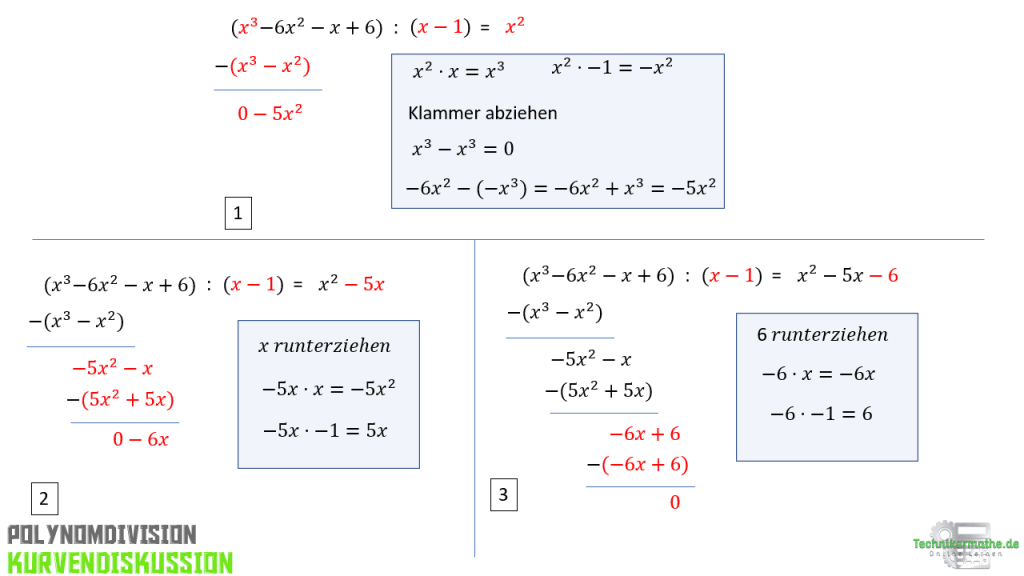
Wir sehen in der obigen Grafik, wie die Polynomdivision durchgeführt wird.
Zunächst schreibst du die Funktion (x³-6x²-x+6) in Klammern auf und dividierst davon (x-1). Hier geht jetzt die schriftliche Division los.
Hier erneut der Videoclip für ein besseres Verständnis zur Polynomdivision.
Wichtig bei der Polynomdivision ist es, dass am Ende 0 resultiert, also nach der schriftlichen Division kein Rest mehr verbleibt.
Wir haben dann eine quadratische Funktion als Ergebnis:
![]()
Wir können die Nullstellen dieser verbliebenen quadratische Funktion mittels p/q-Formel oder Mitternachtsformel berechnen.
p/q-Formel anwenden
![]()
mit
![]()
![]()
Wir berechnen als nächstes die Nullstellen:
![]()
![]()
![]()
![]()
Wir haben zwei weitere Nullstellen bei x2 = 6 und x3 = -1 gegeben. Insgesamt ergeben sich die folgenden Schnittpunkte mit der x-Achse:
S1(1|0), S2(6|0), S3(-1|0)
In der folgenden Grafik siehst du die kubische Funktion und ihre Nullstellen eingezeichnet:
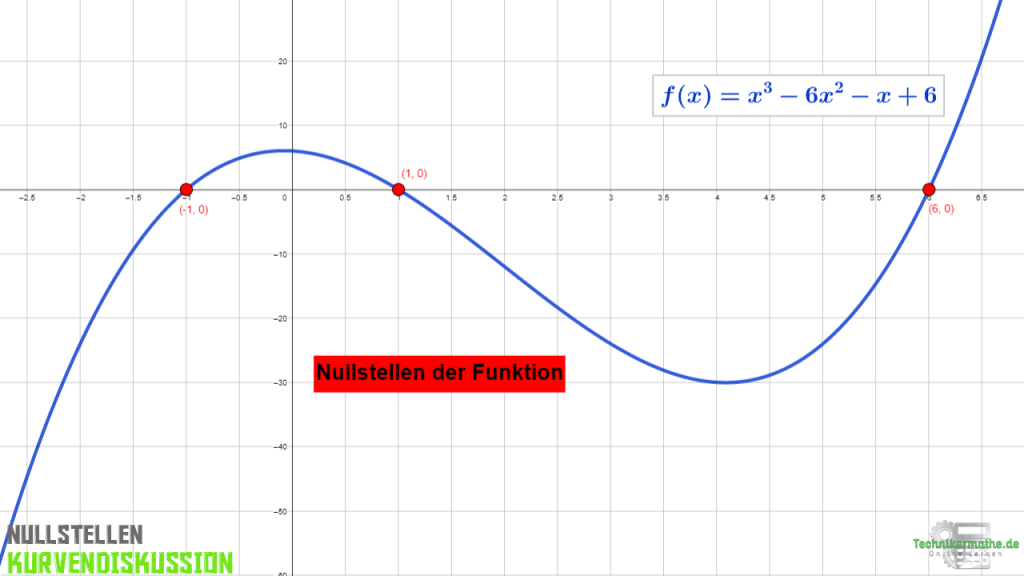
Anwendung der Polynomdivision
- Mathematik: Lösung von Polynomgleichungen höheren Grades.
- Ingenieurwissenschaft: Analyse von mechanischen Systemen und Schwingungen.
- Physik: Untersuchung von Bewegungs- und Kraftverläufen in komplexen Systemen.
Mögliche Fragestellungen | Häufig gestellte Fragen (FAQs)
1. Was ist eine Nullstelle?
Eine Nullstelle ist ein Punkt, an dem der Funktionswert null ist.
2. Wie findet man Nullstellen kubischer Funktionen?
Durch Raten einer möglichen Nullstelle, Polynomdivision und Lösen des resultierenden quadratischen Polynoms.
3. Was ist Polynomdivision?
Polynomdivision ist eine Methode zur Division von Polynomen, ähnlich wie bei der Division von Zahlen.
4. Kann jede kubische Funktion durch Polynomdivision gelöst werden?
Ja, jede kubische Funktion kann durch Polynomdivision gelöst werden, nachdem eine Nullstelle gefunden wurde.
5. Gibt es andere Methoden zur Bestimmung von Nullstellen?
Ja, neben der Polynomdivision gibt es Methoden wie numerische Verfahren (z.B. Newton-Verfahren) und spezielle Formeln für kubische Gleichungen.
Zusammenfassung
Die Bestimmung der Nullstellen kubischer Funktionen durch Polynomdivision ist eine grundlegende Technik in der Mathematik.
Durch das Raten einer Nullstelle, die Durchführung der Polynomdivision und das Lösen des resultierenden quadratischen Polynoms können alle Nullstellen der Funktion gefunden werden.
Diese Methode ist in vielen Bereichen wie Mathematik, Ingenieurwissenschaften und Physik von großer Bedeutung und hilft, das Verhalten und die Struktur komplexer Systeme zu verstehen.
In der folgenden Lerneinheit zeigen wir dir, wie Ableiten mit der Produktregel abläuft.
Was gibt es noch bei uns?
Optimaler Lernerfolg durch tausende Übungsaufgaben

Quizfrage 1
Quizfrage 2
“Wusstest du, dass unter jedem Kursabschnitt eine Vielzahl von verschiedenen interaktiven Übungsaufgaben bereitsteht, mit denen du deinen aktuellen Wissensstand überprüfen kannst?”
Was ist Technikermathe?
Unser Dozent Jan erklärt es dir in nur 2 Minuten!
Oder direkt den > kostenlosen Probekurs < durchstöbern? – Hier findest du Auszüge aus jedem unserer Kurse!
Geballtes Wissen in derzeit 26 Kursen
Hat dir dieses Thema gefallen? – Ja? – Dann schaue dir auch gleich die anderen Themen zu den Kursen
WT3 (Werkstoffprüfung) und
TM1 (Technische Mechanik – Statik) an.


Perfekte Prüfungsvorbereitung für nur 14,90 EUR/Jahr pro Kurs
++ Günstiger geht’s nicht!! ++
Oder direkt Mitglied werden und Zugriff auf alle 26 Kurse (inkl. Webinare + Unterlagen) sichern ab 7,40 EUR/Monat ++ Besser geht’s nicht!! ++
Social Media? - Sind wir dabei!
Dein Technikermathe.de-Team






