MA3 – Nullstellen bei gebrochenrationalen Funktionen [Grundlagen, Aufgaben, Tipps]

In dieser Lerneinheit schauen wir uns an, wie die Nullstellen bei gebrochenrationalen Funktionen ermittelt werden.

Für ein optimales Verständnis helfen dir drei ausführliche Beispiele mit Zahlenwerten zu dem Thema.

Mehr zu diesem Thema und der Mathematik findest du im Kurs: Onlinekurs MA3 – Kurvendiskussion.

Oder lieber mit den Grundlagen starten? Alles dazu findest du im Kurs: Ma1-Grundlagen der Mathematik

Nullstellen | Grundlagen

Was sind die Nullstellen einer Funktion?

Nullstellen einer Funktion sind die Punkte, an denen die Funktion den Wert null annimmt. Das Bestimmen von Nullstellen ist ein fundamentales Konzept in der Mathematik und hat weitreichende Anwendungen in vielen Bereichen wie der Physik, Ingenieurwissenschaften und Wirtschaft.

Grundprinzipien

Definition der Nullstellen:
- Eine Nullstelle einer Funktion 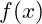$f(x)$ ist ein Wert $x_0$ , für den gilt $f(x) = 0$ .
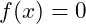- Mathematisch ausgedrückt: $x_0$ ist eine Nullstelle, wenn $f(x_0) = 0$ .
Typen von Nullstellen:
- Einfache Nullstellen: Nullstellen, bei denen die Funktion die x-Achse kreuzt.
- Mehrfache Nullstellen: Nullstellen, bei denen die Funktion die x-Achse berührt und nicht kreuzt.

Schritte zur Bestimmung der Nullstellen

Funktion gleich Null setzen: Setze die Funktion gleich Null und löse die resultierende Gleichung: $f(x) = 0$ .
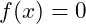Analytische Methoden:
- Lineare Funktionen: Für $f(x) = m \cdot x +b$ , löse $m \cdot x + b = 0$ durch Umstellen nach $x$ .
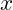- Quadratische Funktionen: Für $F(x) = a \cdot x^2 + b \cdot x + c$ , verwende die Mitternachtsformel (quadratische Lösungsformel): $x = \frac{ - b \pm \sqrt{b^2 - 4ac}}{2a}$
- Polynomfunktionen höherer Grade: Verwende Faktorisierung, Polynomdivision oder numerische Methoden.
Numerische Methoden:
- Newton-Verfahren: Iteratives Verfahren zur näherungsweisen Bestimmung von Nullstellen.
- Bisektionsmethode: Teilt das Intervall iterativ, um die Nullstelle zu finden.
Graphische Methode: Zeichne den Graphen der Funktion und identifiziere die Punkte, an denen der Graph die x-Achse schneidet.

Eine Nullstelle ist also dann gegeben, wenn die gebrochenrationale Funktion die x-Achse schneidet. Damit ist der y-Wert (=Funktionswert) an dieser Stelle gleich Null: f(x) = 0.

Nullstellen | gebrochenrationale Funktion

Eine Nullstelle ist dann gegeben, wenn die Funktion die x-Achse schneidet. Damit ist der y-Wert (=Funktionswert) an dieser Stelle gleich Null: f(x) = 0.

Die Bedingung für eine Nullstelle ist also, dass der Funktionswert zu Null wird. Bei gebrochenrationalen Funktionen wird dazu die Zählerfunktion p(x) gleich Null gesetzt und nach x aufgelöst. Wird der Zähler zu Null, so wird auch die gesamte Funktion zu Null. Damit liegt für diese Stelle eine Nullstelle vor.

Nullstelle bestimmen

Zählerfunktion gleich Null setzen: p(x) = 0
Zählerfunktion nach x auflösen durch Anwendung der p/q-Formel oder der Mitternachtsformel.
Gefundene Nullstellen in die Nennerfunktion q(x) einsetzen:
Ergebnis = 0 (keine Nullstelle der Funktion)
Ergebnis ≠ 0 (Nullstelle der Funktion).

Merk’s dir!

Zur Bestimmung der Nullstelle einer gebrochenrationalen Funktion, wird die Zählerfunktion gleich Null gesetzt und nach x aufgelöst.

Schauen wir uns dazu mal ein Beispiel an. In der folgenden Grafik siehst du eine gebrochen rationale Funktion, für welche die Nullstellen (Schnittpunkte mit der x-Achse) angegeben sind:

Nullstellen bei gebrochenrationalen Funktionen, Nullstellen, gebrochen rationale Funktion, Zählernullstelle

An den Stellen x₁ = 2,281 und x₂ = 0,219 schneidet die Funktion die x-Achse und der Funktionswert wird zu Null. Die Nullstellen einer gebrochenrationalen Funktion bestimmst du, indem du die Zählerfunktion gleich Null setzt und die 0-Stellen berechnest. In diesem Beispiel ist die Zählerfunktion eine quadratische Funktion. Wir haben hier die 0-Stellen durch Anwendung der Mitternachtsformel ermittelt.

Wichtig: Bei gebrochenrationalen Funktionen musst du zusätzlich überprüfen, ob die Nullstellen der Zählerfunktion auch Nullstellen der Nennerfunktion sind. Nur wenn die Zählernullstellen nicht auch Nullstellen des Nenners sind, liegen auch tatsächlich Nullstellen der Funktion vor. Wird der Nenner zu Null, so ist an dieser Stelle eine Definitionslücke der Funktion gegeben.

Wir wollen uns nun anhand eines ausführlichen Beispiels anschauen, wie du die obigen 0-Stellen rechnerisch ermittelst.

Beispiel!

$f(x) = \frac{2x^2 - 5x + 1}{4x^3 + 10}$

Bestimme die 0-Stellen der gegebenen Funktion!

Wir haben eine gebrochenrationale Funktion gegeben und wollen die Nullstellen der Funktion bestimmen. Bei gebrochenrationalen Funktionen werden die 0-Stellen bestimmt, indem die Funktion im Zähler gleich Null gesetzt wird. Wird der Zähler zu Null, so wird die gesamte Funktion zu Null. Damit liegt eine Nullstelle der Funktion vor:

Zählerfunktion

$p(x) = 2x^2 - 5x + 1$

Wir setzen die Zählerfunktion gleich Null und lösen nach x auf:

$p(x) = 2x^2 - 5x + 1 = 0$

Um die quadratische Funktion nach x auflösen zu können, benötigen wir die Mitternachtsformel:

$x_{1,2} = \frac{-b \pm \sqrt{b^2 - 4 \cdot a \cdot c}}{2 \cdot a}$

Für unsere Funktion gilt:

Nullstellen bei gebrochenrationalen Funktionen, Nullstellen, gebrochenrationale Funktion, Beispiel, Mitternachtsformel

Wir haben also gegeben:

$a = 2$ , $b = -5$ und $c = 1$

Wir setzen die Werte in die Mitternachtsformel ein:

$x_{1,2} = \frac{-(-5) \pm \sqrt{(-5)^2 - 4 \cdot 2 \cdot 1}}{2 \cdot 2}$

$x_{1} = \frac{5 + \sqrt{17}}{4} = 2,281$

$x_{2} = \frac{5 - \sqrt{17}}{4} = 0,219$

Wir haben die 0-Stellen der Funktion bei x = 2,281 und bei x = 0,219 gegeben. Wir müssen aber auch überprüfen, ob bei eine dieser 0-Stellen der Nenner zu Null wird. Dann liegt für diesen x-Wert keine Nullstelle vor, weil dann eine Definitionslücke gegeben ist.

Die Nennerfunktion lautet wie folgt:

$p(x) = 4x^3 + 10$

Wir setzen nun die beiden 0-Stellen in die Nennerfunktion ein:

$q(x = 2,281) = 4 \cdot 2,281^3 + 10 = 57,47 \neq 0$

$q(x = 0,219) = 4 \cdot 0,219^3 + 10 = 510,04 \neq 0$

Da der Nenner bei keinem der x-Werte zu Null wird, sind beide gefundenen x-Werte aus der Zählerfunktion auch 0-Stellen der Funktion:

$x_1 = 0,219$

$x_2 = 2,281$

Damit liegen die Schnittpunkte mit der x-Achse bei:

S(0,219 | 0)

H(2,281 | 0)

Wir haben die Nullstellen der gebrochen rationalen Funktion ermittelt.

Anwendung der Nullstellen

Mathematik: Lösung von Gleichungen, Analyse von Funktionen.
Physik: Bestimmung von Gleichgewichtspunkten, Analyse von Schwingungen.
Wirtschaft: Berechnung von Break-even-Punkten, Optimierung von Gewinnfunktionen.

Mögliche Fragestellungen | Häufig gestellte Fragen (FAQs)

1. Was ist eine Nullstelle?

Eine Nullstelle ist ein Punkt $x_0$ , an dem die Funktion den Wert null annimmt, also $f(x) = 0$ .

2. Wie finde ich Nullstellen einer Funktion?

Setze die Funktion gleich Null und löse die resultierende Gleichung durch analytische oder numerische Methoden.

3. Was ist der Unterschied zwischen einfachen und mehrfachen Nullstellen?

Einfache Stellen sind Punkte, an denen die Funktion die x-Achse kreuzt. Mehrfache Stellen sind Punkte, an denen die Funktion die x-Achse berührt, aber nicht kreuzt.

4. Welche Methoden gibt es zur Bestimmung von Nullstellen?

Analytische Methoden (Lösen von Gleichungen, Mitternachtsformel), numerische Methoden (Newton-Verfahren, Bisektionsmethode) und graphische Methoden (Zeichnen des Graphen).

5. Warum sind Nullstellen wichtig?

Nullstellen sind wichtig für die Analyse und Lösung von Gleichungen, die Untersuchung von Funktionen und die Anwendung in verschiedenen wissenschaftlichen und technischen Disziplinen.

Zusammenfassung

Die Kettenregel ist ein essentielles Werkzeug in der Differentialrechnung zur Berechnung der Ableitung zusammengesetzter Funktionen.

Durch die Identifikation der inneren und äußeren Funktionen und deren Ableitungen ermöglicht die Regel eine systematische und effiziente Bestimmung der gesuchten Ableitung.

Sie ist in vielen Bereichen der Mathematik und angewandten Wissenschaften von großer Bedeutung und wird häufig verwendet, um komplexe Differenzierungsprobleme zu lösen.

Was kommt als Nächstes?

In der folgenden Lerneinheit zeigen wir dir, wie Ableiten mit der Produktregel abläuft.

Was gibt es noch bei uns?

Optimaler Lernerfolg durch tausende Übungsaufgaben

Übungsbereich (Demo) - Lerne mit mehr als 4000 Übungsaufgaben für deine Prüfungen — Übungsbereich (Demo) – Lerne mit mehr als 4000 Übungsaufgaben für deine Prüfungen

Quizfrage 1

Quizfrage 2

“Wusstest du, dass unter jedem Kursabschnitt eine Vielzahl von verschiedenen interaktiven Übungsaufgaben bereitsteht, mit denen du deinen aktuellen Wissensstand überprüfen kannst?”

Alle Technikerschulen im Überblick

Zum Verzeichnis der Technikerschulen (Alles Rund um die Schulen) — Zum Verzeichnis der Technikerschulen

Kennst du eigentlich schon unser großes Technikerschulen-Verzeichnis für alle Bundesländer mit allen wichtigen Informationen (Studiengänge, Kosten, Anschrift, Routenplaner, Social-Media) ? Nein? – Dann schau einfach mal hinein:

Was ist Technikermathe?

Unser Dozent Jan erklärt es dir in nur 2 Minuten!

Oder direkt den > kostenlosen Probekurs < durchstöbern? – Hier findest du Auszüge aus jedem unserer Kurse!

Geballtes Wissen in derzeit 26 Kursen

Hat dir dieses Thema gefallen? – Ja? – Dann schaue dir auch gleich die anderen Themen zu den Kursen

WT3 (Werkstoffprüfung) und
TM1 (Technische Mechanik – Statik) an.

Lerne nun erfolgreich mit unserem Onlinekurs Technische Mechanik 1 — TM1 (Technische Mechanik)

Lerne nun erfolgreich mit unserem Onlinekurs Werkstofftechnik 3 — WT3 (Werkstoffprüfung)

Perfekte Prüfungsvorbereitung für nur 14,90 EUR/Jahr pro Kurs

++ Günstiger geht’s nicht!! ++

Oder direkt Mitglied werden und Zugriff auf alle 26 Kurse (inkl. Webinare + Unterlagen) sichern ab 7,40 EUR/Monat ++ Besser geht’s nicht!! ++