In dieser Lerneinheit wollen wir uns das Monotonieverhalten einer verschachtelten e-Funktion anschauen.
Für ein optimales Verständnis helfen dir drei ausführliche Beispiele mit Zahlenwerten zu dem Thema. Mehr zu diesem Thema und der Mathematik findest du im Kurs: Onlinekurs MA3 – Kurvendiskussion. Oder lieber mit den Grundlagen starten? Alles dazu findest du im Kurs: Ma1-Grundlagen der Mathematik
Monotonieverhalten | Grundlagen
Das Monotonieverhalten einer Funktion sagt etwas über ihre Steigung aus. Ändert die Funktion ihr Verhalten, dann wechselt die Funktion von einer steigenden in eine fallende Funktion bzw. umgekehrt. Wichtig ist also die 1.Ableitung der Funktion, welche die Steigung der Funktion wiedergibt. Ist die Steigung positiv, so steigt die Funktion. Ist die Steigung negativ, so fällt die Funktion.
Was ist das Monotonieverhalten?
Das Monotonieverhalten einer Funktion beschreibt, wie sich die Funktion in Bezug auf steigende oder fallende Werte verhält. Das Verständnis des Monotonieverhaltens ist grundlegend in der Analysis und hat vielfältige Anwendungen in Mathematik, Wirtschaft und Naturwissenschaften.
Grundprinzipien
-
Definition des Monotonieverhaltens:
- Eine Funktion
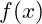 heißt monoton steigend auf einem Intervall, wenn für alle
heißt monoton steigend auf einem Intervall, wenn für alle  in diesem Intervall gilt:
in diesem Intervall gilt:  .
. - Eine Funktion
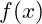 heißt streng monoton steigend, wenn für alle
heißt streng monoton steigend, wenn für alle  in diesem Intervall gilt:
in diesem Intervall gilt: 
- Analog gilt, dass eine Funktion
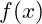 monoton fallend ist, wenn
monoton fallend ist, wenn  , und streng monoton fallend, wenn
, und streng monoton fallend, wenn  .
.
- Eine Funktion
-
Bedeutung der Ableitung:
- Eine Funktion
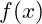 ist monoton steigend, wenn ihre erste Ableitung
ist monoton steigend, wenn ihre erste Ableitung  auf dem Intervall ist.
auf dem Intervall ist. - Eine Funktion
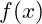 ist streng monoton steigend, wenn
ist streng monoton steigend, wenn  auf dem Intervall ist.
auf dem Intervall ist. - Eine Funktion
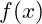 ist monoton fallend, wenn
ist monoton fallend, wenn  auf dem Intervall ist.
auf dem Intervall ist. - Eine Funktion
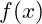 ist streng monoton fallend, wenn
ist streng monoton fallend, wenn  auf dem Intervall ist.
auf dem Intervall ist.
- Eine Funktion
Schritte zur Bestimmung des Monotonieverhaltens
-
Ableitung der Funktion berechnen: Berechne die erste Ableitung
 der Funktion
der Funktion 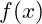 .
. -
Nullstellen der Ableitung finden: Löse die Gleichung
 , um kritische Punkte zu bestimmen, an denen sich das Monotonieverhalten ändern könnte.
, um kritische Punkte zu bestimmen, an denen sich das Monotonieverhalten ändern könnte. -
Vorzeichen der Ableitung untersuchen: Untersuche das Vorzeichen von
 in den Intervallen, die durch die kritischen Punkte bestimmt werden.
in den Intervallen, die durch die kritischen Punkte bestimmt werden. -
Monotonieintervalle bestimmen: Bestimme die Intervalle, in denen die Funktion monoton steigend oder fallend ist, basierend auf dem Vorzeichen der Ableitung.
Streng monoton fallend oder streng monoton steigend
Das Monotonieverhalten einer Funktion f(x) können wir über die 1. Ableitung der Funktion bestimmen:
-
Wenn f'(x) > 0 für alle x-Werte in einem Bereich ist, so ist die Funktion dort streng monoton steigend.
-
Wenn f'(x) < 0 für alle x-Werte in einem Bereich ist, so ist die Funktion dort streng monoton fallend.
Streng monoton steigend und fallend:
Eine Funktion heißt streng monoton steigend, wenn mit zunehmendem x-Wert der Funktionswert der Funktion immer ansteigt. Eine Funktion heißt streng monoton fallend, wenn mit zunehmendem x-Wert der Funktionswert der Funktion immer fällt.
Betrachten wir mal die folgende Grafik, in welcher anhand einer Funktion höheren Grades f(x) = 2x³ – 3x² das Monotonieverhalten aufgezeigt wird:

Die Funktion weist mehrere Bereiche auf.
Streng monoton steigend: Zunächst steigt die Funktion bis x = 0 an. Bei x = 0 weist die Funktion keine Steigung auf, damit ist die 1. Ableitung gleich Null.
Streng monoton fallend: Nach x = 0 fällt die Funktion bis x = 1. Damit ist sie hier streng monoton fallend. Bei x = 1 ist die 1. Ableitung gleich Null, damit liegt hier keine Steigung vor.
Streng monoton steigend: Nach x = 1 steigt die Funktion wieder an. Hier ist sie also streng monoton steigend.
Monotonieverhalten bestimmen (e-Funktion)
Gegeben sei die verschachtelte e-Funktion:
![]()
Bestimme das Monotonieverhalten der Funktion!
Wir wollen herausfinden, in welchen Bereichen die gegebene verschachtelte e-Funktion streng monoton steigend und streng monoton fallend ist. Wir haben hier eine e-Funktion mit linearer Funktionen im Exponenten sowie mit quadratischer Funktion in der Klammer gegeben.
Um herauszufinden, wo die Funktion monoton steigt und wo monoton fällt, müssen wir die 1.Ableitung bilden und diese gleich Null setzen. Ist die 1.Ableitung gleich Null, so weist die Funktion in diesem Punkt keine Steigung auf. Hier liegt bei einfacher Nullstelle bzw. bei ungerader Vielfachheit der Nullstelle (z.B. dreifache Nullstelle) ein Vorzeichenwechsel vor. Damit ändert die Funktion an dieser Stelle ihr Monotonieverhalten.
Um die 1.Ableitung zu bilden – siehe Lektion [Ma3-8-0] in diesem Onlinekurs – verwenden wir die Produkt- und Kettenregel.
Die Produktregel lautet:
![]()
![]()
Für unsere Funktion gilt:
![]()
![]()
![]()
Hier müssen wir noch die Kettenregel anwenden, indem wir den Exponenten ableiten und mit der gegebenen e-Funktion multiplizieren:
![]()
![]()
Wir können nun die Produktregel anwenden:
![]()
![]()
![]()
![]()
![]()
Wir können jetzt die Stelle bestimmen, an welcher die Steigung den Wert Null annimmt und damit keine Steigung gegeben ist. Dazu setzen wir die 1.Ableitung gleich Null und lösen nach x auf:
![]()
![]()
Hier wenden wir den Satz vom Nullprodukt an und betrachten beide Faktoren (Klammer und e-Funktion) separat.
e-Funktion
![]() |ln
|ln
![]() Abbruch, da ln(0) nicht definiert
Abbruch, da ln(0) nicht definiert
-> Hier gibt es keine Nullstelle!
Klammer
![]()
Hierbei handelt es sich um eine quadratische Funktion. Wir wenden hier die Mitternachtsformel an, um die x-Werte zu berechnen:
![]()
Hierbei gilt: ax² + bx + c
Hier ist:
![]() ,
, ![]() und
und ![]()
Einsetzen:



Bei x1 = -4,24 und x2 = 0,24 ist keine Steigung gegeben. Hier wird die 1.Ableitung gleich Null. Damit findet hier ein Vorzeichenwechsel statt und die Funktion wechselt ihr Monotonieverhalten. Wir müssen noch herausfinden, welches Monotonieverhalten die Funktion vor und nach diesen Stellen aufweist.
Dazu setzen wir einfach Werte vor diesen Stelle und nach diesen Stelle in die 1.Ableitung ein. Wir beginnen immer mit der kleinsten Stelle (hier: -4,24) und betrachten zunächst den Bereich davor.
Für x =-4,24 setzen wir -4,3 ein:
![]()
Da die Steigung hier negativ ist, ist die Funktion vor x = -4,24 streng monoton fallend.
Jetzt müssen wir auch wissen, wie sich die Funktion nach -4,24 verhält, aber noch vor dem nächsten ermittelten x-Wert, also zwischen -4,24 und 0,24.
Wir setzen hier beliebig einen Wert dazwischen ein z.B. x = -1:
![]()
Da die Steigung hier positiv ist, ist die Funktion zwischen -4,24 und 0,24 streng monoton steigend.
Den letzten Bereich, den wir ermitteln müssen, ist der Bereich nach 0,24.
Wir setzen x = 0,3 ein:
![]()
Da die Steigung hier negativ ist, ist die Funktion nach x = -0,17 streng monoton fallend.
Schauen wir uns die Funktion mal in der folgenden Grafik an:

Die Funktion weist mehrere Bereiche auf.
Streng monoton fallend: Zunächst fällt die Funktion bis x = -4,24. Bei x = -4,24 weist die Funktion keine Steigung auf, damit ist die 1. Ableitung gleich Null.
Streng monoton steigend: Nach x = -4,24 steigt die Funktion bis x = 0,24. Damit ist sie hier streng monoton steigend. Bei x = 0,24 ist die 1. Ableitung gleich Null, damit liegt hier keine Steigung vor.
Streng monoton fallend: Nach x = 0,24 fällt die Funktion wieder. Hier ist sie also streng monoton fallend.
Anwendung des Monotonieverhaltens
- Mathematik: Analyse von Funktionsverläufen, Untersuchung von Extrema.
- Wirtschaft: Optimierung von Gewinn- und Kostenfunktionen, Angebots- und Nachfragekurven.
- Physik: Modellierung von Bewegungen und Kräften, Analyse von Systemen.
Mögliche Fragestellungen | Häufig gestellte Fragen (FAQs)
1. Was bedeutet das Monotonieverhalten einer Funktion?
Das Monotonieverhalten beschreibt, ob und wie eine Funktion auf einem Intervall steigt oder fällt.
2. Wie finde ich das Monotonieverhalten einer Funktion?
Berechne die erste Ableitung der Funktion, finde die Nullstellen dieser Ableitung und untersuche das Vorzeichen der Ableitung in den verschiedenen Intervallen.
3. Warum ist das Monotonieverhalten wichtig?
Es hilft, das Verhalten von Funktionen zu verstehen, Extrema zu identifizieren und mathematische Modelle zu analysieren.
4. Kann eine Funktion in einem Intervall sowohl steigen als auch fallen?
Nein, in einem Intervall kann eine Funktion entweder monoton steigend, monoton fallend oder konstant sein.
5. Was passiert an den Nullstellen der Ableitung?
An den Nullstellen der Ableitung kann sich das Monotonieverhalten ändern, z.B. von steigend zu fallend oder umgekehrt.
Zusammenfassung
Das Monotonieverhalten einer Funktion ist ein wesentliches Konzept in der Mathematik, das beschreibt, wie sich eine Funktion in Bezug auf steigende oder fallende Werte verhält. Durch die Berechnung der ersten Ableitung und die Untersuchung ihrer Nullstellen kann das Monotonieverhalten einer Funktion bestimmt werden. Dies ist in vielen wissenschaftlichen und technischen Disziplinen von großer Bedeutung und hilft bei der Lösung komplexer Probleme und der Optimierung von Systemen.
In der folgenden Lerneinheit zeigen wir dir, wie Ableiten mit der Produktregel abläuft.
Was gibt es noch bei uns?
Optimaler Lernerfolg durch tausende Übungsaufgaben

Quizfrage 1
Quizfrage 2
“Wusstest du, dass unter jedem Kursabschnitt eine Vielzahl von verschiedenen interaktiven Übungsaufgaben bereitsteht, mit denen du deinen aktuellen Wissensstand überprüfen kannst?”
Was ist Technikermathe?
Unser Dozent Jan erklärt es dir in nur 2 Minuten!
Oder direkt den > kostenlosen Probekurs < durchstöbern? – Hier findest du Auszüge aus jedem unserer Kurse!
Geballtes Wissen in derzeit 26 Kursen
Hat dir dieses Thema gefallen? – Ja? – Dann schaue dir auch gleich die anderen Themen zu den Kursen
WT3 (Werkstoffprüfung) und
TM1 (Technische Mechanik – Statik) an.


Perfekte Prüfungsvorbereitung für nur 14,90 EUR/Jahr pro Kurs
++ Günstiger geht’s nicht!! ++
Oder direkt Mitglied werden und Zugriff auf alle 26 Kurse (inkl. Webinare + Unterlagen) sichern ab 7,40 EUR/Monat ++ Besser geht’s nicht!! ++
Social Media? - Sind wir dabei!
Dein Technikermathe.de-Team






