MA3 – Gebrochenrationale Funktion | Eigenschaften [Grundlagen, Video, Tipps]

In diesem Lerntext schauen wir uns an, was eine gebrochenrationale Funktion ist und welche Eigenschaften sie aufweist.

Für ein optimales Verständnis helfen dir ein Lernclip und drei ausführliche Beispiele mit Zahlenwerten zu dem Thema.

Mehr zu diesem Thema und der Mathematik findest du im Kurs: Onlinekurs MA3 – Kurvendiskussion.

Oder lieber mit den Grundlagen starten? Alles dazu findest du im Kurs: Ma1-Grundlagen der Mathematik

Gebrochenrationale Funktionen | Grundlagen

Eine Funktion f(x), deren Funktionsterm ein Quotient zweier Polynome p(x) und q(x) ist, wird als gebrochenrationale Funktion bezeichnet. Wir unterscheiden zwischen echt und unecht gebrochenrationalen Funktionen.

Was ist eine gebrochenrationale Funktion?

Gebrochenrationale Funktionen sind spezielle Funktionen, die als Bruch zweier Polynome definiert sind. Diese Funktionen treten häufig in verschiedenen Bereichen der Mathematik und Naturwissenschaften auf und bieten eine Vielzahl von Anwendungsmöglichkeiten und interessanten Eigenschaften.

Grundprinzipien

Definition einer gebrochenrationalen Funktion: Eine gebrochenrationale Funktion hat die Form:

$f(x) = \frac{P(x)}{Q(x)}$

wobei $P(x)$ und $Q(x)$ Polynome sind und $Q(x) \neq 0$ .
Eigenschaften:
Definitionsmenge: Die Werte von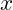 $x$ , für die $Q(x) \neq 0$ .

Asymptoten: Vertikale Asymptoten bei den Nullstellen von $Q(x)$ , horizontale oder schräge Asymptoten, abhängig vom Grad der Polynome $P(x)$ und $Q(x)$ .

Eine gebrochenrationale Funktion ist nichts anderes als der Quotient zweier ganzrationaler Funktionen p(x) und q(x):

Gebrochenrationale Funktion

$f(x) = \frac{p(x)}{q(x)}$

mit

$p(x) = a_nx^n + a_{n-1}x^{n-1} + ... +a_1x + a_0$

$q(x) = b_mx^m + b_{m-1}x^{m-1} + ... + b_1x + b_0$

Betrachten wir mal ein Beispiel für gebrochenrationale Funktionen:

$f(x) = \frac{5x^2 - 6x + 1}{2x^3 + 6x^2 - 7}$

Diese gebrochenrationale Funktion setzt sich zusammen aus einer quadratischen Funktion im Zähler und einer kubischen Funktion im Nenner.

Echt und unecht gebrochen rationale Funktionen

Betrachten wir gebrochenrationale Funktionen, so können wir echt gebrochen-rationale von unecht gebrochen-rationalen Funktionen unterscheiden. Dafür müssen wir den Grad des Zählers n und den Grad des Nenners m miteinander vergleichen.

Gebrochenrationale Funktion

Echt gebrochen-rationale Funktion

$n<m$ Zählergrad kleiner Nennergrad

Unecht gebrochen-rationale Funktion

$m<n$ Nennergrad kleiner Zählergrad

Betrachten wir hier zu mal zwei Beispiele:

$f(x) = \frac{0,6x^3 +5x^2 - 11}{x^5 + 3x - 5}$ Echt gebrochen-rationale Funktion

Hier ist der Zählergrad n = 3 und der Nennergrad m = 5. Damit gilt n<m und es liegt eine echt gebrochen rationale Funktion vor.

$f(x) = \frac{2x^4 - 6x + 5}{0,2x^3 + 4}$ Unecht gebrochen-rationale Funktion

Hier ist der Zählergrad n = 4 und der Nennergrad m = 3. Damit gilt m<n und es liegt eine unecht gebrochen rationale Funktion vor.

Polynomdivision

Bei einer unecht gebrochenen-rationalen Funktion kann die Funktion durch Anwendung der Polynomdivision in einen ganzrationalen Term und einen echt gebrochen-rationalen Term zerlegt werden.

Betrachten wir dazu ein Beispiel:

Beispiel!

Gegeben sei die folgenden unecht gebrochenrationale Funktion:

$f(x) = \frac{2x^4 - 6x + 5}{0,2x^3 + 4}$

Zeige, dass diese Funktion in einen ganzrationalen Term und einen echt gebrochenrationalen Term zerlegt werden kann!

Wir wenden hier die Polynomdivision an:

Polynomdivision, gebrochenrational, gebrochen-rational

Um die Polynomdivision anwenden zu können, musst du einfach den Zähler durch den Nenner teilen und hierbei die Polynomdivision anwenden. In dem folgenden Video erkläre ich dir, wie die Polynomdivision funktioniert.

In dem folgenden Video kannst du den Teil überspringen, bei dem ich die Nullstelle der Funktion suche. Wir haben den Teiler bereits gegeben (den Nenner). Für dich ist das Video ab Minute 4:58 relevant. Hier zeige ich die Durchführung der Polynomdivision.

Nachdem wir nun die Polynomdivision durchgeführt haben, siehst du, dass die folgende Funktion verbleibt:

$f(x) = 10x + \frac{-46x + 5}{0,2x^3 + 4}$

Diese Funktion setzt sich zusammen aus einer ganzrationalen Funktion (10x) und einer echt gebrochen-rationalen Funktion. Betrachten wir die gebrochen-rationale Funktion, so sehen wir, dass der Grad des Zählers n kleiner ist als der Grad des Nenners m. Damit gilt:

$n<m$ Echt gebrochen-rationale Funktion

Merk’s dir!

Ist der Zählergrad n größer als der Nennergrad m, so liegt eine unecht gebrochenrationale Funktion vor, die in einen ganzrationalen Anteil und einen echt gebrochenrationalen Anteil zerlegt werden kann.

Definitionsbereich: Gebrochenrationale Funktionen

Wir haben bereits ganzrationale Funktionen kennengelernt und wissen, dass diese für alle reellen Zahlen definiert sind. Bei gebrochenrationale Funktionen gehören nur die reellen Zahlen zum Definitionsbereich, für welche der Nenner q(x) nicht zu Null wird. Die Stelle bei welcher der Nenner zu Null wird (q(x) = 0) bezeichnen wir als Definitionslücken. An dieser Stelle bzw. an diesen Stellen ist die Funktion nicht definiert.

Betrachten wir hierzu ein Beispiel:

$f(x) = \frac{-4x + 5}{x^2 - 4}$

Für die obige gebrochenrationale Funktion ist der Definitionsbereich festzulegen. Dazu betrachten wir den Nenner der Funktion und schauen, wann dieser zu Null wird. In unserem Fall können wir also einfach die Nennerfunktion q(x) = 0 setzen und den x-Wert ermitteln:

$q(x) = x^2 - 4 = 0$ |nach x auflösen

$x^2 - 4 = 0$ |+4

$x^2 = 4$ |Wurzel

$x_{1,2} = \pm \sqrt{4} = \pm 2$

$x_1 = 2$

$x_2 = -2$

Setzen wir also x = 2 oder x = -2 in die Funktion ein, so wird der Nenner zu Null. Damit liegt hier eine Definitionslücke vor. Diese beiden x-Werte sind also nicht im Definitionsbereich enthalten. Damit gilt für den Definitionsbereich, dass dieser alle reellen Zahlen außer x = 2 und x = -2 enthält:

$D = \mathbb{R} \backslash \{2, -2\}$

In Worten: Der Definitionsbereich D umfasst alle reellen Zahlen ( $\mathbb R$ ), außer (\) die x-Werte 2 und -2.

Definitionslücken, gebrochenrationale Funktion, gebrochen-rationale Funktion

In der obigen Grafik siehst du die Funktion eingezeichnet. Bei x = -2 und x = 2 liegen Definitionslücken vor, da hier die Nennerfunktion zu Null wird. Die Funktion nähert sich diesen x-Werten immer weiter an, ohne sie jemals zu schneiden. Damit sind bei x = -2 und x = 2 Asymptoten der Funktion gegeben. Diese sind in rot als eingezeichnet.

Anwendung der gebrochenrationalen Funktionen

Mathematik: Untersuchung von Kurvenverläufen und Verhalten von Funktionen.
Physik: Modellierung von Bewegungen und Kräften, insbesondere bei Resonanzen und Dämpfung.
Ingenieurwissenschaften: Analyse von Regelkreisen und Übertragungsfunktionen.
Wirtschaft: Modellierung von Kosten- und Ertragsfunktionen.

Mögliche Fragestellungen | Häufig gestellte Fragen (FAQs)

1. Was ist eine gebrochenrationale Funktion?

Eine gebrochenrationale Funktion ist eine Funktion, die als Bruch zweier Polynome definiert ist.

2. Wie bestimme ich die Asymptoten einer gebrochenrationalen Funktion?

Vertikale Asymptoten entstehen bei den Nullstellen des Nenners $Q(x)$ . Horizontale oder schräge Asymptoten hängen vom Vergleich der Grade von Zähler $P(x)$ und Nenner $Q(x)$ ab.

3. Was sind die Nullstellen einer gebrochenrationalen Funktion?

Die Nullstellen sind die Werte von $x$ , für die der Zähler $P(x)$ gleich null ist, solange diese Werte den Nenner $Q(x)$ nicht ebenfalls null machen.

4. Warum sind gebrochenrationale Funktionen wichtig?

Sie bieten eine breite Palette an Modellierungsmöglichkeiten und treten in vielen naturwissenschaftlichen und technischen Kontexten auf.

5. Wie verhalte ich mich bei vertikalen Asymptoten?

Untersuche das Verhalten der Funktion nahe den vertikalen Asymptoten, indem du den Grenzwert der Funktion in der Nähe dieser Punkte analysierst.

Zusammenfassung

Gebrochenrationale Funktionen sind ein optimales Werkzeug zur Modellierung und Analyse komplexer Systeme in Mathematik und Naturwissenschaften.

Durch die Bestimmung der Definitionsmenge, das Finden von Nullstellen und Asymptoten sowie das Untersuchen des Verhaltens an den Rändern der Definitionsmenge kann das Verhalten dieser Funktionen umfassend analysiert werden.

Diese Methoden sind in vielen Disziplinen von großer Bedeutung und helfen bei der Lösung anspruchsvoller Probleme.

Was kommt als Nächstes?

In der folgenden Lerneinheit zeigen wir dir, wie die Linearfaktorzerlegung abläuft.

Was gibt es noch bei uns?

Optimaler Lernerfolg durch tausende Übungsaufgaben

Übungsbereich (Demo) - Lerne mit mehr als 4000 Übungsaufgaben für deine Prüfungen — Übungsbereich (Demo) – Lerne mit mehr als 4000 Übungsaufgaben für deine Prüfungen

Quizfrage 1

Quizfrage 2

“Wusstest du, dass unter jedem Kursabschnitt eine Vielzahl von verschiedenen interaktiven Übungsaufgaben bereitsteht, mit denen du deinen aktuellen Wissensstand überprüfen kannst?”

Alle Technikerschulen im Überblick

Zum Verzeichnis der Technikerschulen (Alles Rund um die Schulen) — Zum Verzeichnis der Technikerschulen

Kennst du eigentlich schon unser großes Technikerschulen-Verzeichnis für alle Bundesländer mit allen wichtigen Informationen (Studiengänge, Kosten, Anschrift, Routenplaner, Social-Media) ? Nein? – Dann schau einfach mal hinein:

Was ist Technikermathe?

Unser Dozent Jan erklärt es dir in nur 2 Minuten!

Oder direkt den > kostenlosen Probekurs < durchstöbern? – Hier findest du Auszüge aus jedem unserer Kurse!

Geballtes Wissen in derzeit 26 Kursen

Hat dir dieses Thema gefallen? – Ja? – Dann schaue dir auch gleich die anderen Themen zu den Kursen

WT3 (Werkstoffprüfung) und
TM1 (Technische Mechanik – Statik) an.

Lerne nun erfolgreich mit unserem Onlinekurs Technische Mechanik 1 — TM1 (Technische Mechanik)

Lerne nun erfolgreich mit unserem Onlinekurs Werkstofftechnik 3 — WT3 (Werkstoffprüfung)

Perfekte Prüfungsvorbereitung für nur 14,90 EUR/Jahr pro Kurs

++ Günstiger geht’s nicht!! ++

Oder direkt Mitglied werden und Zugriff auf alle 26 Kurse (inkl. Webinare + Unterlagen) sichern ab 7,40 EUR/Monat ++ Besser geht’s nicht!! ++