MA3 – Funktionsgleichung aufstellen | kubische Funktion [Grundlagen, Video, Tipps]

Wir wollen uns in dieser Lerneinheit anschauen, wie du die Funktionsgleichung aufstellen kannst, wenn bestimmte Eigenschaften einer Funktion gegeben sind. Eigenschaften einer Funktion können z. B. Wendepunkte, Nullstellen oder Extremwerte sein. Auch Tangenten, welche die Funktion berühren, können in der Aufgabenstellung gegeben sein. Ziel ist es die Koeffizienten der Funktion zu ermitteln, indem ein lineares Gleichungssystem aus den gegeben Eigenschaften aufgestellt wird.

Für ein optimales Verständnis helfen dir ein Lernclip und drei ausführliche Beispiele mit Zahlenwerten zu dem Thema.

Mehr zu diesem Thema und der Mathematik findest du im Kurs: Onlinekurs MA3 – Kurvendiskussion.

Oder lieber mit den Grundlagen starten? Alles dazu findest du im Kurs: Ma1-Grundlagen der Mathematik

Beispiel mit Lösung im Video: Funktionsgleichung aufstellen (Tangente, Schnittpunkt mit y-Achse, Steigung)

Beispiel!

Gesucht ist eine Polynomfunktion f(x) 3. Grades, die bei x_g = -2 durch eine Tangente mit der Funktionsgleichung g(x) ) -8x – 15 berührt wird. Die Funktion f(x) schneidet die y-Achse bei y0 = 1. Dort beträgt die Steigung m = 16.

Bestimme die Funktionsgleichung f(x)!

Lösung im Video

Funktionsgleichung aufstellen | Grundlagen

Warum eine Funktionsgleichung aufstellen?

Das Aufstellen einer Funktionsgleichung ist ein grundlegendes mathematisches Verfahren, das in vielen Bereichen Anwendung findet, darunter Naturwissenschaften, Wirtschaft und Ingenieurwesen. Eine Funktionsgleichung beschreibt die Beziehung zwischen unabhängigen und abhängigen Variablen in Form einer mathematischen Gleichung.

Grundprinzipien

Definition einer Funktion: Eine Funktion 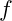$f$ ordnet jedem Element 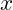$x$ aus der Definitionsmenge 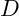$D$ genau ein Element 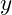$y$ aus der Wertemenge $W$ zu, d.h. $y = f(x)$
Typen von Funktionen:
- Lineare Funktion: $f(x) = mx + b$
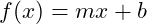
- Quadratische Funktion: $f(x) = a \cdot x^2 + b \cdot x + c$
- Exponentialfunktion: $f(x) = a \cdot e^{bx}$
- Kubische Funktion: $f(x) = a \cdot x^3 + b \cdot x^2 + c \cdot x + d$
- Logarithmische Funktion: $f(x) = a \cdot log_b (x)$

Schritte zum Aufstellen einer Funktionsgleichung

Identifikation des Funktionstyps: Bestimme, welche Art von Funktion vorliegt (linear, quadratisch, etc.), basierend auf der Problemstellung oder gegebenen Datenpunkten.
Sammeln von Informationen:
- Gegebene Punkte: Sammle gegebene Punkte
- Zusätzliche Bedingungen: Eventuell gegebene Steigungen, Extremwerte, Asymptoten oder andere spezifische Bedingungen.
Aufstellen des Gleichungssystems: Erstelle ein Gleichungssystem, das die gesammelten Punkte und Bedingungen erfüllt.
Lösen des Gleichungssystems: Löse das Gleichungssystem, um die unbekannten Parameter der Funktion zu bestimmen.
Funktionsgleichung aufstellen: Schreibe die Funktionsgleichung mit den gefundenen Parametern auf.

Klausuraufgabe | Funktionsgleichung aufstellen (Nullstelle, Wendestelle, Tangente)

Aufgabenstellung

Betrachtet wird ein Polynom 3. Grades mit einer Nullstelle bei x₀ = 1 und einer Wendestelle bei x_w = -1. Gegeben sei außerdem die Wendetangente mit der Gleichung g(x) = −9x + 1.

Bestimme die Funktionsgleichung f(x)!

Lösung

Funktionsgleichung aufstellen

Gesucht wird eine Funktion 3.Grades. Wir stellen zunächst die Funktionsgleichung in ihrer Normalform auf:

$f(x) = ax^3 + bx^2 + cx + d$ Ausgangsfunktion

Ableitungen bilden

Wir bilden zunächst die 1. und 2. Ableitung (die 3. Ableitung ist bei einer kubischen Funktion nicht mehr von x-abhängig und damit nicht relevant):

$f'(x) = 3ax^2 + 2bx + c$ 1.Ableitung

$f''(x) = 6ax + 2b$ 2.Ableitung

Die Nullstelle x₀ wird bei der Kurvendiskussion aus der Ausgangsfunktion bestimmt, indem diese gleich Null gesetzt und nach x aufgelöst wird:

$f(x_0) = ax_0^3 + bx_0^2 + cx_0 + d = 0$

Die Wendestelle x_w wird bei der Kurvendiskussion aus der 2. Ableitung bestimmt, indem diese gleich Null gesetzt und nach x aufgelöst wird:

$f''(x_w) = 6ax_w + 2b = 0$

Gleichungen aufstellen

Es müssen insgesamt n+1-Gleichungen, also 4-Gleichungen aufgestellt werden, um die 4 Koeffizienten a, b, c und d der kubischen Funktion zu berechnen.

Wir haben nun zwei Eigenschaften der Funktion gegeben. Zum einen die Nullstelle bei x₀ = 1 und zum anderen die Wendestelle bei x_w = -1.

Angaben zur Nullstelle

Die Nullstelle wird aus der Ausgangsfunktion bestimmt, indem diese gleich Null gesetzt wird. Wir setzen also die Nullstelle in die Ausgangsfunktion ein und setzen diese gleich Null:

$f(x_0 = 1) = a \cdot 1^3 + b \cdot 1^2 + c \cdot 1 + d = 0$

$a \cdot 1^3 + b \cdot 1^2 + c \cdot 1 + d = 0$

$a + b + c + d = 0$ Gleichung I

Angaben zur Wendestelle

Die Wendestelle wird aus der 2.Ableitung bestimmt, indem diese gleich Null gesetzt wird. Wir setzen also die Wendestelle in die 2.Ableitung ein und setzen diese gleich Null:

$f''(x_w = -1) = 6a \cdot (-1) + 2b = 0$

$-6a + 2b = 0$ Gleichung II

Angaben zur Wendetangente

Die Wendetangente g(x) = -9x+1 liegt – wie der Name bereits aussagt – an der Wendestelle bei x_w = -1 der Funktion f(x). Eine Wendetangente hat an dieser Stelle genau denselben Funktionswert und dieselbe Steigung wie die Funktion:

$f(x_w) = g(x_w)$ Gleicher Funktionswert an der Stelle

$f'(x_w) = g'(x_w)$ Gleiche Steigung an der Stelle

Wir setzen nun die Ausgangsfunktion und die Wendetangente gleich und setzen xw ein:

$a \cdot (-1)^3 + b \cdot (-1)^2 + c \cdot (-1) + d = -9 \cdot (-1) + 1$

$-a + b - c + d = 10$ Gleichung III

Hinweis: Wird eine negative Zahl mit einem ungeraden Exponenten potenziert,
so bleibt die Potenz negativ. (-1)³ = -1³ = -1

Betrachten wir als nächstes die Steigung. Die Steigung an der Stelle x_w = -1 entspricht der Steigung der Wendetangente an dieser Stelle. Die Steigung ist nichts anderes als die 1.Ableitung der Funktionen. Diese setzen wir gleich:

$f'(x_w) = g'(x_w)$

mit

$f'(x) = 3ax^2 + 2bx + c$

$g'(x) = -9$

Wir setzen die beiden Ableitungen gleich und setzen die Stelle x_w = -1 sein:

$3a \cdot x_w^2 + 2b \cdot x_w + c = -9$

$3a \cdot (-1)^2 + 2b \cdot (-1) + c = -9$

$3a - 2b + c = -9$ Gleichung IV

Wir haben insgesamt 4 Gleichungen aufgestellt, um die 4 unbekannten Koeffizienten zu berechnen.

Lineares Gleichungssystem aufstellen und lösen

Aus den aufgestellten Gleichungen können wir jetzt ein lineares Gleichungssystem aufstellen, indem wir die Gleichungen untereinander schreiben. Dabei setzen wir das Gleichheitszeichen für alle Gleichungen einheitlich auf die rechte Seite:

(1)	a	+	b	+	c	+	d	=	0
(2)	-6a	+	2b					=	0
(3)	-a	+	b	–	c	+	d	=	10
(4)	3a	–	2b	+	c			=	-9

Wir können das obige lineare Gleichungssystem mit einem beliebigen Verfahren lösen. Wir wenden hier die Additions- und Subtraktionsverfahren für lineare Gleichungssysteme so an, dass wir am Ende alle Koeffizienten berechnen können.

Betrachten wir die obigen Gleichungen, so können wir zum Beispiel die Variable d eliminieren, indem wir Gleichung (1) minus Gleichung (3) rechnen, da dann die Variable d wegfällt. Die anderen beiden Gleichungen weisen diese Variable nicht auf:

(1)	a	+	b	+	c	+	d	=	0
– (3)	-a	+	b	–	c	+	d	=	10
= (5)	2a			+	2c			=	-10

Wir haben nun eine neue Gleichung erhalten, in welche die Variable d nicht mehr vorkommt. Das neue Gleichungssystem ergibt sich wie folgt:

(2)	-6a	+	2b			=	0
(4)	3a	–	2b	+	c	=	-9
(5)	2a			+	2c	=	-10

Als nächstes können wir die Variable 2b entfernen, indem wir die Gleichung (2) plus Gleichung (4) rechnen:

(2)	-6a	+	2b			=	0
+ (4)	3a	–	2b	+	c	=	-9
= (6)	-3a			+	c	=	-9

Es ergibt sich als neues Gleichungssystem:

(5)	2a	+	2c	=	-10
(6)	-3a	+	c	=	-9

Wir wollen weiterhin das Additions- bzw. Subtraktionsverfahren anwenden. Das ist möglich, wenn wir die gesamte Gleichung (5) durch 2 dividieren. Dann erhalten wir für 2c = c und wir können hier wieder das Additionsverfahren anwenden:

(5):2

-5

Wir können nun Gleichung (5) minus (6) rechnen, so dass c wegfällt:

(5)	a	+	c	=	-5
– (6)	-3a	+	c	=	-9
= (7)	4a			=	4

Wir können nun beginnen die Koeffizienten zu berechnen. Aus der Gleichung (7) können wir a berechnen:

(7) $4a = 4$ |:4

$a = 1$

Aus der Gleichung (6) mit a = 1 können wir c berechnen:

(6) $-3a + c = -9$ |a = 1 einsetzen

$-3 \cdot 1 + c= -9$

$-3 + c = -9$ |+3

$c= -6$

Aus der Gleichung (4) können wir mit a = 1 und c = -6 den Koeffizienten b berechnen:

(4) $3a-2b+c=-9$

$3 \cdot 1 - 2b - 6 = -9$

$3 - 2b - 6 = -9$ |+6 |-3

$-2b = -6$ |:(-2)

$b = 3$

Aus der Gleichung (1) können wir mit a = 1, b = 3 und c = -6 den Koeffizienten d berechnen:

(1) $a + b + c + d = 0$

$1 + 3 - 6 + d = 0$

$-2 + d = 0$ |+2

$d = 2$

Wir haben alle Koeffizienten berechnet und können nun die Funktionsgleichung aufstellen:

$f(x) = x^3+ 3x^2 - 6x + 2$ Funktionsgleichung

Die Funktion sieht wie folgt aus:

Funktionsgleichung aufstellen, Nullstelle, Wendepunkt, Tangente

In der Aufgabenstellung war der Grad der Funktion (n = 3) sowie der die Nullstelle x₀ = 1, die Wendestelle x_w = -1 sowie die Wendetangente (Tangente an der Wendestelle) mit g(x) = -9x+1 gegeben. Aus diesen Eigenschaften haben wir die Funktionsgleichung ermittelt.

Anwendung der Funktionsgleichungen

Mathematik: Lösen von Problemen, die durch Funktionen beschrieben werden.
Physik: Modellierung von Bewegungen und Kräften.
Wirtschaft: Erstellung von Prognosen und Modellierung von Kosten und Erlösen.
Ingenieurwissenschaften: Analyse und Optimierung von Systemen.

Mögliche Fragestellungen | Häufig gestellte Fragen (FAQs)

1. Was ist eine Funktionsgleichung?

Eine Funktionsgleichung ist eine mathematische Gleichung, die die Beziehung zwischen unabhängigen und abhängigen Variablen beschreibt.

2. Wie stelle ich eine Funktionsgleichung auf?

Identifiziere den Funktionstyp, sammle Informationen (Datenpunkte, Bedingungen), erstelle ein Gleichungssystem, löse es und formuliere die Funktionsgleichung.

3. Welche Funktionstypen gibt es?

Lineare, quadratische, kubische, exponentielle, logarithmische und viele weitere Funktionen.

4. Warum sind Funktionsgleichungen wichtig?

Sie ermöglichen das mathematische Modellieren und Lösen von Problemen in verschiedenen Bereichen wie Naturwissenschaften, Wirtschaft und Technik.

5. Was mache ich, wenn ich mehr als zwei Punkte habe?

Bei mehr als zwei Punkten, die eine nicht-lineare Beziehung andeuten, solltest du einen höheren Grad des Polynoms in Betracht ziehen (z.B. quadratisch oder kubisch) und das entsprechende Gleichungssystem aufstellen und lösen.

Zusammenfassung

Das Aufstellen einer Funktionsgleichung ist ein essenzielles Verfahren zur mathematischen Modellierung und Analyse von Beziehungen zwischen Variablen.

Durch die Identifikation des Funktionstyps, das Sammeln relevanter Informationen, das Aufstellen und Lösen eines Gleichungssystems und das Formulieren der Funktionsgleichung kann man präzise Modelle erstellen, die in vielen wissenschaftlichen und technischen Disziplinen von großer Bedeutung sind.

Was kommt als Nächstes?

In der folgenden Lerneinheit zeigen wir dir, wie Ableiten mit der Produktregel abläuft.

Was gibt es noch bei uns?

Optimaler Lernerfolg durch tausende Übungsaufgaben

Übungsbereich (Demo) - Lerne mit mehr als 4000 Übungsaufgaben für deine Prüfungen — Übungsbereich (Demo) – Lerne mit mehr als 4000 Übungsaufgaben für deine Prüfungen

Quizfrage 1

Quizfrage 2

“Wusstest du, dass unter jedem Kursabschnitt eine Vielzahl von verschiedenen interaktiven Übungsaufgaben bereitsteht, mit denen du deinen aktuellen Wissensstand überprüfen kannst?”

Alle Technikerschulen im Überblick

Zum Verzeichnis der Technikerschulen (Alles Rund um die Schulen) — Zum Verzeichnis der Technikerschulen

Kennst du eigentlich schon unser großes Technikerschulen-Verzeichnis für alle Bundesländer mit allen wichtigen Informationen (Studiengänge, Kosten, Anschrift, Routenplaner, Social-Media) ? Nein? – Dann schau einfach mal hinein:

Was ist Technikermathe?

Unser Dozent Jan erklärt es dir in nur 2 Minuten!

Oder direkt den > kostenlosen Probekurs < durchstöbern? – Hier findest du Auszüge aus jedem unserer Kurse!

Geballtes Wissen in derzeit 26 Kursen

Hat dir dieses Thema gefallen? – Ja? – Dann schaue dir auch gleich die anderen Themen zu den Kursen

WT3 (Werkstoffprüfung) und
TM1 (Technische Mechanik – Statik) an.

Lerne nun erfolgreich mit unserem Onlinekurs Technische Mechanik 1 — TM1 (Technische Mechanik)

Lerne nun erfolgreich mit unserem Onlinekurs Werkstofftechnik 3 — WT3 (Werkstoffprüfung)

Perfekte Prüfungsvorbereitung für nur 14,90 EUR/Jahr pro Kurs

++ Günstiger geht’s nicht!! ++

Oder direkt Mitglied werden und Zugriff auf alle 26 Kurse (inkl. Webinare + Unterlagen) sichern ab 7,40 EUR/Monat ++ Besser geht’s nicht!! ++