In dieser Lerneinheit wollen wir uns anschauen, wie du die Extremwerte bestimmen kannst. Dazu betrachten wir eine kubische Funktion.
Für ein optimales Verständnis helfen dir zwei Videoclips und drei ausführliche Beispiele mit Zahlenwerten zu dem Thema. Mehr zu diesem Thema und der Mathematik findest du im Kurs: Onlinekurs MA3 – Kurvendiskussion. Oder lieber mit den Grundlagen starten? Alles dazu findest du im Kurs: Ma1-Grundlagen der Mathematik
Extremwerte bestimmen | Grundlagen
Die Extremwerte einer Funktion sind nichts anderes, als der höchste und tiefste Punkt der Funktion. Häufig wird auch vom Maximum und Minimum der Funktion gesprochen.
Extremwerte bestimmen
Das Bestimmen von Extremwerten einer Funktion ist ein wesentlicher Bestandteil der Analyse von mathematischen Modellen, insbesondere in der Optimierung und bei der Untersuchung von physikalischen Phänomenen. Extremwerte sind Punkte, an denen eine Funktion ihre höchsten oder niedrigsten Werte erreicht. Sie lassen sich in lokale und globale Extremwerte unterteilen.
Grundprinzipien
-
Definition von Extremwerten:
- Lokale Extremwerte: Ein Punkt
 ist ein lokales Maximum, wenn
ist ein lokales Maximum, wenn  für alle
für alle 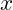 in einer Umgebung von
in einer Umgebung von  . Analog ist
. Analog ist  ein lokales Minimum, wenn
ein lokales Minimum, wenn  für alle
für alle 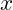 in einer Umgebung von
in einer Umgebung von  .
. - Globale Extremwerte: Ein Punkt
 ist ein globales Maximum, wenn
ist ein globales Maximum, wenn  für alle
für alle 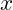 im Definitionsbereich. Analog ist
im Definitionsbereich. Analog ist  ein globales Minimum, wenn
ein globales Minimum, wenn  für alle
für alle 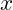 im Definitionsbereich.
im Definitionsbereich.
- Lokale Extremwerte: Ein Punkt
Vorgehensweise: Extremwerte
Zur Bestimmung der Extremwerte von Funktionen benötigen wir die 1. Ableitung und die 2. Ableitung der Funktion. Schauen wir uns mal an, wie die Extremwerte allgemein bestimmt werden.
Werte bestimmen
- Bilde die 1. Ableitung der Funktion und setze diese gleich Null: f'(x) = 0
- Löse die 1. Ableitung nach x auf. An dieser Stelle ist ein Minimum oder Maximum gegeben.
- Bilde die 2. Ableitung der Funktion. Setze den in 2. ermittelten x-Wert in die 2. Ableitung ein.
Ist der Wert größer Null, so liegt ein Minimum vor: f”(x) > 0 (Minimum)
Ist der Wert kleiner Null, so liegt ein Maximum vor: f”(x) < 0 (Maximum) - Setze den ermittelten x-Wert aus 2. in die Ausgangsfunktion f(x) ein, um den dazugehörigen y-Wert zu bestimmen.
Videos: Extremwerte bei kubischen Funktionen
Zum besseren Verständnis der Vorgehensweise schauen wir uns ein Beispiel an.
Vorgehensweise: Extremwerte bestimmen
Gegeben sei die folgende kubische Funktion:
![]()
Bestimme die Extremwerte der Funktion!
Erste Ableitung bilden und nach x auflösen
Wir starten mit der 1. Ableitung der Funktion:
![]()
Um einen Extremwert zu finden, muss die erste Ableitung gleich Null gesetzt werden. Die 1. Ableitung ist nichts anderes als die Steigung der Funktion. Ist ein Extremwert gegeben, so ist in diesem Punkt die Ableitung gleich Null.
Wir setzen die 1.Ableitung gleich Null und lösen nach x auf:
![]()
Da wir eine quadratische Funktion gegeben haben, können wir die x-Werte mittels p/q-Formel oder Mitternachtsformel berechnen.
p/q-Formel
![]()
Bei der Anwendung der p/q-Formel muss a = 1 sein. Da a = 3 gegeben ist, müssen wir die Funktion noch durch 3 teilen:
![]() |:3
|:3
![]()
Damit ergibt sich p = -4 und q = -1/3.
Wir berechnen als nächstes die x-Werte der 1-Ableitung:
![]()
![]()
![]()
![]()
An diesem Stellen liegen gegebenenfalls Extremwerte vor. Um herauszufinden, ob ein Maximum oder Minimum gegeben ist, müssen wir die beiden ermittelten x-Werte in die zweite Ableitung einsetzen.
Zweite Ableitung bilden
Wir bilden die 2. Ableitung der Funktion. Dazu leitest du einfach die 1. Ableitung ab:
![]()
![]()
Bei kubischen Funktionen ergibt sich bei der 2. Ableitung immer eine Funktion in Abhängigkeit von x. Um herauszufinden, ob ein Maximum oder Minimum gegeben ist, müssen wir als nächstes die ermittelten x-Werte einsetzen.
![]() > 0 ⇒ Minimum
> 0 ⇒ Minimum
![]() < 0 ⇒ Maximum
< 0 ⇒ Maximum
Bei x = 4,08 ist ein Minimum gegeben, da die 2.Ableitung größer Null ist. Bei x = -0,08 ist ein Maximum gegeben, da die 2.Ableitung kleiner Null ist.
Funktionswert berechnen
Wir müssen nun noch herausfinden, wie der dazugehörige y-Wert für das Minimum und Maximum aussieht. Dazu setzen wir den ermittelten x-Werte in die Ausgangsfunktion ein:
![]()
![]()
Wir können jetzt den Punkt des Minimums (=Tiefpunkt) und des Maximums (=Hochpunkt) angeben:
T(4,08 | -30,04)
H(-0,08 | 6,04)
In der folgenden Grafik sieht du die Funktion mit Hoch- und Tiefpunkt sowie den Nullstellen, die wir im vorangegangenen Abschnitt bestimmt haben:

Erläuterung zu den Hoch- und Tiefpunkten:
- Vor einem Hochpunkt steigt die Funktion an (positive Steigung), danach fällt sie ab (negative Steigung).
- Vor einem Tiefpunkt fällt die Funktion (negative Steigung), danach steigt die Funktion an (positive Steigung).
- Dort wo Hoch- oder Tiefpunkte gegeben sind, ist die Steigung der Funktion gleich Null (es liegt dort keine Steigung vor).
- Ist die 2. Ableitung nach Einsetzen der x-Werte gleich Null (=0), so liegt kein Extremwert, sondern ein Sattelpunkt vor.
Anwendung der Extremwertanalyse
- Mathematik: Optimierung und Funktionsanalyse.
- Wirtschaft: Maximierung von Gewinn oder Minimierung von Kosten.
- Physik: Bestimmung von maximalen und minimalen Werten physikalischer Größen.
Mögliche Fragestellungen | Häufig gestellte Fragen (FAQs)
1. Was sind Extremwerte?
Extremwerte sind Punkte, an denen eine Funktion ihre höchsten (Maximum) oder niedrigsten (Minimum) Werte erreicht.
2. Wie findet man Extremwerte?
Durch Berechnung der ersten und zweiten Ableitungen und Überprüfung der Bedingungen für Maxima und Minima.
3. Warum sind Extremwerte wichtig?
Sie helfen, das Verhalten und die Struktur von Funktionen zu verstehen und sind in vielen Bereichen wie Optimierung, Wirtschaft und Physik von Bedeutung.
4. Was ist der Unterschied zwischen lokalen und globalen Extremwerten?
Lokale Extremwerte sind die höchsten oder niedrigsten Werte in einer Umgebung, während globale Extremwerte die höchsten oder niedrigsten Werte im gesamten Definitionsbereich der Funktion sind.
5. Kann eine Funktion mehr als ein Extremwert haben?
Ja, eine Funktion kann mehrere lokale Maxima und Minima haben.
Zusammenfassung
Die Bestimmung von Extremwerten erfordert die Berechnung der ersten und zweiten Ableitungen sowie die Überprüfung der kritischen Punkte.
Diese Methode ist in Mathematik, Wirtschaft und Physik von großer Bedeutung und hilft, das Verhalten und die Struktur von Funktionen präzise zu verstehen.
In der folgenden Lerneinheit zeigen wir dir, wie Ableiten mit der Produktregel abläuft.
Was gibt es noch bei uns?
Optimaler Lernerfolg durch tausende Übungsaufgaben

Quizfrage 1
Quizfrage 2
“Wusstest du, dass unter jedem Kursabschnitt eine Vielzahl von verschiedenen interaktiven Übungsaufgaben bereitsteht, mit denen du deinen aktuellen Wissensstand überprüfen kannst?”
Was ist Technikermathe?
Unser Dozent Jan erklärt es dir in nur 2 Minuten!
Oder direkt den > kostenlosen Probekurs < durchstöbern? – Hier findest du Auszüge aus jedem unserer Kurse!
Geballtes Wissen in derzeit 26 Kursen
Hat dir dieses Thema gefallen? – Ja? – Dann schaue dir auch gleich die anderen Themen zu den Kursen
WT3 (Werkstoffprüfung) und
TM1 (Technische Mechanik – Statik) an.


Perfekte Prüfungsvorbereitung für nur 14,90 EUR/Jahr pro Kurs
++ Günstiger geht’s nicht!! ++
Oder direkt Mitglied werden und Zugriff auf alle 26 Kurse (inkl. Webinare + Unterlagen) sichern ab 7,40 EUR/Monat ++ Besser geht’s nicht!! ++
Social Media? - Sind wir dabei!
Dein Technikermathe.de-Team






