MA3 – Eigenschaften von Exponentialfunktionen [Grundlagen, Beispiele, Tipps]

In dieser Lerneinheit schauen wir uns, die Eigenschaften von Exponentialfunktion an. Eine solche Funktion zeichnet sich dadurch aus, dass der Exponent eine Variable ist und die Basis eine feste Größe. Eine solche Funktion besitzt keine Nullstellen, da sie sich der x-Achse immer weiter annähert, ohne sie jedoch zu schneiden.

Für ein optimales Verständnis helfen dir drei ausführliche Beispiele mit Zahlenwerten zu dem Thema.

Mehr zu diesem Thema und der Mathematik findest du im Kurs: Onlinekurs MA3 – Kurvendiskussion.

Oder lieber mit den Grundlagen starten? Alles dazu findest du im Kurs: Ma1-Grundlagen der Mathematik

Exponentialfunktion | Grundlagen

Was ist eine Exponentialfunktion?

Eine Exponentialfunktion ist eine mathematische Funktion der Form $f(x) = b \cdot a^x$ , wobei $a$ und $b$ Konstanten sind und $b$ eine positive reelle Zahl ungleich 1 ist. Diese Funktion beschreibt viele natürliche Wachstums- und Zerfallsprozesse und ist in der Mathematik, Physik, Biologie, Wirtschaft und vielen anderen Disziplinen von großer Bedeutung.

Exponentialfunktion | Aufbau

Eine Exponentialfunktion weist die folgende Form auf:

Exponentialfunktion

$f(x) = b \cdot a^x$

mit

$a > 0$

$a \neq 1$

$b \neq 0$

Hierbei ist a die Basis. Die Basis a ist eine positive von Null verschiedene reelle Zahl und ungleich 1. Der Faktor b ist eine beliebige von Null verschiedene reelle Zahl.

Bei diesen Funktionen ist der Exponent x die Variable und die Basis a ein fest vorgegebener Wert.

Beispiele für Exponentialfunktionen

Beispiel!

$f(x) = 2^x$ Hier ist b = 1 und a = 2.

$f(x) = 2,3 \cdot 5^x$ Hier ist b = 2,3 und a = 5.

$f(x) = -1,8 \cdot 0,5^x$ Hier ist b = -1,8 und a = 0,5.

Beispiele für keine Exponentialfunktionen

Beispiel!

$f(x) = (-2)^x$ Hier ist b = 1 und a = -0,5.

Die Basis a der Funktion muss positiv und größer als Null sein. In diesem Beispiel ist sie negativ. Für x = 0,5 ist die Funktion beispielsweise nicht definiert:

$(-2)^{0,5} = (-2)^{\frac{1}{2}} = \sqrt{-2}$

Die Wurzel aus einer negativen Zahl ist nicht definiert. Deswegen dürfen diese Funktionen als Basis nur positive reelle Zahlen (außer Null) aufweisen.

Eigenschaften von Exponentialfunktionen

Der Definitionsbereich sind alle reellen Zahlen $\mathbb{R}$ .
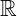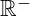Der Wertebereich sind alle positiven reellen Zahlen $\mathbb{R}^+$ , wenn b > 0 ist und alle negativen reellen Zahlen $\mathbb{R}^-$ , wenn b < 0 ist.
Die Funktion schneidet die y-Achse bei dem Faktor b.
Exponentialfunktionen schneiden die x-Achse nicht (keine Nullstellen), sondern haben die x-Achse als Asymptote. Die Funktion nähert sich also der x-Achse immer weiter an, schneidet diese aber nie.

Schauen wir uns dazu mal die folgende Grafik an:

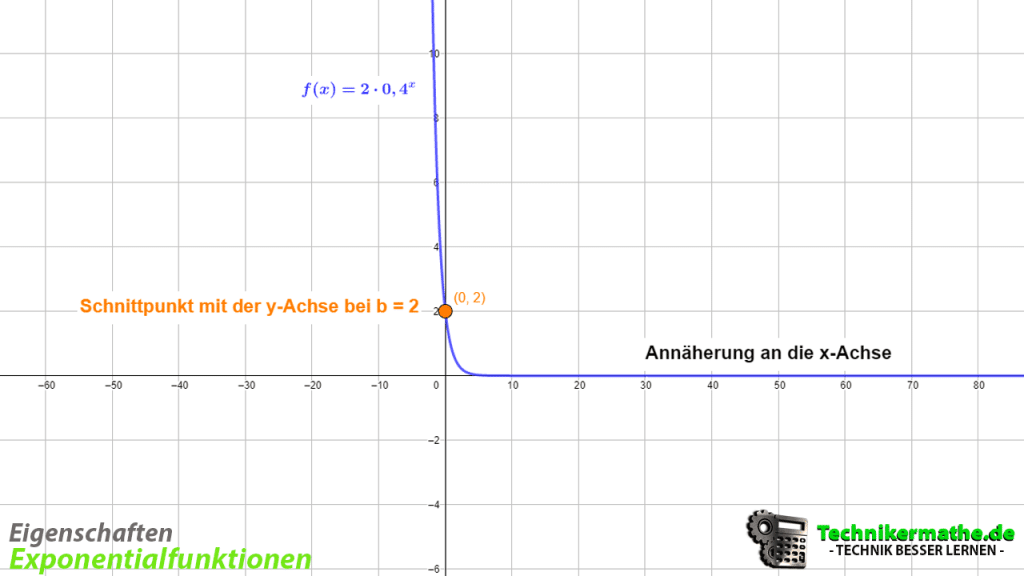
Eigenschaften von Exponentialfunktionen | Schnittpunkt und Annäherung

In der obigen Grafik siehst du die Funktion $f(x) = 2 \cdot 0,4^x$ . Hierbei ist b = 2 und gleichzeitig der Schnittpunkt mit der y-Achse. Alle Exponentialfunktionen haben die x-Achse als Asymptote, d.h. sie nähern sich der x-Achse immer weiter an, jedoch ohne sie zu schneiden. Damit liegen für diese Funktionen auch keine Nullstellen vor. Der Wertebereich der obigen Exponentialfunktion sind alle positiven reellen Zahlen, d.h. der Funktionswert ist für alle x immer positiv. Das können wir auch an dem Faktor b erkennen. Ist dieser größer als Null, so befindet sich die Exponentialfunktion oberhalb der x-Achse.

In der nachfolgenden Grafik betrachten wir eine andere Exponentialfunktion:

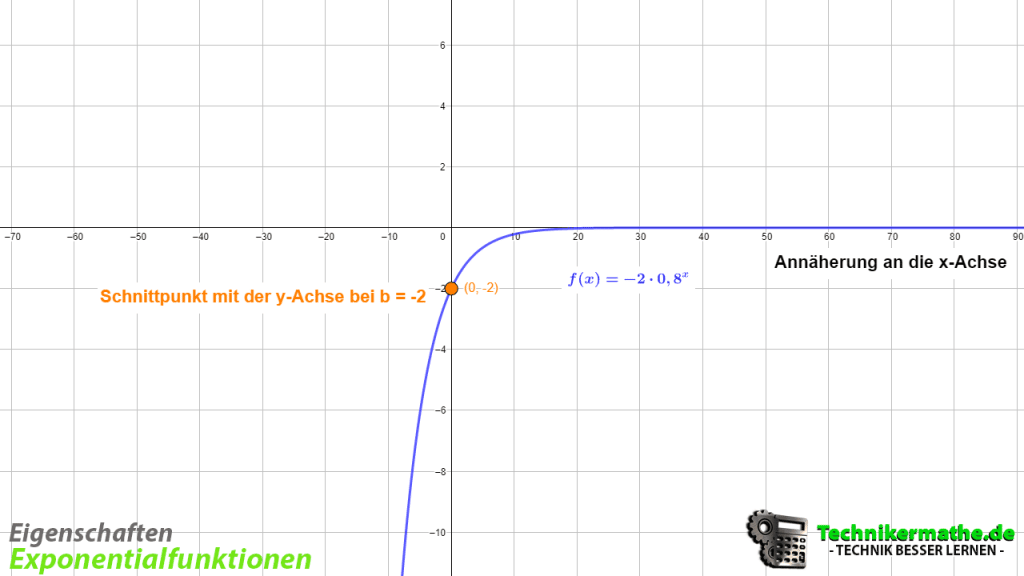
In der obigen Grafik siehst du die Exponentialfunktion $f(x) = -2 \cdot 0,8^x$ . Hierbei ist b = -2 und gleichzeitig der Schnittpunkt mit der y-Achse. Alle Exponentialfunktionen haben die x-Achse als Asymptote, d.h. sie nähern sich der x-Achse immer weiter an, jedoch ohne sie zu schneiden. Damit liegen für Exponentialfunktionen auch keine Nullstellen vor. Der Wertebereich der obigen Exponentialfunktion sind alle negativen reellen Zahlen, d.h. der Funktionswert (y-Wert) ist für alle x immer negativ. Das können wir auch an dem Faktor b erkennen. Ist dieser kleiner als Null, so befindet sich die Exponentialfunktion unterhalb der x-Achse.

Anwendung der Funktionen

Mathematik: Berechnung von Wachstums- und Zerfallsprozessen.
Physik: Analyse von radioaktivem Zerfall und Bevölkerungswachstum.
Biologie: Modellierung von Bakterienwachstum und Medikamentenabbau.
Wirtschaft: Zinseszinsrechnung und Investitionswachstum.

Mögliche Fragestellungen | Häufig gestellte Fragen (FAQs)

1. Was ist eine Exponentialfunktion?

Eine Funktion der Form $f(x) = b \cdot a^x$ , wobei b ein Koeffizient und a eine positive Basis ungleich 1 ist.

2. Wie unterscheidet sich exponentielles Wachstum von exponentiellem Zerfall?

Exponentielles Wachstum tritt auf, wenn $b > 1$ , und exponentieller Zerfall, wenn $0 < b < 1.$

3. Was ist die natürliche Exponentialfunktion?

Die Funktion $f (x) = e^x$ , wobei $e \approx 2.718$ die Eulersche Zahl ist.

4. Wie berechne ich die Ableitung einer Exponentialfunktion?

Die Ableitung von $f(x) = b \cdot a^x$ ist $f'(x) = b \cdot a^x \cdot ln(a)$

5. Welche Anwendungen haben Exponentialfunktionen?

Anwendungen finden sich in der Mathematik, Physik, Biologie und Wirtschaft, insbesondere bei der Modellierung von Wachstums- und Zerfallsprozessen.

Zusammenfassung

Exponentialfunktionen sind zentrale Werkzeuge in der Mathematik und Naturwissenschaften zur Modellierung und Analyse von Prozessen, die Wachstum oder Zerfall beschreiben.

Durch die Identifikation der Basis und des Koeffizienten, die Berechnung von Ableitungen und die graphische Darstellung kann das Verhalten dieser Funktionen umfassend analysiert werden.

Ihre Anwendung reicht von natürlichen Prozessen bis hin zu wirtschaftlichen Modellen, was sie zu einem unverzichtbaren Bestandteil vieler wissenschaftlicher und technischer Disziplinen macht.

Was kommt als Nächstes?

In der folgenden Lerneinheit zeigen wir dir, wie Extremwerte bei gebrochen rationalen Funktionen bestimmt werden.

Was gibt es noch bei uns?

Optimaler Lernerfolg durch tausende Übungsaufgaben

Übungsbereich (Demo) - Lerne mit mehr als 4000 Übungsaufgaben für deine Prüfungen — Übungsbereich (Demo) – Lerne mit mehr als 4000 Übungsaufgaben für deine Prüfungen

Quizfrage 1

Quizfrage 2

“Wusstest du, dass unter jedem Kursabschnitt eine Vielzahl von verschiedenen interaktiven Übungsaufgaben bereitsteht, mit denen du deinen aktuellen Wissensstand überprüfen kannst?”

Alle Technikerschulen im Überblick

Zum Verzeichnis der Technikerschulen (Alles Rund um die Schulen) — Zum Verzeichnis der Technikerschulen

Kennst du eigentlich schon unser großes Technikerschulen-Verzeichnis für alle Bundesländer mit allen wichtigen Informationen (Studiengänge, Kosten, Anschrift, Routenplaner, Social-Media) ? Nein? – Dann schau einfach mal hinein:

Was ist Technikermathe?

Unser Dozent Jan erklärt es dir in nur 2 Minuten!

Oder direkt den > kostenlosen Probekurs < durchstöbern? – Hier findest du Auszüge aus jedem unserer Kurse!

Geballtes Wissen in derzeit 26 Kursen

Hat dir dieses Thema gefallen? – Ja? – Dann schaue dir auch gleich die anderen Themen zu den Kursen

WT3 (Werkstoffprüfung) und
TM1 (Technische Mechanik – Statik) an.

Lerne nun erfolgreich mit unserem Onlinekurs Technische Mechanik 1 — TM1 (Technische Mechanik)

Lerne nun erfolgreich mit unserem Onlinekurs Werkstofftechnik 3 — WT3 (Werkstoffprüfung)

Perfekte Prüfungsvorbereitung für nur 14,90 EUR/Jahr pro Kurs

++ Günstiger geht’s nicht!! ++

Oder direkt Mitglied werden und Zugriff auf alle 26 Kurse (inkl. Webinare + Unterlagen) sichern ab 7,40 EUR/Monat ++ Besser geht’s nicht!! ++