MA3 – e-Funktionen: Verhalten im Unendlichen [Grundlagen, Beispiele, Tipps]

Wir schauen uns in dieser Lerneinheit an, wie das Verhalten einer Funktion im Unendlichen aussieht.

Für ein optimales Verständnis helfen dir drei ausführliche Beispiele mit Zahlenwerten zu dem Thema.

Mehr zu diesem Thema und der Mathematik findest du im Kurs: Onlinekurs MA3 – Kurvendiskussion.

Oder lieber mit den Grundlagen starten? Alles dazu findest du im Kurs: Ma1-Grundlagen der Mathematik

Verhalten im Unendlichen | Grundlagen

Das Verhalten einer Funktion im Unendlichen dient dazu, sich das Aussehen bzw. den Verlauf der Funktion bei sehr großen bzw. sehr kleinen x-Werten vorstellen zu können. Was passiert mit der Funktion z.B. bei einem x-Wert von 1.000.000 oder viel höher bzw. bei einem x-Wert von -1.000.000 oder viel niedriger? Verläuft die Funktion in positive oder negative y-Richtung? Um eine Aussage darüber treffen zu können, untersuchen wir das Verhalten der Funktionswerte (=y-Werte) für positive und negative x-Werte gegen unendlich (∞).

Was ist das Verhalten einer Funktion im Unendlichen?

Das Verhalten einer Funktion im Unendlichen beschreibt, wie sich die Werte einer Funktion $f (x)$ verhalten, wenn $x$ gegen $∞\infty$ oder $−∞-\infty$ geht. Dieses Konzept ist wesentlich in der Analysis, um das langfristige Verhalten von Funktionen zu verstehen und ist besonders wichtig in Bereichen wie Mathematik, Physik und Ingenieurwissenschaften.

Grundprinzipien

Endverhalten: Das Endverhalten einer Funktion gibt an, wie sich 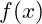$f(x)$ verhält, wenn 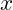$x$ sehr große positive oder negative Werte annimmt.
Asymptoten: Asymptoten sind Linien, denen sich der Graph einer Funktion nähert, aber nicht unbedingt schneidet. Es gibt drei Haupttypen:
- Horizontale Asymptoten: Beschreiben das Verhalten von 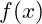$f(x)$ , wenn 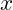$x$ gegen $\pm \infty$ geht.
- Vertikale Asymptoten: Beschreiben das Verhalten von 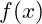$f(x)$ , wenn 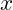$x$ einen bestimmten Wert annähert, bei dem die Funktion nicht definiert ist.
- Schiefe Asymptoten: Beschreiben das Verhalten von 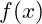$f(x)$ , wenn x gegen $\pm \infty$ geht und die Funktion sich einer schiefen Geraden annähert.

Verhalten im Unendlichen allgemein

Lässt man die x-Werte der Funktion f(x) gegen +∞ oder -∞ laufen, lautet die Schreibweise:

Funktion f(x)

$\lim \limits_{x \to \infty} f(x)$ Verhalten der Funktion bei x gegen plus unendlich

$\lim \limits_{x \to -\infty} f(x)$ Verhalten der Funktion bei x gegen minus unendlich

Aus den vorangegangenen Lektionen wissen wir bereits, wie das Verhalten einer ganzrationalen Funktion n-ten Grades untersucht wird. Wir betrachten in dieser Lektion aber Funktionen, die auch e-Funktionen beinhalten. Deswegen schauen wir uns zunächst einmal an, wie sich die e-Funktion im Unendlichen verhält.

e-Funktion gegen plus unendlich

Wir wollen uns nun anschauen, wie sich die e-Funktion im Unendlichen verhält. Dabei betrachten wir die folgende allgemeine e-Funktion:

Allgemeine e-Funktion

$f(x) = ae^{cx}$

In den folgenden Beispielen wollen wir zunächst schauen, wie sich die e-Funktion der oben angegebenen Form bei x-Werten verhält, die positiv und sehr groß sind. Wir betrachten also das Verhalten bei x gegen plus unendlich. Wir wollen also das Verhalten der Funktion auf der rechten Seite der y-Achse bestimmen.

Schauen wir uns das ganze mal an einem Beispiel an:

Beispiel:

$f(x) = 5e^{2x}$

Untersuche die Funktion für x gegen plus unendlich.

Wir wollen wissen, welchen Wert die Funktionswerte annehmen, wenn x gegen plus unendlich verläuft.

Zunächst einmal zeigen wir, was wir eigentlich vor haben:

$\lim \limits_{x \to \infty} f(x) = \lim \limits_{x \to \infty} 5e^{2x}$

In Worten: Der Limes (=Grenzwert) einer Funktion f(x) für x-Werte gegen +unendlich.

Wir haben die Variable x im Exponenten gegeben. Strebt x gegen plus unendlich, so wird der gesamte Ausdruck e^5x positiv und sehr groß. Damit strebt die Funktion gegen plus unendlich. Wir können uns dazu einfach vorstellen, dass wir eine große Zahl für x einsetzen, z.B. x = 100 (wir können keine größere Zahl einsetzen, weil der Taschenrechner das nicht ausrechnen kann):

$f(x = 100) = 5e^{2 \cdot 100} = 5 \cdot 7,23 \cdot 10^{86} = 3,61 \cdot 10^{87}$

Der Ausdruck 10⁸⁶ besagt, dass wir das Komma um 86 Stellen nach rechts verschieben müssen. Wir erhalten alleine aus e^2·100 eine positive Zahl mit 87 Stellen. Der Faktor 5 vergrößert die Zahl zusätzlich (88 Stellen). Damit strebt die Funktion für x gegen unendlich gegen plus unendlich.

Die Funktion f(x) strebt für x gegen +∞ gegen +∞:

$\lim \limits_{x \to \infty} f(x) = \lim \limits_{x \to \infty} 5e^{2x} = +\infty$

Ist der Faktor vor der e-Funktion nun aber negativ, so ändert sich das Ergebnis. Schauen wir uns dazu ein weiteres Beispiel an:

Beispiel:

$f(x) = -5e^{2x}$

Untersuche die Funktion für x gegen plus unendlich!

Zunächst einmal zeigen wir, was wir eigentlich vor haben:

$\lim \limits_{x \to \infty} f(x) = \lim \limits_{x \to \infty} -5e^{2x}$

In Worten: Der Limes (=Grenzwert) einer Funktion f(x) für x-Werte gegen +unendlich.

In diesem Beispiel ist zwar der Ausdruck e^2x für x gegen unendlich auch positiv und unendlich, durch den negativen Faktor (-5) wird aber aus plus unendlich gleich minus unendlich:

$f(x = 100) = -5e^{2 \cdot 100} = -5 \cdot 7,23 \cdot 10^{86} = -3,61 \cdot 10^{87}$

Wir erhalten alleine aus e^2·100 eine positive Zahl mit 87 Stellen. Der Faktor -5 vergrößert die Zahl und lässt sie negativ werden. Damit strebt die Funktion für x gegen unendlich gegen minus unendlich.

Die Funktion f(x) strebt für x gegen +∞ gegen –∞:

$\lim \limits_{x \to \infty} f(x) = \lim \limits_{x \to \infty} -5e^{2x} = -\infty$

Es kann natürlich ebenfalls vorkommen, dass der Exponent einen negativen Faktor aufweist. Auch hier betrachten wir ein Beispiel:

Beispiel:

$f(x) = 5e^{-2x}$

Untersuche die Funktion für x gegen plus unendlich!

Zunächst einmal zeigen wir, was wir eigentlich vor haben:

$\lim \limits_{x \to \infty} f(x) = \lim \limits_{x \to \infty} 5e^{-2x}$

In Worten: Der Limes (=Grenzwert) einer Funktion f(x) für x-Werte gegen +unendlich.

Wir haben einen negativen Faktor im Exponenten gegeben. Strebt x gegen plus unendlich, so wird der gesamte Ausdruck e^-5x positiv und sehr klein. Ein negativer Exponent bedeutet, dass wir die Potenz auch in den Nenner schreiben können, dann wird der Exponent positiv:

$f(x) = 5e^{-2x} = \frac{5}{e^{2x}}$

Damit strebt die Funktion gegen Null. Denn je größer der Exponent wird, desto kleiner wird der Bruch und dieser strebt immer weiter gegen Null.

Setzen wir wieder x = 100 ein:

$f(x=100) = 5e^{-2x \cdot 100} = 5 \cdot 1,38 \cdot 10^{-87} = 6,91 \cdot 10^{-87} \approx 0$

Die 10^-87gibt an, dass wir das Komma um 87 Stellen nach links verschieben müssen. Damit erhalten wir 0,000….691. Vor den Stellen 691 kommen also insgesamt 84 Nullen. Damit strebt die Funktion gegen Null bei x gegen unendlich.

Die Funktion f(x) strebt für x gegen +∞ gegen 0:

$\lim \limits_{x \to \infty} f(x) = \lim \limits_{x \to \infty} 5e^{-2x} = 0$

e-Funktion gegen minus unendlich

In den folgenden Beispielen wollen wir uns anschauen, wie sich die e-Funktion bei x-Werten verhält, die negativ und sehr groß sind. Wir betrachten also das Verhalten bei x gegen minus unendlich. Wir betrachten hier also das Verhalten der Funktion auf der linken Seite der y-Achse. Die dazugehörigen Grafiken findest du oben.

Schauen wir uns das ganze mal an einem Beispiel an:

Beispiel:

$f(x) = 5e^{2x}$

Untersuche die Funktion für x gegen minus unendlich.

Wir wollen wissen, welchen Wert die Funktionswerte annehmen, wenn x gegen minus unendlich verläuft.

Zunächst einmal zeigen wir, was wir eigentlich vor haben:

$\lim \limits_{x \to -\infty} f(x) = \lim \limits_{x \to -\infty} 5e^{2x}$

In Worten: Der Limes (=Grenzwert) einer Funktion f(x) für x-Werte gegen -unendlich.

Strebt x gegen minus unendlich, so wird der gesamte Ausdruck e^5x positiv und sehr klein. Die Funktion strebt in diesem Fall gegen Null, weil der Exponent negativ wird. Setzen wir dazu x = -100 ein:

$f(x) = 5e^{2 \cdot (-100)} = \frac{5}{e^{2 \cdot 100}} = 5 \cdot 1,38 \cdot 10^{-87} = 6,91 \cdot 10^{-87} \approx 0$

Die Funktion f(x) strebt für x gegen -∞ gegen 0:

$\lim \limits_{x \to -\infty} f(x) = \lim \limits_{x \to -\infty} 5e^{2x} = 0$

Es kann auch sein, dass der Faktor vor der e-Funktion negativ ist. Schauen wir uns dazu ein weiteres Beispiel an:

Beispiel:

$f(x) = -5e^{2x}$

Untersuche die Funktion für x gegen minus unendlich!

Zunächst einmal zeigen wir, was wir eigentlich vor haben:

$\lim \limits_{x \to -\infty} f(x) = \lim \limits_{x \to -\infty} -5e^{2x}$

In Worten: Der Limes (=Grenzwert) einer Funktion f(x) für x-Werte gegen -unendlich.

Strebt x gegen minus unendlich, so wird der gesamte Ausdruck e^5x negativ und sehr klein. Die Funktion strebt in diesem Fall gegen Null, weil der Exponent negativ wird. Setzen wir dazu x = -100 ein:

$f(x) =- 5e^{2 \cdot (-100)} = \frac{-5}{e^{2 \cdot 100}} = -5 \cdot 1,38 \cdot 10^{-87} = -6,91 \cdot 10^{-87} \approx 0$

Wir nähern uns nun von der negativen y-Achse immer weiter der Null an. Das negative Vorzeichen können wir vernachlässigen, denn Null mal -5 ist gleich Null.

Die Funktion f(x) strebt für x gegen -∞ gegen 0:

$\lim \limits_{x \to -\infty} f(x) = \lim \limits_{x \to -\infty} -5e^{2x} = 0$

Es kann natürlich ebenfalls vorkommen, dass der Exponent einen negativen Faktor aufweist. Auch hier betrachten wir ein Beispiel:

Beispiel:

$f(x) = 5e^{-2x}$

Untersuche die Funktion für x gegen minus unendlich!

Zunächst einmal zeigen wir, was wir eigentlich vor haben:

$\lim \limits_{x \to -\infty} f(x) = \lim \limits_{x \to -\infty} 5e^{-2x}$

In Worten: Der Limes (=Grenzwert) einer Funktion f(x) für x-Werte gegen -unendlich.

Strebt x gegen minus unendlich, so wird der gesamte Ausdruck e^-5x positiv und sehr groß. Die Funktion strebt in diesem Fall gegen plus unendlich, weil der Exponent positiv wird. Setzen wir dazu x = -100 ein:

$f(x) = 5e^{-2 \cdot (-100)} = 5e^{2 \cdot 100} = 5 \cdot 7,23 \cdot 10^{86} =3,61 \cdot 10^{87} \approx \infty$

Die Funktion f(x) strebt für x gegen -∞ gegen +∞ :

$\lim \limits_{x \to -\infty} f(x) = \lim \limits_{x \to -\infty} 5e^{-2x} = +\infty$

Merk’s dir!

Wir haben uns nun angeschaut, wie die e-Funktion sich im Unendlichen verhält. Wenn wir eine verschachtelte e-Funktion gegeben haben, so können wir den Satz vom Nullprodukt anwenden, der besagt, dass wir jeden Faktor separat auf das Verhalten im Unendlichen untersuchen können und danach die beiden Ergebnisse überlagern. Was das genau bedeutet, schauen wir uns im nächsten Beispiel an.

Verhalten im Unendlichen bei verschachtelter e-Funktion

Beispiel:

$f(x) = \frac{1}{4} e^{2x} (x^2-2)$

Untersuche die Funktion für x gegen plus und minus unendlich!

Wir haben hier eine verschachtelte e-Funktion gegeben und können den Satz vom Nullprodukt anwenden. Dazu betrachten wir die beiden Faktoren (e-Funktion und quadratische Funktion in der Klammer) separat und untersuchen die beiden Faktoren jeweils auf ihr Verhalten im Unendlichen. Danach überlagern wir beide Ergebnisse.

Faktor 1: e-Funktion

Wir starten mit der e-Funktion und bezeichnen diese Funktion beliebig mit u(x). Wir wollen nun herausfinden, wie sich die e-Funktion für x gegen plus und minus unendlich verhält.

$u(x) = \frac{1}{4} e^{2x}$

Plus unendlich

$\lim \limits_{x \to \infty} u(x) = \lim \limits_{x \to \infty} \frac{1}{4} e^{2x}$

Bei x gegen plus unendlich wird der Exponent positiv. Damit nimmt die e-Funktion e^2x sehr große positive Werte an. Der Faktor vor der e-Funktion (1/4) ist positiv. Damit strebt die Funktion gegen plus unendlich.

Die Funktion u(x) strebt für x gegen +∞ gegen +∞ :

$\lim \limits_{x \to \infty} u(x) = \lim \limits_{x \to \infty} \frac{1}{4} e^{2x} = +\infty$

Minus unendlich

$\lim \limits_{x \to -\infty} u(x) = \lim \limits_{x \to -\infty} \frac{1}{4} e^{2x}$

Bei x gegen minus unendlich wird der Exponent negativ. Damit nimmt die e-Funktion e^2x sehr kleine positive Werte an. Die e-Funktion strebt damit gegen Null. Der Faktor vor der e-Funktion muss damit nicht mehr berücksichtigt werden.

Die Funktion u(x) strebt für x gegen -∞ gegen 0 :

$\lim \limits_{x \to -\infty} u(x) = \lim \limits_{x \to -\infty} \frac{1}{4} e^{2x} = 0$

Faktor 2: Klammer

Wir betrachten als nächstes die Klammer, in welcher sich eine quadratische Funktion befindet. Wie das Verhalten im Unendlichen bei quadratischen Funktionen bzw. Funktionen höherer Ordnung aussieht, kannst du den vorherigen Lektionen dieses Kurses entnehmen.

Wir bezeichnen die Funktion in der Klammer beliebig mit v(x). Wir wollen nun herausfinden, wie sich die Funktion für x gegen plus und minus unendlich verhält.

$v(x) = x^2 -2$

Plus unendlich

$\lim \limits_{x \to \infty} v(x) = \lim \limits_{x \to \infty} x^2 - 2$

Größten Exponenten ausklammern:

$\lim \limits_{x \to \infty} x^2 (1 - \frac{2}{x^2})$

Bei x gegen plus unendlich wird x² positiv und sehr groß (= plus unendlich). Die Klammer nimmt den Wert 1 ein. Der Faktor 1 multipliziert mit plus unendlich führt uns auf plus unendlich. Damit strebt die quadratische Funktion gegen plus unendlich

Die Funktion v(x) strebt für x gegen +∞ gegen +∞:

$\lim \limits_{x \to \infty} v(x) = \lim \limits_{x \to \infty} x^2 -2 = +\infty$

Merk’s dir!

Die Klammer strebt beim Ausklammer des Terms mit größtem Exponenten immer gegen den Konstanten Wert in der Klammer.

Beispiel 2:

Minus unendlich

Zunächst einmal zeigen wir, was wir eigentlich vor haben:

$\lim \limits_{x \to -\infty} v(x) = \lim \limits_{x \to -\infty} x^2 - 2$

Größten Exponenten ausklammern:

$\lim \limits_{x \to -\infty} x^2 (1 - \frac{2}{x^2})$

Bei x gegen minus unendlich wird x² positiv [(-x)² = x²]und sehr groß (= plus unendlich). Die Klammer nimmt den Wert 1 ein. Der Faktor 1 multipliziert mit plus unendlich führt uns auf plus unendlich. Damit strebt die quadratische Funktion gegen plus unendlich

Die Funktion v(x) strebt für x gegen -∞ gegen +∞:

$\lim \limits_{x \to -\infty} f(x) = \lim \limits_{x \to -\infty} x^2 -2 = +\infty$

Überlagerung der Ergebnisse

Im nächsten Schritt schauen wir uns das Verhalten der beiden Funktionen im Unendlichen an und überlagern die Ergebnisse.

Plus unendlich

Faktor 1: u(x) gegen plus unendlich

Faktor 2: v(x) gegen plus unendlich

Damit strebt die Funktion gegen plus unendlich, denn:

$\infty \cdot \infty = \infty$

Die Funktion f(x) strebt für x gegen +∞ gegen +∞ :

$\lim \limits_{x \to \infty} f(x) = \lim \limits_{x \to \infty} \frac{1}{4} e^{2x} (x^2-2) = +\infty$

Minus unendlich

Faktor 1: u(x) gegen Null

Faktor 2: v(x) gegen plus unendlich

Damit strebt die Funktion gegen Null, denn:

$0 \cdot \infty = 0$

Die Funktion f(x) strebt für x gegen -∞ gegen 0:

$\lim \limits_{x \to -\infty} f(x) = \lim \limits_{x \to -\infty} \frac{1}{4} e^{2x} (x^2-2) = 0$

Schauen wir uns die verschachtelte e-Funktion mal in der folgenden Grafik an:

Verhalten im Unendlichen, Verschachtelte Funktion

In der obigen Grafik ist die Funktion eingezeichnet. Wir sehen, dass bei x-Werten gegen +unendlich (positive x-Achse) die Funktionswerte gegen plus unendlich streben. Bei x-Werten gegen minus unendlich (negative x-Achse) hingegen, strebt der Funktionswert gegen Null.

Anwendung des Verhaltens im Unendlichen

Mathematik: Analyse von Funktionsverläufen und Grenzwertbestimmungen.
Physik: Untersuchung von Bewegungen und Kräften in unendlichen Bereichen.
Ingenieurwissenschaften: Simulation von Systemen und Prozessen über lange Zeiträume.
Wirtschaft: Vorhersage von Trends und langfristigem Verhalten wirtschaftlicher Modelle.

Mögliche Fragestellungen | Häufig gestellte Fragen (FAQs)

1. Was ist das Verhalten einer Funktion im Unendlichen?

Es beschreibt, wie sich die Werte einer Funktion $f(x)$ verhalten, wenn $x$ gegen $\infty$ oder $- \infty$ geht.

2. Wie bestimme ich horizontale Asymptoten?

Analysiere die Grenzwerte der Funktion, wenn $x$ gegen $\pm \infty$ geht.

3. Was sind vertikale Asymptoten?

Werte von $x$ , bei denen die Funktion nicht definiert ist und gegen $\pm \infty$ geht.

4. Wann gibt es schiefe Asymptoten?

Wenn keine horizontalen Asymptoten existieren und die Funktion sich einer schiefen Geraden annähert.

5. Wozu dient die Analyse des Verhaltens im Unendlichen?

Zur Vorhersage und Modellierung des langfristigen Verhaltens von Funktionen in verschiedenen wissenschaftlichen und technischen Bereichen.

Zusammenfassung

Das Verhalten einer Funktion im Unendlichen ist entscheidend für das Verständnis und die Analyse von Funktionsverläufen über große Bereiche. Durch die Bestimmung von Asymptoten und das Studium der Grenzwerte liefert diese Analyse wichtige Einblicke in das langfristige Verhalten von Funktionen.

Diese Konzepte sind in vielen wissenschaftlichen und technischen Disziplinen von zentraler Bedeutung und helfen bei der Lösung komplexer Probleme und der Vorhersage von Trends.

Was kommt als Nächstes?

In der folgenden Lerneinheit zeigen wir dir, welche Eigenschaften Exponentialfunktionen besitzen.

Was gibt es noch bei uns?

Optimaler Lernerfolg durch tausende Übungsaufgaben

Übungsbereich (Demo) - Lerne mit mehr als 4000 Übungsaufgaben für deine Prüfungen — Übungsbereich (Demo) – Lerne mit mehr als 4000 Übungsaufgaben für deine Prüfungen

Quizfrage 1

Quizfrage 2

“Wusstest du, dass unter jedem Kursabschnitt eine Vielzahl von verschiedenen interaktiven Übungsaufgaben bereitsteht, mit denen du deinen aktuellen Wissensstand überprüfen kannst?”

Alle Technikerschulen im Überblick

Zum Verzeichnis der Technikerschulen (Alles Rund um die Schulen) — Zum Verzeichnis der Technikerschulen

Kennst du eigentlich schon unser großes Technikerschulen-Verzeichnis für alle Bundesländer mit allen wichtigen Informationen (Studiengänge, Kosten, Anschrift, Routenplaner, Social-Media) ? Nein? – Dann schau einfach mal hinein:

Was ist Technikermathe?

Unser Dozent Jan erklärt es dir in nur 2 Minuten!

Oder direkt den > kostenlosen Probekurs < durchstöbern? – Hier findest du Auszüge aus jedem unserer Kurse!

Geballtes Wissen in derzeit 26 Kursen

Hat dir dieses Thema gefallen? – Ja? – Dann schaue dir auch gleich die anderen Themen zu den Kursen

WT3 (Werkstoffprüfung) und
TM1 (Technische Mechanik – Statik) an.

Lerne nun erfolgreich mit unserem Onlinekurs Technische Mechanik 1 — TM1 (Technische Mechanik)

Lerne nun erfolgreich mit unserem Onlinekurs Werkstofftechnik 3 — WT3 (Werkstoffprüfung)

Perfekte Prüfungsvorbereitung für nur 14,90 EUR/Jahr pro Kurs

++ Günstiger geht’s nicht!! ++

Oder direkt Mitglied werden und Zugriff auf alle 26 Kurse (inkl. Webinare + Unterlagen) sichern ab 7,40 EUR/Monat ++ Besser geht’s nicht!! ++