MA3 – Ableitung mittels Kettenregel

In diesem Kursabschnitt befassen wir und ausführlich mit der Kettenregel. Du erlernst, was die Regel ist, wann du diese anwenden musst und wie die Regel funktioniert.

Für ein optimales Verständnis helfen dir drei ausführliche Beispiele mit Zahlenwerten zu dem Thema.

Mehr zu diesem Thema und der Mathematik findest du im Kurs: Onlinekurs MA3 – Kurvendiskussion.

Oder lieber mit den Grundlagen starten? Alles dazu findest du im Kurs: Ma1-Grundlagen der Mathematik

Kettenregel – Grundlagen | Grundwissen

Die Regel wird gebraucht, wenn eine verschachtelte Funktion, also eine Funktion in einer Funktion, abgeleitet werden soll. Dazu werden die zwei gegebenen Funktionen zu eigenen Teilfunktionen u(x) und v(x). Für diese Teilfunktionen kannst du dann die Ableitungen u'(x) und v'(x) vornehmen. Mit der Regel erhältst du dann aus diesen Angaben die Ableitung f'(x) der gesamten Funktion.

Was ist die Kettenregel?

Die Kettenregel ist eine grundlegende Methode in der Differentialrechnung, die es ermöglicht, die Ableitung einer zusammengesetzten Funktion zu berechnen. Sie ist unverzichtbar für die Analyse von Funktionen, die aus mehreren ineinander geschachtelten Funktionen bestehen.

Grundprinzipien

Zusammengesetzte Funktion:
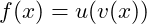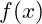Eine zusammengesetzte Funktion ist eine Funktion, die aus zwei oder mehr Funktionen besteht. Zum Beispiel, wenn $f(x) =u(v(x))$ , ist $f(x)$ eine zusammengesetzte Funktion.
Die Kettenregel:
Die Regel besagt, dass die Ableitung einer zusammengesetzten Funktion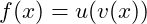 $f(x) = u(v(x))$ durch das Produkt der Ableitungen der äußeren Funktion 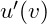$u'(v)$ und der inneren Funktion $u'(x)$ gegeben ist.

Kettenregel | Formel, Funktion

Zunächst betrachtest du die Ausgangsfunktion f(x) mit ihren beiden Funktionen u(x) und v(x):

Ausgangsfunktion

$f(x) = u(v(x))$

BEISPIEL mit linearer Funktion

$f(x) = (4x - 6)^4$

Innerhalb der Klammer haben wir eine lineare Funktion 4x-6 gegeben. Diese Funktion steht nun aber in einer Klammer mit dem Exponenten 4. Wir können hier die Regel anwenden, um die Ableitung der gesamten Funktion zu bestimmen. Wir weisen der inneren linearen Funktion nun einen Funktionsnamen zu, z.B. v(x). Damit ergibt sich dann:

$v(x) = 4x - 6$ Innere Funktion

$u(v) = v^4$ Äußere Funktion

Hierbei ist v bei der äußeren Funktion als Variable zu sehen, so wie x.

Merk’s dir!

Natürlich ist es in diesem Fall auch möglich die Klammer aufzulösen, indem diese geteilt wird (4x-6)² · (4x-6)², dann die 2. Binomische Formel für jede Klammer angewendet wird und danach die beiden resultierenden Klammer miteinander aus multipliziert werden. Da dies aber recht aufwendig ist, können wir auch einfach die Regel anwenden.

Die Regel lautet wie folgt:

Kettenregel

$f'(x) =v'(x) \cdot u'(v)$

BEISPIEL mit Ableitung

Wir betrachten weiterhin das obige Beispiel. u(x) und v(x) haben wir bereits zugeordnet. Als nächstes bilden wir die Ableitungen der beiden Funktionen:

$v(x) = 4x-6 \; \rightarrow \; v'(x) = 4$

$u(v) = v^4 \; \rightarrow \; u'(v) = 4v^3$

Wir können nun die Regel anwenden:

$f'(x) =v'(x) \cdot u'(v)$

Einsetzen der Ableitungen:

$f'(x) = 4 \cdot 4v^3$

Zusammenfassen:

$f'(x) = 16 \cdot v^3$

Einsetzen von v = v(x) = 4x – 6:

$f'(x) = 16 \cdot (4x-6)^3$

Merk’s dir!

Die Regel können wir noch auf viele andere Funktionen anwenden. Wir werden diese später vor allem bei den verschachtelten e-Funktionen und ln-Funktionen zur Bestimmung der Ableitungen benötigen.

Aufgabe 1: Kettenregel mit Wurzel

Wir betrachten jetzt ein paar Aufgaben zur Anwendung der Regel.

Aufgabenstellung

Gegeben sei die folgende Funktion:

$f(x) = \sqrt{2x^2 + 4x - 5}$

Bestimme die Ableitung unter Anwendung der Regel!

Lösung

Wir haben eine Funktion unter eine Wurzel gegeben. Die Ableitung können wir hier mittels Regel vornehmen. Unter der Wurzel haben wir eine quadratische Funktion gegeben:

$v(x) = 2x^2 + 4x - 5$

$u(v) = \sqrt{v}$

Damit ist die äußere Funktion u(x) die Wurzel und die innere Funktion ist die quadratische Funktion v(x) = v. Die Wurzel können wir auch als Potenz darstellen:

$u(v) = v^{\frac{1}{2}}$

Mithilfe dieser Darstellung können wir ganz “normal” ableiten, so wie wir es gewohnt sind:

$f(x) = ax^n \; \rightarrow \; f'(x) = a\cdot n x^{n-1}$

Lösung 2

Wir bilden nun die Ableitungen der beiden Teilfunktionen:

$v'(x) = 4x + 4$

Für die Potenz mit Bruch im Exponenten zeigen wir die Ableitung ausführlich:

$u'(v) = \frac{1}{2} v^{\frac{1}{2} - 1}$

$u'(x) = \frac{1}{2} v^{-\frac{1}{2}}$

Als nächstes wenden wir die Regel an:

$f'(x) = v'(x) \cdot u'(v)$

Einsetzen der Ableitungen:

$f'(x) = (4x+4) \cdot \frac{1}{2} v^{-\frac{1}{2}}$

Einsetzen von v = v(x) = 2x^2 + 4x – 5:

$f'(x) = (4x+4) \cdot \frac{1}{2} (2x^2+4x-5)^{-\frac{1}{2}}$

Wir können den Ausdruck nun wieder als Wurzel darstellen, da der Exponent 1/2 beträgt. Damit haben wir die Quadratwurzel gegeben. Da wir nun aber einen negativen Exponenten gegeben haben, müssen wir die Wurzel in den Nenner setzen (der Exponent wird dann positiv):

$x^{-\frac{1}{2}} = \frac{1}{x^{\frac{1}{2}}} = \frac{1}{\sqrt{x}}$

Mehr Informationen dazu findest du in unserem Onlinekurs MA1 – Vorkurs zur Mathematik.

Wir wenden das Vorgehen auf unser Beispiel an.

Zunächst den Exponenten positiv machen, indem wir einfach die Potenz in den Nenner setzen:

$f'(x) = (4x+4) \cdot \frac{1}{2} \frac{1}{(2x^2+4x-5)^{\frac{1}{2}}}$

Jetzt können wir die Quadratwurzel bilden und ein wenig zusammenfassen:

$f'(x) = (4x+4) \cdot \frac{1}{2} \frac{1}{\sqrt{2x^2+4x-5}}$

$f'(x) = \frac{4x+4}{2\sqrt{2x^2+4x-5}}$

Aufgabe 2: Kettenregel mit Sinus

Aufgabenstellung

Gegeben sei die folgende Funktion:

$f(x) = 5 \cdot sin(x^3)$

Bestimme die Ableitung unter Anwendung der Regel!

Lösung

Wir haben hier innerhalb der Sinusfunktion eine kubische Funktion gegeben. Die Ableitung können wir hier mittels Regel vornehmen:

$v(x) = x^3$ Innere Funktion

$u(v) = sin(v)$ Äußere Funktion

Wir bilden nun die Ableitungen der beiden Teilfunktionen:

$v'(x) = 3x^2$

$u'(v) = cos(v)$

Ableitung der Trigonometrischen Funktionen Sinus und Cosinus im Ableitungskreis:

Ableitungskreis, Cosinus ableiten, sinus ableiten, Trigonometrische Funktionen ableiten, Kettenregel — Ableitungskreis, Cosinus ableiten, Sinus ableiten, Trigonometrische Funktionen ableiten, Kettenregel

Als nächstes wenden wir die Regel an:

$f'(x) = v'(x) \cdot u'(v)$

Einsetzen der Ableitungen:

$f'(x) =3x^2 \cdot cos(v)$

Einsetzen von v = v(x) = x³:

$f'(x) =3x^2 \cdot cos(x^3)$

Anwendung der Kettenregel

Mathematik: Zur Lösung komplexer Ableitungsprobleme.
Physik: Analyse von Bewegungen und Kräften in zusammengesetzten Systemen.
Ingenieurwissenschaften: Modellierung und Simulation von dynamischen Systemen.
Wirtschaft: Optimierung und Analyse von Funktionen mit mehreren Variablen.

Mögliche Fragestellungen | Häufig gestellte Fragen (FAQs)

1. Was ist die Kettenregel?

Die Regel ist eine Methode zur Berechnung der Ableitung einer zusammengesetzten Funktion.

2. Wie funktioniert die Kettenregel?

Die Regel besagt, dass die Ableitung einer zusammengesetzten Funktion das Produkt der Ableitungen der äußeren und inneren Funktionen ist.

3. Wann wird die Kettenregel angewendet?

Die Regel wird angewendet, wenn die zu differenzierende Funktion aus mehreren ineinander geschachtelten Funktionen besteht.

4. Kann die Kettenregel für mehr als zwei Funktionen verwendet werden?

Ja, die Regel kann iterativ auf mehrere ineinander geschachtelte Funktionen angewendet werden.

5. Was sind typische Anwendungsbereiche der Kettenregel?

Typische Anwendungsbereiche sind Mathematik, Physik, Ingenieurwissenschaften und Wirtschaft.

Zusammenfassung

Die Kettenregel ist ein essentielles Werkzeug in der Differentialrechnung zur Berechnung der Ableitung zusammengesetzter Funktionen.

Durch die Identifikation der inneren und äußeren Funktionen und deren Ableitungen ermöglicht die Regel eine systematische und effiziente Bestimmung der gesuchten Ableitung.

Sie ist in vielen Bereichen der Mathematik und angewandten Wissenschaften von großer Bedeutung und wird häufig verwendet, um komplexe Differenzierungsprobleme zu lösen.

Was kommt als Nächstes?

In der folgenden Lerneinheit zeigen wir dir, wie Ableiten mit der Produktregel abläuft.

Was gibt es noch bei uns?

Optimaler Lernerfolg durch tausende Übungsaufgaben

Übungsbereich (Demo) - Lerne mit mehr als 4000 Übungsaufgaben für deine Prüfungen — Übungsbereich (Demo) – Lerne mit mehr als 4000 Übungsaufgaben für deine Prüfungen

Quizfrage 1

Quizfrage 2

“Wusstest du, dass unter jedem Kursabschnitt eine Vielzahl von verschiedenen interaktiven Übungsaufgaben bereitsteht, mit denen du deinen aktuellen Wissensstand überprüfen kannst?”

Alle Technikerschulen im Überblick

Zum Verzeichnis der Technikerschulen (Alles Rund um die Schulen) — Zum Verzeichnis der Technikerschulen

Kennst du eigentlich schon unser großes Technikerschulen-Verzeichnis für alle Bundesländer mit allen wichtigen Informationen (Studiengänge, Kosten, Anschrift, Routenplaner, Social-Media) ? Nein? – Dann schau einfach mal hinein:

Was ist Technikermathe?

Unser Dozent Jan erklärt es dir in nur 2 Minuten!

Oder direkt den > kostenlosen Probekurs < durchstöbern? – Hier findest du Auszüge aus jedem unserer Kurse!

Geballtes Wissen in derzeit 26 Kursen

Hat dir dieses Thema gefallen? – Ja? – Dann schaue dir auch gleich die anderen Themen zu den Kursen

WT3 (Werkstoffprüfung) und
TM1 (Technische Mechanik – Statik) an.

Lerne nun erfolgreich mit unserem Onlinekurs Technische Mechanik 1 — TM1 (Technische Mechanik)

Lerne nun erfolgreich mit unserem Onlinekurs Werkstofftechnik 3 — WT3 (Werkstoffprüfung)

Perfekte Prüfungsvorbereitung für nur 14,90 EUR/Jahr pro Kurs

++ Günstiger geht’s nicht!! ++

Oder direkt Mitglied werden und Zugriff auf alle 26 Kurse (inkl. Webinare + Unterlagen) sichern ab 7,40 EUR/Monat ++ Besser geht’s nicht!! ++