MA2 – Cramersche Regel – Determinantenverfahren

In dieser Lerneinheit betrachten wir die Cramersche Regel zur Lösung von linearen Gleichungssystemen mit mehr als zwei unbekannten Variablen.

Für ein optimales Verständnis helfen dir zwei Videoclips und mehrere ausführliche Beispiele mit Zahlenwerten zu dem Thema.

Mehr zu diesem Thema und der Mathematik findest du im Kurs: Ma2-Lineare Gleichungssysteme:

Oder lieber mit den Grundlagen starten? Alles dazu findest du im Kurs: Ma1-Grundlagen der Mathematik

Cramersche Regel | Grundlagen

Cramersche Regel - Lösen von Gleichungssystemen — Cramersche Regel – Lösen von Gleichungssystemen

Was ist die Cramersche Regel?

Die Cramersche Regel ist eine Methode zur Lösung linearer Gleichungssysteme, die Determinanten verwendet. Sie ist besonders nützlich für Systeme, die genauso viele Gleichungen wie Unbekannte haben und eine eindeutige Lösung besitzen.

Die Regel ist nach dem Schweizer Mathematiker Gabriel Cramer benannt, der das Verfahren in der ersten Hälfte des 18. Jahrhundert entwickelt hat. Das Verfahren kann auf ein Gleichungssystem angewendet werden, welches genau so viele Gleichungen wie unbekannte Variablen aufweist. Man spricht dann von einem quadratischen linearen Gleichungssystem.

Damit du das Verfahren vollständig verstehst, schauen wir uns den Ablauf anhand eines ausführlichen Beispiels an.

Cramersche Regel: Ablauf

Gegeben sei das folgende lineare Gleichungssystem:

(1) $x_1 - x_2 + 2x_3 = 6$

(2) $2x_1 + 3x_2 + 2x_3 = 11$

(3) $3x_1 + 2x_2 + x_3 = 8$

Schritt 1: Koeffizientenmatrix aufstellen

Im ersten Schritt übertragen wir nun die Koeffizienten in eine Matrix, die sogenannte Koeffizientenmatrix (die Ergebnisspalte wird nicht mit übertragen):

$\begin{huge}\begin{vmatrix} 1 & -1 & 2 \\2 & 3 & 2 \\ 3 & 2 & 1 \end{vmatrix} \end{huge}$

Schritt 2: Determinante berechnen (Regel von Sarrus)

Wir berechnen als nächstes die Determinante der obigen Koeffizientenmatrix. Bei einer gegebenen 3X3-Matrix können wir dazu die Regel von Sarrus anwenden:

Die Vorgehensweise nach der Regel von Sarrus ist im obigen Bild erläutert. In der folgenden Box findest du diese nochmals verfasst.

Vorgehensweise: Regel von Sarrus

Zunächst fügst du die ersten beiden Spalten hinten an die gegebene Matrix an.
Danach bildest du Diagonalen. Zunächst die Diagonalen die von oben links nach unten rechts verlaufen (dabei startest du beim ersten Koeffizienten). Es müssen immer drei Koeffizienten auf einer Diagonalen liegen.
Danach bildest du die Diagonalen ausgehend vom ersten Koeffizienten der letzten Zeile von unten links nach oben rechts.
Die Koeffizienten auf den Diagonalen werden dann miteinander multipliziert und das Ergebnis entweder addiert (siehe Determinanten von links oben nach rechts unten) oder subtrahiert (siehe Determinanten von links unten nach rechts oben).
Am Ende erhältst du die Determinante.

Für unser Beispiel erhältst du also als Determinante der Koeffizientenmatrix:

$D = \begin{huge}\begin{vmatrix} 1 & -1 & 2 \\2 & 3 & 2 \\ 3 & 2 & 1 \end{vmatrix} \end{huge} = -15$

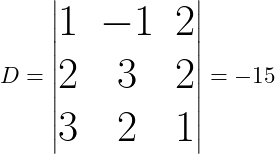
Schritt 3: Hilfsdeterminanten berechnen (Regel von Sarrus)

Wir starten nun damit die Ergebnisspalte (siehe rechte Seite vom Gleichheitszeichens des linearen Gleichungssystems) zu verwenden und Hilfsdeterminanten zu berechnen.

Wir fügen dazu die Ergebnisspalte zunächst in die erste Spalte ein, danach in die zweite Spalte und zum Schluss in die dritte Spalte. Wir erhalten somit drei Matrizen, für welche wir jeweils die Determinanten berechnen müssen:

Cramersche Regel, Hilfsdeterminanten — Regel, Hilfsdeterminanten

Wir ersetzen somit die gegebenen Spalten durch die Ergebnisspalte und berechnen dann im nächsten Schritt die Determinanten mittels Regel von Sarrus:

Cramersche Regel | Berechnung — Berechnung

Nachdem du die Hilfsdeterminanten bestimmt hast, kannst du als nächstes damit beginnen, die unbekannten Variablen zu berechnen.

Schritt 4: Unbekannte Variablen berechnen

Zur Bestimmung der unbekannten Variablen berechnest du die folgenden Quotienten:

$x_1 = \dfrac{D_{x_1}}{D}$ x₁ berechnen

$x_2 = \dfrac{D_{x_2}}{D}$ x₂ berechnen

$x_3 = \dfrac{D_{x_3}}{D}$ x₃ berechnen

Einsetzen der berechneten Determinanten:

$x_1 = \dfrac{-15}{-15} = 1$

$x_2 = \dfrac{-15}{-15} = 1$

$x_3 = \dfrac{-45}{-15} = 3$

Die Lösung des linearen Gleichungssystem ist also:

$L = \{x_1, x_2, x_3 \} = \{1, 1, 3 \}$

Der Gauß Algorithmus (vorangegangene Lerneinheit) und die Regel von Cramer führen zum selben Ergebnis. Da innerhalb der Praxis häufig nicht allzu große Gleichungssysteme vorkommen, ist die Regel schneller durchführbar, als der Gauß Algorithmus. Außerdem kann die Regel nach Cramer programmiert werden, so dass sich auch umfangreiche Gleichungssysteme berechnen lassen.

Anwendung der Regel von Cramer

Mathematik: Lösung von linearen Gleichungssystemen.
Ingenieurwissenschaften: Analyse von Netzwerken und mechanischen Systemen.
Wirtschaft: Optimierung und Analyse von Modellen mit linearen Gleichungen.

Mögliche Fragestellungen | Häufig gestellte Fragen (FAQs)

1. Was ist die Cramersche Regel?

Die Regel ist eine Methode zur Lösung von linearen Gleichungssystemen durch Verwendung von Determinanten.

2. Wie funktioniert die Regel?

Die Regel berechnet die Lösung eines Gleichungssystems, indem sie die Determinanten der Koeffizientenmatrix und modifizierter Matrizen verwendet, bei denen einzelne Spalten durch den Vektor der Konstanten ersetzt werden.

3. Wann wird die Regel angewendet?

Die Regel wird angewendet, wenn ein lineares Gleichungssystem mit genauso vielen Gleichungen wie Unbekannten vorliegt und die Koeffizientenmatrix eine nicht-null Determinante hat.

4. Kann die Cramersche Regel für große Systeme verwendet werden?

Die Anwendung der Regel für große Systeme ist theoretisch möglich, aber oft ineffizient wegen des hohen Rechenaufwands bei der Berechnung von Determinanten großer Matrizen.

5. Was ist der Unterschied zwischen der Regel und anderen Lösungsmethoden?

Die Regel verwendet Determinanten, während andere Methoden wie der Gauß-Algorithmus oder Iterationsverfahren auf Zeilenoperationen oder wiederholten Näherungen basieren.

Zusammenfassung

Die Regel ist ein effektives Verfahren zur Lösung linearer Gleichungssysteme mit Determinanten.

Durch das Ersetzen der Spalten der Koeffizientenmatrix mit dem Konstantenvektor und die Berechnung der entsprechenden Determinanten, bietet diese Methode eine direkte Lösung für Systeme mit genauso vielen Gleichungen wie Unbekannten.

Die Regel findet breite Anwendung in Mathematik, Ingenieurwissenschaften und Wirtschaft, obwohl sie für sehr große Systeme ineffizient sein kann.

Was kommt als Nächstes?

In der folgenden Lerneinheit findest du eine ausführliche Formelsammlung zu diesem Onlinekurs.

Was gibt es noch bei uns?

Optimaler Lernerfolg durch tausende Übungsaufgaben

Übungsbereich (Demo) - Lerne mit mehr als 4000 Übungsaufgaben für deine Prüfungen — Übungsbereich (Demo) – Lerne mit mehr als 4000 Übungsaufgaben für deine Prüfungen

Quizfrage 1

Quizfrage 2

“Wusstest du, dass unter jedem Kursabschnitt eine Vielzahl von verschiedenen interaktiven Übungsaufgaben bereitsteht, mit denen du deinen aktuellen Wissensstand überprüfen kannst?”

Alle Technikerschulen im Überblick

Zum Verzeichnis der Technikerschulen (Alles Rund um die Schulen) — Zum Verzeichnis der Technikerschulen

Kennst du eigentlich schon unser großes Technikerschulen-Verzeichnis für alle Bundesländer mit allen wichtigen Informationen (Studiengänge, Kosten, Anschrift, Routenplaner, Social-Media) ? Nein? – Dann schau einfach mal hinein:

Was ist Technikermathe?

Unser Dozent Jan erklärt es dir in nur 2 Minuten!

Oder direkt den > kostenlosen Probekurs < durchstöbern? – Hier findest du Auszüge aus jedem unserer Kurse!

Geballtes Wissen in derzeit 26 Kursen

Hat dir dieses Thema gefallen? – Ja? – Dann schaue dir auch gleich die anderen Themen zu den Kursen

WT3 (Werkstoffprüfung) und
TM1 (Technische Mechanik – Statik) an.

Lerne nun erfolgreich mit unserem Onlinekurs Technische Mechanik 1 — TM1 (Technische Mechanik)

Lerne nun erfolgreich mit unserem Onlinekurs Werkstofftechnik 3 — WT3 (Werkstoffprüfung)

Perfekte Prüfungsvorbereitung für nur 14,90 EUR/Jahr pro Kurs

++ Günstiger geht’s nicht!! ++

Oder direkt Mitglied werden und Zugriff auf alle 26 Kurse (inkl. Webinare + Unterlagen) sichern ab 7,40 EUR/Monat ++ Besser geht’s nicht!! ++