MA2 – Additionsverfahren | Subtraktionsverfahren [Grundlagen, Erklärung, Videoclips, Aufgaben & Tipps]

In dieser Lerneinheit wollen wir uns anschauen, wie du lineare Gleichungssysteme mit zwei Unbekannten mittels Additionsverfahren und Subtraktionsverfahren lösen kannst.

Für ein optimales Verständnis helfen dir zwei Videoclips und mehrere ausführliche Beispiele mit Zahlenwerten zu dem Thema.

Mehr zu diesem Thema und der Mathematik findest du im Kurs: Ma2-Lineare Gleichungssysteme:

Oder lieber mit den Grundlagen starten? Alles dazu findest du im Kurs: Ma1-Grundlagen der Mathematik

Lernclips | Additionsverfahren

In den folgenden beiden Videos zeigen wir euch, wie das Additionsverfahren funktioniert.

Lernclips | Additionsverfahren

Additionsverfahren | Subtraktionsverfahren | Grundlagen

Additionsverfahren und Subtraktionsverfahren | Grundlagen

Das Additionsverfahren und das Subtraktionsverfahren sind Methoden zum Lösen von linearen Gleichungssystemen.

Was sind das Additionsverfahren und das Subtraktionsverfahren?

Das Additionsverfahren und das Subtraktionsverfahren sind Techniken zur Lösung von linearen Gleichungssystemen. Diese Methoden zielen darauf ab, eine der Variablen zu eliminieren, um das System zu vereinfachen und die Lösung zu finden.

Schritte zur Anwendung des Additionsverfahrens

Gleichungen aufstellen: Identifiziere die beiden Gleichungen des Systems. Zum Beispiel:

$\begin{cases} 2x + 3y = 11 \\ 4x - 3y = 1 \end{cases}$
Gleichungen addieren: Addiere die beiden Gleichungen, um eine Variable zu eliminieren. Hier werden die y-Terme eliminiert:

$(2x + 3y) + (4x - 3y) = 11 + 1$
$6x = 12$
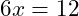
Lösung für eine Variable finden: Löse die resultierende Gleichung nach der verbleibenden Variablen auf:

$x = \frac{12}{6} = 2$
Zweite Variable berechnen: Setze den Wert der gelösten Variablen in eine der ursprünglichen Gleichungen ein, um die andere Variable zu finden:
$2(2) + 3y = 11$

Schritte zur Anwendung des Subtraktionsverfahrens

Gleichungen aufstellen: Identifiziere die beiden Gleichungen des Systems. Zum Beispiel:
$\begin{cases} 5x + 4y = 20 \\ 3x + 4y = 12 \end{cases}$
Gleichungen subtrahieren: Subtrahiere die zweite Gleichung von der ersten, um eine Variable zu eliminieren:
$(5x + 4y) − (3x + 4y) =20−12$
Lösung für eine Variable finden: Löse die resultierende Gleichung nach der verbleibenden Variablen auf:

$x = \frac{8}{2} = 4$
Zweite Variable berechnen: Setze den Wert der gelösten Variablen in eine der ursprünglichen Gleichungen ein, um die andere Variable zu finden:

$3(4) + 4y = 12$
$12 + 4y = 12$
$4y = 0$
$y = 0$

Bei den Verfahren werden die Gleichungen in einem Gleichungssystem entweder miteinander addiert oder voneinander subtrahiert, je nachdem, was zur gewünschten Lösung führt.

Ziel ist es durch die Addition bzw. Subtraktion eine der unbekannten Variablen (x oder y) zu eliminieren, damit letztlich nur noch eine Gleichung mit einer Variablen übrig bleibt. Diese Gleichung kann dann nach der verbleibenden Variablen aufgelöst werden.

Beispiel: Additionsverfahren

Damit du das Verfahren nachvollziehen kannst, schauen wir uns zunächst ein ganz einfaches Beispiel an:

Beispiel!

Gleichungssystem

I. 2x + 4y = 5

II. -2x + 2y = 7

Der erste Schritt den du beim Additionsverfahren durchführen musst, ist zu entscheiden, welche Unbekannte (also entweder x oder y) du eliminieren möchtest. Eliminieren bedeutet, dass diese Unbekannte wegfällt.

Dein Ziel ist es beide Gleichungen miteinander zu addieren. Dabei kannst du einfach die Terme die untereinander stehen miteinander addieren. Du siehst, dass die Gleichung I: 2x und Gleichung II: -2x aufweisen. Wenn du nun beide Terme miteinander addierst, dann erhältst du:

+ -2x

= 0

Die Variable x würde also wegfallen, wenn wir die beiden Gleichungen miteinander addieren. Natürlich müssen wir die Addition für die gesamte Gleichung durchführen:

2x + 4y = 5

+ -2x + 2y = 7

_____________

0 + 6y = 12

6y = 12

Wir haben es nun also geschafft, dass eine Unbekannte wegfällt. Wir können die resultierende Gleichung nun nach y auflösen:

6y = 12 |:6

y = 2

Als nächstes setzt du y = 2 in eine der obigen Ausgangsgleichungen ein:

I. 2x + 4 · 2 = 5

2x + 8 = 5 |-8

2x = -3 |:2

x = -1,5

Du hast nun beide Unbekannten mittels Additionsverfahren gelöst.

Beispiel: Subtraktionsverfahren

Beispiel!

Das Subtraktionsverfahren ist nichts anderes, nur dass beide Gleichungen voneinander subtrahiert werden. Schauen wir uns dazu mal ein weiteres Beispiel an:

I. -5x + 3y = 20

II. 7x + 3y = 14

Du siehst, dass 3y in beiden Gleichungen vorkommt. Wenn du nun die II. von der I. subtrahierst, dann fällt dieser Term weg und damit die unbekannte Variable y:

-5x + 3y = 20

–(7x + 3y = 14)

Du ziehst nun also die Terme untereinander ab:

-5x + 3y = 20

–7x – 3y = -14

____________

-12x + 0 = 6

-12x = 6

Als nächstes löst du nach x auf:

-12x = 6 |:(-12)

x = -0,5

Danach setzt du x = -0,5 in eine der beiden obigen Gleichungen ein und löst nach y auf:

I. -5 · (-0,5) + 3y = 20

2,5 + 3y = 20 |-2,5

3y = 17,5 |:3

y = 5,83

Additionsverfahren / Subtraktionsverfahren mit Umformungen

Natürlich kann es auch vorkommen, dass du zunächst Gleichungen umformen musst, bevor du das Additionsverfahren / Subtraktionsverfahren anwenden kannst. Schauen wir uns dazu das folgende Beispiel an:

I. 3x – y = 7

II. -x + 2y = -1

Bei diesem Gleichungssystem kannst du die beiden Gleichungen nicht sofort miteinander addieren oder voneinander subtrahieren. Hier musst du zunächst eine Gleichung umformen, damit du weiter rechnen kannst. Überlege dir zunächst welche Variable du eliminieren möchtest.

Willst du x entfernen, dann könntest du die II. Gleichung mit 3 multiplizieren und dann die Addition durchführen:

I. 3x – y = 7

II. -x + 2y = -1 |·3

Das ergibt:

I. 3x – y = 7

II. -3x + 6y = -3

Du kannst nun beide Gleichungen miteinander addieren, damit fällt die Variable x weg:

3x – y = 7

+ -3x + 6y = -3

___________

0 + 5y = 4

5y = 4

Auflösen nach y:

5y = 4 |:5

y =0,8

Einsetzen in die Gleichung I:

I. 3x – 0,8 = 7 |+0,8

3x + = 7,8 |:3

x = 2,6

Sollst du das Additionsverfahren bzw. Subtraktionsverfahren zur Berechnung linearer Gleichungssysteme mit zwei Unbekannten durchführen, dann hilft dir die folgende Vorgehensweise:

Merk’s dir!

1.Entscheide, welche Unbekannte du eliminieren willst.

2. Überlege welche Umformungen du ggfs. durchführen musst

3. Addiere oder subtrahiere die Gleichungen, so dass eine Unbekannte wegfällt.

4. Lösen nach der verbleibenden Unbekannten auf.

5. Berechne die andere Unbekannte, indem du die verbleibende Unbekannte in eine der Gleichungen einsetzt.

Lineare Gleichungssysteme mit zwei Unbekannten kannst du also mittels Gleichsetzungsverfahren (vorige Lerneinheit), Additions- bzw. Subtraktionsverfahren sowie dem Einsetzungsverfahren (folgende Lerneinheit)lösen. Sollte nicht explizit angegeben sein, welches Verfahren du verwenden sollst, kannst du dir eines der Verfahren aussuchen.

Anwendung der Additions- und Subtraktionsverfahren

Mathematik: Lösung von linearen Gleichungssystemen.
Physik: Berechnung von unbekannten Größen in Gleichungssystemen.
Ingenieurwesen: Analyse von Systemen mit mehreren Variablen.

Mögliche Fragestellungen | Häufig gestellte Fragen (FAQs)

1. Was ist das Additionsverfahren?

Eine Methode zur Lösung von Gleichungssystemen durch Addition der Gleichungen, um eine Variable zu eliminieren.

2. Was ist das Subtraktionsverfahren?

Eine Methode zur Lösung von Gleichungssystemen durch Subtraktion der Gleichungen, um eine Variable zu eliminieren.

3. Wann verwendet man das Additionsverfahren?

Wenn die Koeffizienten einer Variablen in den Gleichungen entgegengesetzte Vorzeichen haben.

4. Wann verwendet man das Subtraktionsverfahren?

Wenn die Koeffizienten einer Variablen in den Gleichungen gleich sind.

5. Warum sind diese Verfahren wichtig?

Sie sind grundlegende Methoden zur Lösung von Gleichungssystemen, die in vielen wissenschaftlichen und technischen Bereichen verwendet werden.

Zusammenfassung

Das Additionsverfahren und das Subtraktionsverfahren sind grundlegende Techniken zur Lösung von linearen Gleichungssystemen.

Das Additionsverfahren eliminiert eine Variable durch Addition der Gleichungen, während das Subtraktionsverfahren dies durch Subtraktion erreicht.

Beide Verfahren sind wichtige Werkzeuge in Mathematik, Physik und Ingenieurwesen und helfen, Systeme mit mehreren Variablen effizient zu lösen.

Was kommt als Nächstes?

In der folgenden Lerneinheit zeigen wir dir, wie das Einsetzungsverfahren funktioniert.

Was gibt es noch bei uns?

Optimaler Lernerfolg durch tausende Übungsaufgaben

Übungsbereich (Demo) - Lerne mit mehr als 4000 Übungsaufgaben für deine Prüfungen — Übungsbereich (Demo) – Lerne mit mehr als 4000 Übungsaufgaben für deine Prüfungen

Quizfrage 1

Quizfrage 2

“Wusstest du, dass unter jedem Kursabschnitt eine Vielzahl von verschiedenen interaktiven Übungsaufgaben bereitsteht, mit denen du deinen aktuellen Wissensstand überprüfen kannst?”

Alle Technikerschulen im Überblick

Zum Verzeichnis der Technikerschulen (Alles Rund um die Schulen) — Zum Verzeichnis der Technikerschulen

Kennst du eigentlich schon unser großes Technikerschulen-Verzeichnis für alle Bundesländer mit allen wichtigen Informationen (Studiengänge, Kosten, Anschrift, Routenplaner, Social-Media) ? Nein? – Dann schau einfach mal hinein:

Was ist Technikermathe?

Unser Dozent Jan erklärt es dir in nur 2 Minuten!

Oder direkt den > kostenlosen Probekurs < durchstöbern? – Hier findest du Auszüge aus jedem unserer Kurse!

Geballtes Wissen in derzeit 26 Kursen

Hat dir dieses Thema gefallen? – Ja? – Dann schaue dir auch gleich die anderen Themen zu den Kursen

WT3 (Werkstoffprüfung) und
TM1 (Technische Mechanik – Statik) an.

Lerne nun erfolgreich mit unserem Onlinekurs Technische Mechanik 1 — TM1 (Technische Mechanik)

Lerne nun erfolgreich mit unserem Onlinekurs Werkstofftechnik 3 — WT3 (Werkstoffprüfung)

Perfekte Prüfungsvorbereitung für nur 14,90 EUR/Jahr pro Kurs

++ Günstiger geht’s nicht!! ++

Oder direkt Mitglied werden und Zugriff auf alle 26 Kurse (inkl. Webinare + Unterlagen) sichern ab 7,40 EUR/Monat ++ Besser geht’s nicht!! ++