Wir schauen uns in dieser Lerneinheit an, wie du für eine lineare Funktion grafisch und rechnerisch die Nullstelle bestimmen kannst.
Für ein optimales Verständnis helfen dir zwei Videoclips und mehrere ausführliche Beispiele mit Zahlenwerten zu dem Thema. Mehr zu diesem Thema und der Mathematik findest du im Kurs: Ma2-Lineare Gleichungssysteme: Oder lieber mit den Grundlagen starten? Alles dazu findest du im Kurs: Ma1-Grundlagen der Mathematik
Nullstellen linearer Funktionen | Grundlagen
Was sind Nullstellen linearer Funktionen?
Die Nullstellen einer linearen Funktion sind die x-Werte, bei denen der Funktionswert y gleich null ist. Diese Nullstellen geben an, wo die Gerade die x-Achse schneidet.
“Nullstellen von Funktionen sind ganz allgemein die Schnittpunkte der gegebenen Funktion mit der x-Achse, also mit der Abzisse.”
Wir wollen uns mal anschauen, wie die Nullstellen grafisch und rechnerisch bestimmt werden können. Schauen wir uns dazu die folgende lineare Funktion an:
Die obige lineare Funktion schneidet die x-Achse bei 
und bei 
. Willst du den Schnittpunkt als Punkt angeben so gilt:
S(3/0)
Hierbei gilt, dass die y-Koordinate des Schnittpunktes der Funktion mit der x-Achse immer Null ist. Es reicht demnach aus, die x-Koordinaten anzugeben. Diese x-Koordinaten wird auch als Nullstelle bezeichnet. Damit ist klar, dass es sich hierbei um den Schnittpunkt der Funktion mit der x-Achse handelt.
Nullstelle bestimmen –
Bei einer linearen Funktion gibt es nur eine Nullstelle, demnach also nur einen Schnittpunkt mit der x-Achse. Diesen Wert kannst du – wie oben gezeigt – entweder grafisch bestimmen, indem du die Funktion einzeichnest und die Nullstelle abliest oder du bestimmst die Nullstelle rechnerisch.
Die zweite Variante ist häufig die bevorzugte, weil sie sehr schnell geht und der berechnete Wert exakt bestimmt werden kann. Bei der grafischen Variante kann es passieren, dass die Nullstelle nicht exakt abgelesen wird, wenn der Maßstab ungünstig gewählt oder die Funktion nicht genau eingezeichnet wurde.
Die Nullstellen von Funktionen werden allgemein wie folgt berechnet:
- Zunächst setzt du die Funktion gleich Null:
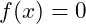
- Danach löst du die Funktion nach
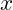auf.
Du setzt also die Funktion zunächst gleich Null. Das machst du, weil du den x-Wert berechnen möchtest, bei welchem der y-Wert gleich Null ist:
Das ist nämlich genau der Schnittpunkt mit der x-Achse, also die gesuchte Nullstelle. Um den x-Wert zu bestimmen, musst du dann die Funktion nach x auflösen. Das kennst du bereits aus den Lerneinheiten Lösen linearer Gleichungen.
Wir schauen uns dazu ein Beispiel an.
Beispiel | Nullstelle bestimmen
Gegeben sei die folgende Funktion:
Von dieser Funktion die Nullstelle bestimmen!
1.Zunächst setzt du die Funktion gleich Null:
2.Danach löst du die Funktion nach auf:
|
|
Die Nullstelle der Funktion ist bei gegeben. An dieser Stelle schneidet die Funktion die x-Achse. Der y-Wert ist an dieser Stelle Null.
Bei linearen Funktionen gibt es genau eine Nullstelle, demnach einen Schnittpunkt mit der x-Achse.
Die Nullstelle kann grafisch ermittelt werden, indem der Graph eingezeichnet und die Nullstelle (Schnittpunkt mit der x-Achse) abgelesen wird.
Die Nullstelle kann auch rechnerisch ermittelt werden, indem die Funktion gleich Null gesetzt und nach aufgelöst wird.
Lernclip | Nullstelle bestimmen bei linearer Funktion
Im folgenden Video zeige ich dir, wie du die Nullstelle einer Funktion grafisch und rechnerisch ermittelst:
Schauen wir uns dazu mal einige Beispiele an.
Aufgaben| Nullstelle berechnen
In den folgenden beiden Aufgaben lernst du, wie die Nullstellen für lineare Funktionen bestimmt werden.
Aufgabe 1 | Nullstelle bestimmen
Gegeben sei die folgende lineare Funktionsgleichung:
An welcher Stelle schneidet die Funktion die x-Achse?
Wir wollen hier den Schnittpunkt der Funktion mit der x-Achse bestimmen. Hierbei handelt es sich um die Nullstelle der Funktion. Um diese zu berechnen, müssen wir zunächst die Funktion gleich Null setzen:
Danach lösen wir die obige Funktion nach auf. Ziel ist es nun, dass auf einer Seite alleine steht:
|
|
An der Stelle bzw. im Punkt (4|0) schneidet die Funktion die x-Achse. Hier ist also eine Nullstelle gegeben.
Aufgabe 2 : Nullstelle bestimmen
Gegeben sei die folgende lineare Funktion:
Von dieser Funktion die Nullstelle bestimmen!
Auch hier geht es wieder darum die Nullstelle der Funktion und damit den Schnittpunkt mit der x-Achse zu bestimmen. Der erste Schritt ist wieder die Funktion gleich Null zu setzen, weil für die Nullstelle der y-Wert zu Null wird:
also
Danach lösen wir die obige Gleichung nach auf:
|
|
An der Stelle bzw. im Punkt (15|0) ist die Nullstelle der Funktion gegeben. Hier schneidet die Funktion die x-Achse.
Anwendung der Nullstellen
- Mathematik: Analyse und Darstellung von Geraden und ihren Schnittpunkten mit der x-Achse.
- Physik: Berechnung von Momenten, in denen eine physikalische Größe null ist.
- Wirtschaft: Bestimmung von Gewinn- oder Verlustpunkten.
Mögliche Fragestellungen | Häufig gestellte Fragen (FAQs)
1. Was sind Nullstellen linearer Funktionen?
Nullstellen sind die x-Werte, bei denen der Funktionswert y gleich null ist. Sie zeigen an, wo die Gerade die x-Achse schneidet.
2. Wie findet man die Nullstellen?
Setze die Funktionsgleichung gleich null und löse die Gleichung nach x auf.
3. Was bedeutet eine Nullstelle für die Grafik der Funktion?
Eine Nullstelle zeigt den Punkt an, an dem die Gerade die x-Achse schneidet.
4. Können lineare Funktionen mehr als eine Nullstelle haben?
Nein, lineare Funktionen haben höchstens eine Nullstelle, da sie eine gerade Linie darstellen.
5. Warum sind Nullstellen wichtig?
Nullstellen sind wichtig, um zu verstehen, wo eine Funktion ihre Werte wechselt (von positiv zu negativ oder umgekehrt).
Zusammenfassung
Die Nullstellen einer linearen Funktion sind die x-Werte, bei denen der Funktionswert y gleich null ist.
Sie geben an, wo die Gerade die x-Achse schneidet. Um die Nullstellen zu finden, setzt man die Funktionsgleichung gleich null und löst die Gleichung nach x auf.
Diese Konzepte sind wichtig in der Mathematik, Physik und Wirtschaft, um Schnittpunkte und Wechselpunkte von Funktionen zu bestimmen.
In der folgenden Lerneinheiten schauen wir uns an, wie du den Schnittpunkt zweier linearer Funktionen bestimmen kannst.
Was gibt es noch bei uns?
Optimaler Lernerfolg durch tausende Übungsaufgaben
Quizfrage 1
Quizfrage 2
“Wusstest du, dass unter jedem Kursabschnitt eine Vielzahl von verschiedenen interaktiven Übungsaufgaben bereitsteht, mit denen du deinen aktuellen Wissensstand überprüfen kannst?”
Was ist Technikermathe?
Unser Dozent Jan erklärt es dir in nur 2 Minuten!
Oder direkt den > kostenlosen Probekurs < durchstöbern? – Hier findest du Auszüge aus jedem unserer Kurse!
Geballtes Wissen in derzeit 26 Kursen
Hat dir dieses Thema Nullstelle berechnen gefallen? – Ja? – Dann schaue dir auch gleich die anderen Themen zu den Kursen
WT3 (Werkstoffprüfung) und
TM1 (Technische Mechanik – Statik) an.
Perfekte Prüfungsvorbereitung für nur 14,90 EUR/Jahr pro Kurs
++ Günstiger geht’s nicht!! ++
Oder direkt Mitglied werden und Zugriff auf alle 26 Kurse (inkl. Webinare + Unterlagen) sichern ab 7,40 EUR/Monat ++ Besser geht’s nicht!! ++
Social Media? - Sind wir dabei!
Dein Technikermathe.de-Team