In dieser Lerneinheit wollen wir uns mal anschauen, wie du die Funktionsgleichung bestimmen von linearen Funktionen kannst.
Für ein optimales Verständnis helfen dir zwei Videoclips und mehrere ausführliche Beispiele mit Zahlenwerten zu dem Thema. Mehr zu diesem Thema und der Mathematik findest du im Kurs: Ma2-Lineare Gleichungssysteme: Oder lieber mit den Grundlagen starten? Alles dazu findest du im Kurs: Ma1-Grundlagen der Mathematik
Du weißt aus der vorherigen Lerneinheit bereits wie die Steigung und der Steigungswinkel von linearen Funktionen berechnet wird.
Funktionsgleichung bestimmen – Grundlagen
Die Funktionsgleichung einer linearen Funktion kannst du bestimmen, wenn du
- die Steigung
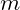 und den Schnittpunkt der Funktion mit der y-Achse
und den Schnittpunkt der Funktion mit der y-Achse 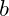 kennst.
kennst. - die Steigung
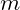 und einen Punkt P auf dem linearen Funktionsgraphen kennst.
und einen Punkt P auf dem linearen Funktionsgraphen kennst. - den Schnittpunkt der Funktion mit der y-Achse
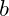 und einen Punkt P auf dem linearen Funktionsgraphen kennst.
und einen Punkt P auf dem linearen Funktionsgraphen kennst. - zwei Punkte auf dem linearen Funktionsgraphen kennst.
Was ist die Funktionsgleichung einer linearen Funktion?
Die Funktionsgleichung einer linearen Funktion ist eine mathematische Darstellung einer Geraden. Sie hat die Form: ![]() wobei
wobei ![]() der Funktionswert,
der Funktionswert, ![]() die unabhängige Variable,
die unabhängige Variable, ![]() die Steigung der Geraden und
die Steigung der Geraden und ![]() der y-Achsenabschnitt ist.
der y-Achsenabschnitt ist.
Für die Angabe der Funktionsgleichung müssen die Steigung ![]() und der Schnittpunkt der Funktion mit der y-Achse
und der Schnittpunkt der Funktion mit der y-Achse ![]() bekannt sein. Wir schauen uns alle drei Varianten in dieser Lerneinheit mal genauer an. Außerdem zeigen wir dir, wie du bestimmst, ob bestimmte Punkte auf einer linearen Funktion liegen oder nicht.
bekannt sein. Wir schauen uns alle drei Varianten in dieser Lerneinheit mal genauer an. Außerdem zeigen wir dir, wie du bestimmst, ob bestimmte Punkte auf einer linearen Funktion liegen oder nicht.
Funktionsgleichung bestimmen | Steigung und Schnittpunkt bekannt

Wir wollen für die obige lineare Funktion die Funktionsgleichung bestimmen. Die Steigung beträgt ![]() , der Schnittpunkt mit der y-Achse ist bei
, der Schnittpunkt mit der y-Achse ist bei ![]() gegeben. Wir können nun mittels der Steigung
gegeben. Wir können nun mittels der Steigung ![]() und dem Schnittpunkt der Funktion mit der
und dem Schnittpunkt der Funktion mit der ![]() -Achse die Funktionsgleichung der obigen Funktion bestimmen.
-Achse die Funktionsgleichung der obigen Funktion bestimmen.
Für den Schnittpunkt der Funktion mit der y-Achse ist der x-Wert immer Null. Es gilt also immer der Punkt (0 | b). In unserem Beispiel also (0 | -3).
Für die Steigung haben wir ![]() ermittelt. Wir können nun aus der Steigung und dem Schnittpunkt mit der y-Achse für die lineare Funktion die Funktionsgleichung bestimmen. Dazu betrachten wir die allgemeine Funktionsgleichung:
ermittelt. Wir können nun aus der Steigung und dem Schnittpunkt mit der y-Achse für die lineare Funktion die Funktionsgleichung bestimmen. Dazu betrachten wir die allgemeine Funktionsgleichung:
![]() bzw.
bzw.
![]()
Wir setzen nun ![]() und
und ![]() ein:
ein:
![]()
Und haben die Funktionsgleichung der obigen Funktion bestimmt. Wir können nun wieder für ![]() alle reellen Zahlen einsetzen und erhalten dann den dazugehörigen Funktionswert. Setzen wir zum Beispiel für
alle reellen Zahlen einsetzen und erhalten dann den dazugehörigen Funktionswert. Setzen wir zum Beispiel für ![]() ein, so erhalten wir:
ein, so erhalten wir:
![]()
Der Punkt (1|6) befindet sich auf dem linearen Funktionsgraphen.
Der Funktionsgraph einer linearen Funktion ist immer eine Gerade bzw. geradlinig.
Der Schnittpunkt zwischen linearer Funktion und der y-Achse weist hierbei stets die Koordinaten P(0|b) auf.
Für die Steigung ![]() einer linearen Funktion musst du dir merken, dass im Nenner der Schritt in x-Richtung und im Zähler die Schritte in y-Richtung stehen.
einer linearen Funktion musst du dir merken, dass im Nenner der Schritt in x-Richtung und im Zähler die Schritte in y-Richtung stehen.
Funktionsgleichung bestimmen | Steigung und Punkt bekannt

In der obigen Grafik ist die Steigung der linearen Funktion gegeben sowie ein Punkt auf der Funktion. Wir können mittels der allgemeinen Funktionsgleichung für lineare Funktionen die Funktionsgleichung der obigen Funktion aus der gegebenen Steigung und dem gegebenen Punkt bestimmen. Dazu setzen wir die Steigung ![]() und den Punkt P(5|-11) in die Funktionsgleichung ein:
und den Punkt P(5|-11) in die Funktionsgleichung ein:
![]()
Ein Punkt P(x|y) bzw. P(x | f(x)) wird so eingesetzt, dass der erste Wert anstelle von ![]() eingesetzt wird und der zweite Wert anstelle von
eingesetzt wird und der zweite Wert anstelle von ![]() bzw.
bzw. ![]() . Der Punkt (5|-11) wird also wie folgt eingesetzt:
. Der Punkt (5|-11) wird also wie folgt eingesetzt:
![]()
Wir können nun ![]() berechnen, indem wir die Funktionsgleichung nach
berechnen, indem wir die Funktionsgleichung nach ![]() auflösen:
auflösen:
![]()
![]() |
|![]()
![]()
![]()
Der Schnittpunkt der Funktion mit der y-Achse ist bei ![]() gegeben. Die Funktionsgleichung für die obige Funktion beträgt also:
gegeben. Die Funktionsgleichung für die obige Funktion beträgt also:
![]()
Bei dieser Vorgehensweise ist der Schnittpunkt mit der ![]() -Achse nicht bekannt und muss zunächst berechnet werden.
-Achse nicht bekannt und muss zunächst berechnet werden.
Funktionsgleichung bestimmen | Punkt und Schnittpunkt bekannt

In der obigen Grafik ist ein Punkt auf der linearen Funktion gegeben sowie der Schnittpunkt der Funktion mit der y-Achse. Nicht gegeben ist die Steigung ![]() , welche wir zunächst berechnen müssen. Dazu verwenden wir wieder die allgemeine Funktionsgleichung einer linearen Funktion und setzen den Punkt P(-5 | 7,5) und den Schnittpunkt b = -1,5 in diese ein:
, welche wir zunächst berechnen müssen. Dazu verwenden wir wieder die allgemeine Funktionsgleichung einer linearen Funktion und setzen den Punkt P(-5 | 7,5) und den Schnittpunkt b = -1,5 in diese ein:
![]()
![]() |
|![]()
![]()
![]() |
|![]()
![]()
![]()
Die Steigung der Funktion beträgt ![]() . Wir erhalten damit die folgende Funktionsgleichung:
. Wir erhalten damit die folgende Funktionsgleichung:
![]()
Nachdem du nun weißt, wie die Funktionsgleichung einer linearen Funktion bestimmt wird, wollen wir uns nun noch anschauen, wie du herausfindest, ob bestimmte Punkte auf einer Funktion liegen oder nicht.
Funktionsgleichung bestimmen | Zwei Punkte bekannt

Gegeben seien die beiden Punkte P(-2|10) und Q(4|-10), die beide auf der linearen Funktion liegen. Du kannst nun mithilfe dieser beiden Punkte den Funktionsgraphen zeichnerisch bestimmen, indem du beide Punkte miteinander verbindest und die Funktion verlängerst. Willst du hingegen die Funktionsgleichung bestimmen, dann musst du zunächst die Steigung berechnen. Die Steigung aus zwei Punkten wird wie folgt berechnet:
![]()
Du ziehst also einfach die y-Werte und die x-Werte der beiden Punkte voneinander ab. Wichtig ist hierbei nur, dass der y-Wert und der x-Wert desselben Punktes untereinander liegen!
Die Steigung beträgt für die obige Funktion:
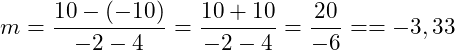
Die Steigung der Funktion beträgt ![]() . Es liegt eine negative Steigung vor, damit ist die Funktion fallend. Um nun die Funktionsgleichung zu bestimmen, kannst du wie bereits oben gezeigt vorgehen und in die Funktionsgleichung einen der beiden Punkte sowie die Steigung einsetzen, um den Schnittpunkt
. Es liegt eine negative Steigung vor, damit ist die Funktion fallend. Um nun die Funktionsgleichung zu bestimmen, kannst du wie bereits oben gezeigt vorgehen und in die Funktionsgleichung einen der beiden Punkte sowie die Steigung einsetzen, um den Schnittpunkt ![]() mit der y-Achse zu bestimmen:
mit der y-Achse zu bestimmen:
![]()
![]() |
|![]()
![]()
Die Funktionsgleichung lautet demnach:
![]()
Videoclip | Funktionsgleichung aus zwei Punkten bestimmen
Im folgenden Video zeigt dir Jessica, wie du die Funktionsgleichung aus zwei Punkten bestimmst.
Beispiel | Funktionsgleichung bestimmen
Sollst du herausfinden, ob Punkte auf einer Funktion liegen, so setzt du den ![]() -Wert in die gegebene Funktionsgleichung ein und schaust, ob derselbe Funktionswert resultiert, wie im Punkt angegeben. Schauen wir uns dazu mal ein Beispiel an:
-Wert in die gegebene Funktionsgleichung ein und schaust, ob derselbe Funktionswert resultiert, wie im Punkt angegeben. Schauen wir uns dazu mal ein Beispiel an:
Gegeben sei die lineare Funktion ![]() . Prüfe ob die folgenden Punkte auf der Funktion liegen:
. Prüfe ob die folgenden Punkte auf der Funktion liegen:
(4|30), (5|35), (16,4|61), (14,8|61)
[/su_service] [/su_box]
Du setzt nun die x-Werte der Punkte in die gegebene Funktion ein:
(4|30):
Punkt liegt auf der Funktion
(5|35):
Punkt liegt nicht auf der Funktion
(16,4|61):
Punkt liegt auf der Funktion
(14,8|61):
Punkt liegt nicht auf der Funktion
Ist der Funktionswert mit dem zweiten Wert des Punktes identisch, dann liegt der Punkt auf der Funktion, ansonsten nicht.
Anwendung der Funktionsgleichung von linearen Funktionen
- Mathematik: Analyse und Darstellung von Geraden.
- Physik: Berechnung von Bewegungen und Geschwindigkeiten.
- Wirtschaft: Erstellung von Prognosen und Analysen.
Mögliche Fragestellungen | Häufig gestellte Fragen (FAQs)
1. Was ist die Funktionsgleichung einer linearen Funktion?
- Die Funktionsgleichung beschreibt eine Gerade im Koordinatensystem und hat die Form
 .
.
2. Wie berechnet man die Steigung?
- Die Steigung wird berechnet, indem die Differenz der y-Werte durch die Differenz der x-Werte zweier Punkte auf der Geraden geteilt wird.
3. Was ist der y-Achsenabschnitt?
- Der y-Achsenabschnitt ist der Punkt, an dem die Gerade die y-Achse schneidet.
4. Wie stellt man die Funktionsgleichung auf?
- Berechne die Steigung, finde den y-Achsenabschnitt und setze diese Werte in die Gleichung
 ein.
ein.
5. Warum sind diese Berechnungen wichtig?
- Diese Berechnungen sind wichtig für das Verständnis und die Analyse von linearen Zusammenhängen in verschiedenen Bereichen.
Zusammenfassung
Die Funktionsgleichung einer linearen Funktion beschreibt eine Gerade im Koordinatensystem und hat die Form ![]() . Die Steigung
. Die Steigung ![]() gibt an, wie stark die Gerade ansteigt oder abfällt, während der y-Achsenabschnitt
gibt an, wie stark die Gerade ansteigt oder abfällt, während der y-Achsenabschnitt ![]() den Punkt angibt, an dem die Gerade die y-Achse schneidet.
den Punkt angibt, an dem die Gerade die y-Achse schneidet.
Die Bestimmung der Funktionsgleichung erfolgt durch Berechnung der Steigung und des y-Achsenabschnitts, basierend auf zwei Punkten auf der Geraden.
In der folgenden Lerneinheit schauen wir uns an, wie die Nullstellen von linearen Funktionen bestimmt werden.
Was gibt es noch bei uns?
Optimaler Lernerfolg durch tausende Übungsaufgaben

Quizfrage 1
Quizfrage 2
“Wusstest du, dass unter jedem Kursabschnitt eine Vielzahl von verschiedenen interaktiven Übungsaufgaben bereitsteht, mit denen du deinen aktuellen Wissensstand überprüfen kannst?”
Was ist Technikermathe?
Unser Dozent Jan erklärt es dir in nur 2 Minuten!
Oder direkt den > kostenlosen Probekurs < durchstöbern? – Hier findest du Auszüge aus jedem unserer Kurse!
Geballtes Wissen in derzeit 26 Kursen
Hat dir dieses Thema gefallen? – Ja? – Dann schaue dir auch gleich die anderen Themen zu den Kursen
WT3 (Werkstoffprüfung) und
TM1 (Technische Mechanik – Statik) an.


Perfekte Prüfungsvorbereitung für nur 14,90 EUR/Jahr pro Kurs
++ Günstiger geht’s nicht!! ++
Oder direkt Mitglied werden und Zugriff auf alle 26 Kurse (inkl. Webinare + Unterlagen) sichern ab 7,40 EUR/Monat ++ Besser geht’s nicht!! ++
Social Media? - Sind wir dabei!
Dein Technikermathe.de-Team


![MA2 - Funktionsgleichung von linearen Funktionen bestimmen [Grundlagen, Videoclips, Aufgaben & Tipps] 1 Funktionsgleichung linearer Funktionen](https://technikermathe.de/wp-content/uploads/2020/04/tk-funktionsgleichung-768x432.jpg)




