MA1 – Eigenschaften von Mengen [Grundlagen, Erklärung, Videoclips, Aufgaben & Tipps]

In dieser Lerneinheit betrachten wir einige Eigenschaften von Mengen.

Mengen – Grundlagen

Nachdem wir gelernt haben, was die aufzählende und beschreibende Mengenschreibweise ist, betrachten wir in dieser Lerneinheit einmal die unterschiedlichen Eigenschaften von Mengen.

Eigenschaften von Mengen – Unterscheidung von Mengen

• Eine Menge 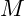die mindestens ein Elemente enthält wird als nicht leere Menge bezeichnet. Enthält eine Menge kein Element, so wird sie als leer bezeichnet.
  
  . Es gibt kein Element für x, welches die Gleichung erfüllt. Egal welche Zahl für x eingesetzt wird, die Gleichung nimmt niemals den Wert Null an. Damit handelt es sich hierbei um eine leere Menge.

• Eine Menge die keine Elemente oder abzählbare Elemente enthält bezeichnen wir als endliche Menge. Eine Menge mit nicht abzählbaren Elementen (also unendlichen Elementen), bezeichnen wir als unendliche Menge.
  
  Die Menge ist endlich. Da hier die natürlichen Zahlen (positive ganze Zahlen) betrachtet werden die kleiner als 12 sind, ist die Menge abzählbar (einsetzen von x = 1 bis x = 6) : .
  
  Die Menge hingegen ist unendlich, da hier keine Obergrenze angegeben ist. Alle natürlichen Zahlen größer als 12 werden hier berücksichtigt.

Eigenschaften vom Mengen – Mächtigkeit von Mengen

Die Mächtigkeit von Mengen wird durch die Anzahl der Elemente bestimmt:

Die Mächtigkeit einer Menge wird durch Betragsstriche angegeben:

M = |Anzahl Elemente|

Besitzen die beiden Mengen $A$ und $B$ die gleiche Mächtigkeit?

A = {x,y,z} | B = {5,10,15,20}

Die Menge A weist 3 Elemente auf. Die Mächtigkeit beträgt: A = |3|

Die Menge B weist 4 Elemente auf. Die Mächtigkeit beträgt: B = |4|

Die beiden Menge weisen nicht die gleiche Mächtigkeit auf.

Eigenschaften von Mengen – Gleichheit von Mengen

Zwei Mengen sind dann gleich, wenn die Elemente beider Mengen identisch sind.

Sind die beiden Mengen gleich?

A = {2,3,4,5,6,7} | B = {2,3,4,6,7}

Beide Mengen sind nicht gleich, da die Elemente aus A nicht alle in B enthalten sind. Man schreibt dann:

Sind die beiden Mengen gleich?

A = {a,b,c,d,e} | B = {a,b,c,d,e}

Hier sind beiden Mengen gleich. Alle Elemente aus A sind in B enthalten und umgekehrt. Man schreibt dann:

Man schreibt auch:

Gelesen: Die Menge A ist gleich der Menge B, wenn A Teilmenge () der Menge B ist und () B Teilmenge () der Menge A.

Unvergleichbare Mengen

Zwei Mengen sind unvergleichbar, wenn keine Menge ein Element der anderen Menge enthält. 

Sind die beiden Mengen unvergleichbar?

A = {2,3,4,5} | B = {1,6,7,8}

Beide Mengen sind unvergleichbar, da kein Elemente aus A auch in B enthalten ist und umgekehrt.

Man schreibt auch:

Gelesen: Die Menge A ist nicht gleich () der Menge B, wenn A nicht Teilmenge () der Menge B ist und () B nicht Teilmenge () der Menge A.

Darstellung von Mengen | Mengendiagramm, Venn-Diagramm

Mengen können in einem Mengendiagramm (auch: Venn-Diagramm) dargestellt werden. Sie sind vor allem im späteren Vergleich von mehreren Mengen relevant. Grundsätzlich werden bei den Mengendiagrammen die Elemente einer Menge innerhalb eines Kreises oder einer Ellipse dargestellt:

In der obigen Grafik siehst du die beiden Mengen A und B und die Elemente dieser Mengen. Du kannst auf den ersten Blick erkennen, dass innerhalb der Menge A die Menge aller Elemente, die größer gleich 7 und kleiner gleich 49 sowie durch 7 teilbar sind, enthalten sind. In der Menge B finden sich alle Elemente, die größer gleich 12 und kleiner gleich 32 sowie durch 4 teilbar sind. Elemente die nicht zu diesen Mengen zählen sind außerhalb der Mengen abgebildet. Außerdem sind die gegebenen Elemente alle ganzzahlig und positiv. Damit sind hier nur natürliche Zahlen gegeben.

Es gilt also für die Menge A:

A = {7,14,21,28,35,42,49}

bzw.

Für die Menge B gilt dann:

B = {12,16,20,24,28,32}

bzw.

Du kannst natürlich auch mit größer als und kleiner als arbeiten, dann gilt:

Da x größer als 8 ist und wir nur natürliche Zahlen betrachten, die durch 4 teilbar sind, startest du mit der nächst größeren Zahl, also der 16. Deine letzte Zahl ist kleiner als 36 und durch 4 teilbar. Also endet die Menge mit der nächst kleineren Zahl, die durch 4 teilbar ist, also der 32.

Mengenoperationen

Betrachtest du die Beziehung zwischen zwei Mengen so können wir die vier Möglichkeiten betrachten:

• Teilmenge 
• Schnittmenge
• Vereinigungsmenge
• Differenzmenge

Mögliche Fragestellungen | Häufig gestellte Fragen (FAQs)

Zusammenfassung

Das Rechnen mit Mengen umfasst grundlegende Operationen wie Vereinigungsmenge, Schnittmenge, Differenzmenge und Komplementmenge. Diese Operationen helfen, die Beziehungen zwischen verschiedenen Mengen zu verstehen und komplexe mathematische Probleme zu lösen. Mit diesen Kenntnissen kannst du schnell und korrekt mit Mengen arbeiten.

Was gibt es noch bei uns?

Optimaler Lernerfolg durch tausende Übungsaufgaben

 

Quizfrage 1

 

Quizfrage 2

 

“Wusstest du, dass unter jedem Kursabschnitt eine Vielzahl von verschiedenen interaktiven Übungsaufgaben bereitsteht, mit denen du deinen aktuellen Wissensstand überprüfen kannst?”  

Alle Technikerschulen im Überblick

 

Kennst du eigentlich schon unser großes Technikerschulen-Verzeichnis für alle Bundesländer mit allen wichtigen Informationen (Studiengänge, Kosten, Anschrift, Routenplaner, Social-Media) ? Nein? – Dann schau einfach mal hinein:   

Geballtes Wissen in derzeit 26 Kursen

Hat dir dieses Thema gefallen? – Ja? – Dann schaue dir auch gleich die anderen Themen zu den Kursen 

WT3 (Werkstoffprüfung) und
TM1 (Technische Mechanik – Statik) an. 

 

Perfekte Prüfungsvorbereitung für nur 14,90 EUR/Jahr pro Kurs

++ Günstiger geht’s nicht!! ++

 

 

Oder direkt Mitglied werden und Zugriff auf alle 26 Kurse  (inkl.  Webinare  + Unterlagen) sichern ab 7,40 EUR/Monat  ++ Besser geht’s nicht!! ++  

Dein Technikermathe.de-Team