MA1 – Nenner rational machen [Grundlagen, Erklärung, Beispiele, Lernclips]

In dieser Lerneinheit schauen wir uns anschauen, wie du den Nenner rational machen [Rationalisieren des Nenners] kannst. Dazu betrachten wir einen Bruch, welcher im Nenner eine Wurzel (eine irrationale Zahl) enthält und wollen diese Wurzel aus dem Nenner entfernen.

Für ein optimales Verständnis helfen dir zwei Videoclips und mehrere ausführliche Beispiele mit Zahlenwerten zu dem Thema.

Mehr zu diesem Thema und der Mathematik findest du im Kurs: Ma1-Grundlagen der Mathematik

Auch interessant! Alles zu Linearen Gleichungen findest du im Kurs: Ma2-Lineare Gleichungssysteme

Nenner rational machen [Rationalisieren des Nenners] – Überblick

Nenner rational machen | Grundlagen, Erklärung

Haben wir einen Bruch mit einer Wurzel im Nenner gegeben, so ist der Nenner irrational:

Bruch mit irrationalem Nenner

$\dfrac{1}{\sqrt{2}}$

Das Rationalisieren des Nenners ist ein wichtiger Schritt in der Mathematik, um Brüche zu vereinfachen. Dabei wird der Nenner eines Bruchs so umgeformt, dass keine Wurzel mehr im Nenner steht.

Was bedeutet “Nenner rational machen”?

Beim Rationalisieren des Nenners wird ein Bruch so umgeformt, dass keine Wurzeln im Nenner mehr vorhanden sind. Dies geschieht durch Multiplikation des Bruchs mit einem geeigneten Wert, der die Wurzel im Nenner beseitigt.

Eine Wurzel ist nichts anderes als eine irrationale Zahl. Ziel dieser Lerneinheit ist es nun, den Nenner rational zu machen, d.h. dort soll statt einer irrationalen Zahl eine rationale Zahl stehen. Wir wollen also die Wurzel aus dem Nenner entfernen.

Du kennst bereits die Wurzelgesetze und weißt wie man Wurzeln gleichnamig macht. Wir wollen uns in dieser Lerneinheit mal anschauen, wie du eine im Nenner gegebene Wurzel in den Zähler überführst. Dazu musst du die bereits erlernten Vorkenntnisse haben:

Erweitern und Kürzen von Brüchen

Binomische Formel

Beide Themen haben wir bereits in den vorangegangenen Lerneinheiten innerhalb dieses Kurses ausführlich besprochen.

Wir wollen dazu folgende drei Fälle betrachten:

Quadratwurzel im Nenner entfernen.
Höhere Wurzel im Nenner entfernen.
Summe/Differenz von Wurzeln im Nenner entfernen.

Nenner rational machen: Quadratwurzeln

Nenner rational machen | Quadratwurzel im Nenner - mit Nenner erweitern — Nenner rational machen | Quadratwurzel im Nenner – mit Nenner erweitern

Gegeben sei der folgende Bruch mit einer Quadratwurzel (Wurzel mit dem Grad 2) im Nenner:

$\dfrac{1}{\sqrt{3}}$

Wir wollen nun die Wurzel aus dem Nenner entfernen. Dies können wir mit dem Erweitern von Brüchen erreichen. Dazu erweitern wir den gegebenen Bruch mit der im Nenner stehenden Quadratwurzel:

$\dfrac{1}{\sqrt{3}} \cdot \dfrac{\sqrt{3}}{\sqrt{3}}$

$= \dfrac{1 \cdot \sqrt{3}}{\sqrt{3} \cdot \sqrt{3}}$

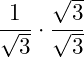
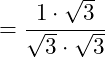
Wir wenden als nächstes die Wurzelgesetze auf die Wurzeln im Nenner an. Da es sich um die Multiplikation zweier Wurzeln mit demselben Grad handelt, können wir aus zwei Wurzeln eine Wurzel machen:

$\dfrac{\sqrt{3}}{\sqrt{3} \cdot \sqrt{3}}$

$= \dfrac{\sqrt{3}}{\sqrt{3 \cdot 3}}$

$= \dfrac{\sqrt{3}}{\sqrt{3^2}}$

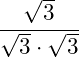
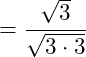
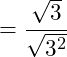
Der Radiant im Nenner weist den Exponenten 2 auf. Die Wurzel weist den Wurzelgrad 2 auf, betrachten wir die Potenzdarstellung der Wurzel im Nenner, so gilt:

Wurzel im Nenner:

$\sqrt{3^2} = 3^{\frac{2}{2}} = 3^1 = 3$

Da Exponent des Radianten und Wurzelgrad gleich groß sind, heben sich beide gegenseitig auf und es verbleibt der Radiant:

$\dfrac{\sqrt{3}}{3}$

Wir haben die Wurzel im Nennern in den Zähler überführt, wir haben also den Nenner rational gemacht.

Beispiel: Quadratwurzeln im Nenner

Beispiel: Quadratwurzeln im Nenner!

Gegeben sei der folgende Bruch:

$\dfrac{2}{\sqrt{5}}$

Mach den Nenner rational!

1. Erweitern des Bruchs mit der Quadratwurzel:

$\dfrac{2}{\sqrt{5}} \cdot \dfrac{\sqrt{5}}{\sqrt{5}}$

$=\dfrac{2 \cdot \sqrt{5}}{\sqrt{5} \cdot \sqrt{5}}$

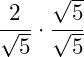
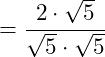
2. Anwendung der Wurzelgesetze der Multiplikation von zwei Wurzeln mit gleichem Grad:

$\dfrac{2\sqrt{5}}{\sqrt{5 \cdot 5} }$

$= \dfrac{2\sqrt{5}}{\sqrt{5^2} }$

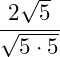
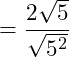
3. Grad der Wurzel und Exponent des Radianten sind gleich, damit fallen Wurzel und Exponent im Nenner weg:

$\dfrac{2\sqrt{5}}{5}$

Der Nenner ist rational, weil keine irrationale Zahl im Nenner steht.

Videoclip 1: Nenner rational machen (Quadratwurzel)

Im folgenden Video zeigen wir dir, wie du einen Nenner mit Quadratwurzel rational machst.

Lernclip | Nenner rational machen

Nenner rational machen: Höhere Wurzeln

Rationalisieren des Nenners | Wurzel m-ten Grades im Nenner

Wir wollen uns nun anschauen, wie du eine Wurzel mit höheren Wurzelgrad rational machen kannst. Betrachten wir dazu den folgenden Bruch:

$\dfrac{1}{\sqrt[3]{5}}$

Auch hier musst du das Erweitern von Brüchen anwenden. Eine Wurzel mit dem Wurzelgrad m erweiterst du m-1 mal. Hat die Wurzel also den Wurzelgrad m = 3, dann musst du 3-1 = 2 mal erweitern. Eine Wurzel mit Wurzelgrad 4 muss demnach 3 mal erweitert werden usw.

Betrachten wir wieder unseren Bruch. Hier ist eine Wurzel im Nenner mit Wurzelgrad 3 gegeben. Somit müssen wir diese 2 mal erweitern:

$\dfrac{\sqrt[3]{5}}{\sqrt[3]{5}} \cdot \dfrac{\sqrt[3]{5}}{\sqrt[3]{5}} = (\dfrac{\sqrt[3]{5}}{\sqrt[3]{5}})^2 = \dfrac{(\sqrt[3]{5})^2}{(\sqrt[3]{5})^2}$

Du musst also nun nicht zwei mal die Erweiterung zufügen, sondern kannst die Wurzel im Zähler und im Nenner entsprechend Potenzieren (hier mit m-1 = 2):

$\dfrac{1}{\sqrt[3]{5}} \cdot \dfrac{(\sqrt[3]{5})^2}{(\sqrt[3]{5})^2}$

Du kannst hier das Wurzelgesetz des Potenzierens anwenden (Exponent wird zum Radianten gezogen):

$\dfrac{1}{\sqrt[3]{5}} \cdot \dfrac{\sqrt[3]{5^2}}{\sqrt[3]{5^2}}$

Als nächstes wendest du wieder das das Wurzelgesetz der Multiplikation an. Du kannst also das Produkt im Nenner unter eine Wurzel schreiben, weil beide Wurzeln den selben Grad aufweisen:

$\dfrac{1 \cdot \sqrt[3]{5^2} }{\sqrt[3]{5} \cdot \sqrt[3]{5^2}}$

$\dfrac{\sqrt[3]{5^2} }{\sqrt[3]{5 \cdot 5^2}}$

$\dfrac{\sqrt[3]{5^2} }{\sqrt[3]{5^3}}$

Grad der Wurzel und Exponent des Radianten sind wieder gleich, damit fallen Wurzel und der Exponent im Nenner weg:

$\dfrac{\sqrt[3]{5^2} }{5}$

Der Nenner ist rational.

Beispiel: Höhere Wurzel im Nenner

Beispiel: Höhere Wurzel im Nenner!

Gegeben sei der folgende Bruch mit irrationalem Nenner:

$\dfrac{5}{\sqrt[4]{7}}$

Mach den Nenner rational!

1. Der Bruch weist einen Wurzelgrad von m = 4 auf, damit müssen wir 3-mal erweitern:

$\dfrac{5}{\sqrt[4]{7}} \cdot \dfrac{(\sqrt[4]{7})^3}{(\sqrt[4]{7})^3}$

2. Durch Anwendung der Wurzelgesetze (Potenzieren), können wir den Exponenten der Wurzel in die Wurzel ziehen:

$\dfrac{5}{\sqrt[4]{7}} \cdot \dfrac{\sqrt[4]{7^3}}{\sqrt[4]{7^3}}$

$\dfrac{5 \cdot \sqrt[4]{7^3}}{\sqrt[4]{7} \cdot \sqrt[4]{7^3}}$

3. Anwendung der Wurzelgesetze der Multiplikation von zwei Wurzeln mit gleichem Grad:

$\dfrac{5 \cdot \sqrt[4]{7^3}}{\sqrt[4]{7 \cdot 7^3}}$

$\dfrac{5 \cdot \sqrt[4]{7^3}}{\sqrt[4]{7^4}}$

4. Grad der Wurzel und Exponent des Radianten im Nenner sind gleich, damit fallen Wurzel und Exponent im Nenner weg:

$\dfrac{5 \sqrt[4]{7^3}}{7}$

Der Nenner des Bruchs ist rational.

Videoclip 2: Nenner rational machen (höhere Wurzel)

Im folgenden Video zeigen wir dir, wie du einen Nenner rational machen kannst, wenn eine höhere Wurzel im Nenner gegeben ist.

Lernclip: Nenner rational machen

Nenner rational machen: Summen/Differenzen

Um den Nenner eines Bruchs rational zu machen, in welchem eine Summe bzw. eine Differenz mit zwei Gliedern enthalten sind (wovon mindestens ein Glied eine Wurzel ist), benötigst du die 3. binomische Formel.

Merk’s dir!

Wir betrachten bei dieser Variante nur Quadratwurzeln im Nenner .

Summen im Nenner

Hierzu betrachten wir den folgenden Bruch:

Bruch mit Summe und irrationaler Zahl im Nenner

$\dfrac{1}{2 + \sqrt{5}}$

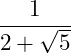
Wir wollen den Nenner rational machen. Dazu erweitern wir mit dem Nenner, wobei aus der Summe eine Differenz wird, d.h. aus dem Pluszeichen ein Minuszeichen:

$\dfrac{1}{2 + \sqrt{5}} \cdot \dfrac{2 - \sqrt{5}}{2 - \sqrt{5}}$

$\dfrac{1 \cdot (2 - \sqrt{5}) }{(2 + \sqrt{5}) \cdot (2 - \sqrt{5})}$

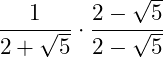
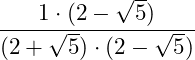
Auf den Nenner kannst du nun die 3. binomische Formel zum Klammern auflösen anwenden:

$\dfrac{1 \cdot (2 - \sqrt{5}) }{4 - \sqrt{5}^2 }$

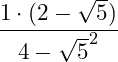
Das Wurzelgesetz des Potenzierens anwenden und den Exponenten in die Wurzel ziehen:

$\dfrac{1 \cdot (2 - \sqrt{5}) }{4 - \sqrt{5^2}}$

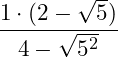
Der Wurzelgrad der Wurzel im Nenner und der Exponent des Radianten sind gleich groß, damit verbleibt der Radiant:

$\dfrac{1 \cdot (2 - \sqrt{5}) }{4 - 5}$

$\dfrac{1 \cdot (2 - \sqrt{5}) }{-1}$

$-(2 - \sqrt{5})$

$-2 + \sqrt{5}$

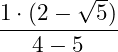
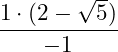
In diesem Beispiel fällt der gesamte Nenner weg.

Beispiel: Summen/Differenzen im Nenner

Schauen wir uns ein weiteres Beispiel an:

Beispiel: Summen/Differenzen im Nenner!

Gegeben sei der folgende Bruch:

$\dfrac{5}{\sqrt{5} + \sqrt{11}}$

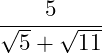
Mach den Nenner rational!

1. Im ersten Schritt erweitern wir den Bruch mit dem Nenner, wobei aus der Summe eine Differenz wird:

$\dfrac{5}{\sqrt{5} + \sqrt{11}} \cdot \dfrac{\sqrt{5} - \sqrt{11}}{\sqrt{5} - \sqrt{11}}$

$\dfrac{5 \cdot (\sqrt{5} - \sqrt{11})}{(\sqrt{5} + \sqrt{11}) \cdot (\sqrt{5} - \sqrt{11})}$

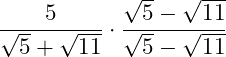
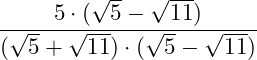
2. Danach wendest du im Nenner die 3. Binomische Formel an:

$\dfrac{5 \cdot (\sqrt{5} - \sqrt{11})}{\sqrt{5}^2 - \sqrt{11}^2}$

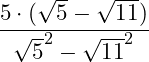
3. Als nächstes ziehst du den Exponenten in die Wurzel (Wurzelgesetze: Potenzieren):

$\dfrac{5 \cdot (\sqrt{5} - \sqrt{11})}{\sqrt{5^2} - \sqrt{11^2}}$

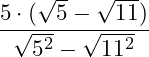
Sowohl der Grad der Wurzeln im Nenner als auch die Exponenten der Radianten weisen den Grad 2 auf, demnach fallen Wurzeln und Exponenten weg:

$\dfrac{5 \cdot (\sqrt{5} - \sqrt{11})}{5 - 11}$

$\dfrac{5 \cdot (\sqrt{5} - \sqrt{11})}{-6}$

$-\dfrac{5 \cdot (\sqrt{5} - \sqrt{11})}{6}$

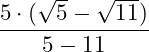
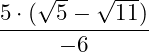
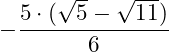
Der Nenner ist rational.

Differenzen im Nenner

Für die Anwendung von Differenzen im Nenner gilt, dass aus der Differenz eine Summe wird:

Beispiel: Summen/Differenzen im Nenner

Schauen wir uns ein weiteres Beispiel an:

Beispiel: Summen/Differenzen im Nenner!

Gegeben sei der folgende Bruch:

$\dfrac{\sqrt{3}}{\sqrt{7} - \sqrt{12}}$

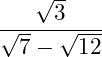
Mach den Nenner rational!

1. Im ersten Schritt erweitern wir den Bruch mit dem Nenner, wobei aus der Differenz eine Summe wird:

$\dfrac{\sqrt{3}}{\sqrt{7} - \sqrt{12}} \cdot \dfrac{\sqrt{7} + \sqrt{12}}{\sqrt{7} + \sqrt{12}}$

$\dfrac{\sqrt{3} \cdot (\sqrt{7} + \sqrt{12})}{(\sqrt{7} - \sqrt{12}) \cdot (\sqrt{7} + \sqrt{12})}$

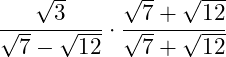
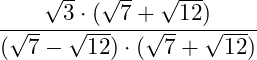
2. Danach wendest du im Nenner die 3. Binomische Formel an:

$\dfrac{\sqrt{3} \cdot (\sqrt{7} + \sqrt{12})}{\sqrt{7}^2 - \sqrt{12}^2}$

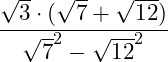
3. Als nächstes ziehst du den Exponenten in die Wurzel (Wurzelgesetze: Potenzieren):

$\dfrac{\sqrt{3} \cdot (\sqrt{7} + \sqrt{12})}{\sqrt{7^2} - \sqrt{12^2}}$

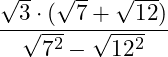
Sowohl der Grad der Wurzeln im Nenner als auch die Exponenten der Radianten weisen den Grad 2 auf, demnach fallen Wurzeln und Exponenten weg:

$\dfrac{\sqrt{3} \cdot (\sqrt{7} + \sqrt{12})}{7 - 12}$

$\dfrac{\sqrt{3} \cdot (\sqrt{7} + \sqrt{12})}{-5}$

$-\dfrac{\sqrt{3} \cdot (\sqrt{7} + \sqrt{12})}{5}$

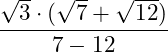
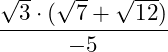
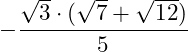
Wir können im Zähler noch die Wurzelgesetze der Multiplikation anwenden:

$-\dfrac{ \sqrt{3 \cdot 7} + \sqrt{3 \cdot 12}}{5}$

$-\dfrac{ \sqrt{21} + \sqrt{36}}{5}$

$-\dfrac{ \sqrt{21} + 6}{5}$

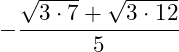
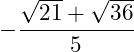
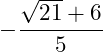
Der Nenner ist rational.

Tipps und Tricks

Konjugierter Ausdruck: Der konjugierte Ausdruck ist entscheidend, um die Wurzeln im Nenner zu beseitigen. Er wird gebildet, indem man das Vorzeichen der Wurzel im Nenner ändert.

Vereinfachen: Nach dem Rationalisieren sollte der Bruch so weit wie möglich vereinfacht werden.

Mögliche Fragestellungen | Häufig gestellte Fragen (FAQs)

1. Warum muss man den Nenner rationalisieren?

Ein rationaler Nenner ist oft leichter zu interpretieren und weiterzuverarbeiten, insbesondere in fortgeschritteneren mathematischen Anwendungen.

2. Was ist der konjugierte Ausdruck?

Der konjugierte Ausdruck eines binomischen Ausdrucks wie $a + b$ ist $a - b$

3. Kann man auch höhere Wurzeln rationalisieren?

Ja, das Prinzip ist ähnlich, aber es erfordert möglicherweise zusätzliche Schritte oder Faktoren, um die höheren Wurzeln zu eliminieren.

Zusammenfassung

Das Rationalisieren des Nenners entfernt Wurzeln aus dem Nenner eines Bruchs, indem der Bruch mit einem geeigneten Ausdruck multipliziert wird. Bei einfachen Wurzeln multipliziert man mit der Wurzel selbst, und bei Ausdrücken mit mehreren Termen verwendet man den konjugierten Ausdruck. Diese Technik erleichtert das Rechnen und vereinfacht viele mathematische Probleme.

Was kommt als Nächstes?

Nachdem du jetzt das Thema Nenner rational machen kennst, behandeln wir in den folgenden Lerneinheiten die Mengenlehre.

Was gibt es noch bei uns?

Optimaler Lernerfolg durch tausende Übungsaufgaben

Übungsbereich (Demo) - Lerne mit mehr als 4000 Übungsaufgaben für deine Prüfungen — Übungsbereich (Demo) – Lerne mit mehr als 4000 Übungsaufgaben für deine Prüfungen

Quizfrage 1

Quizfrage 2

“Wusstest du, dass unter jedem Kursabschnitt eine Vielzahl von verschiedenen interaktiven Übungsaufgaben bereitsteht, mit denen du deinen aktuellen Wissensstand überprüfen kannst?”

Alle Technikerschulen im Überblick

Zum Verzeichnis der Technikerschulen (Alles Rund um die Schulen) — Zum Verzeichnis der Technikerschulen

Kennst du eigentlich schon unser großes Technikerschulen-Verzeichnis für alle Bundesländer mit allen wichtigen Informationen (Studiengänge, Kosten, Anschrift, Routenplaner, Social-Media) ? Nein? – Dann schau einfach mal hinein:

Was ist Technikermathe?

Unser Dozent Jan erklärt es dir in nur 2 Minuten!

Oder direkt den > kostenlosen Probekurs < durchstöbern? – Hier findest du Auszüge aus jedem unserer Kurse!

Geballtes Wissen in derzeit 26 Kursen

Hat dir dieses Thema gefallen? – Ja? – Dann schaue dir auch gleich die anderen Themen zu den Kursen

WT3 (Werkstoffprüfung) und
TM1 (Technische Mechanik – Statik) an.

Lerne nun erfolgreich mit unserem Onlinekurs Technische Mechanik 1 — TM1 (Technische Mechanik)

Lerne nun erfolgreich mit unserem Onlinekurs Werkstofftechnik 3 — WT3 (Werkstoffprüfung)

Perfekte Prüfungsvorbereitung für nur 14,90 EUR/Jahr pro Kurs

++ Günstiger geht’s nicht!! ++

Oder direkt Mitglied werden und Zugriff auf alle 26 Kurse (inkl. Webinare + Unterlagen) sichern ab 7,40 EUR/Monat ++ Besser geht’s nicht!! ++