MA1 – Potenzgesetze [Grundlagen, Erklärungen, Beispiele, Lernclips]

In dieser Lerneinheit behandeln wir die Potenzgesetze.

Für ein optimales Verständnis helfen dir ein Videoclip und mehrere ausführliche Beispiele mit Zahlenwerten zu dem Thema.

Mehr zu diesem Thema und der Mathematik findest du im Kurs: Ma1-Grundlagen der Mathematik

Auch interessant! Alles zu Linearen Gleichungen findest du im Kurs: Ma2-Lineare Gleichungssysteme

Potenzgesetze – Überblick

Mit der Kenntnis der Potenzgesetze wird dir der Umgang mit Potenzen wesentlich einfach fallen und Rechnungen sind plötzlich gar nicht mehr so kompliziert.

Potenzgesetze - Schema — Potenzgesetze – Schema

Wir wollen uns in dieser Lerneinheit mal anschauen, wie die Potenzgesetze aussehen. Dabei unterscheiden wir Potenzen mit gleicher Basis und Potenzen mit unterschiedlicher Basis.

Wir betrachten zunächst Potenzgesetze für Potenzen mit gleicher Basis.

Potenzgesetze: Potenzen mit gleicher Basis

Multiplikation von Potenzen mit gleicher Basis

Multiplizierst du zwei Potenzen mit gleicher Basis a miteinander, so erhältst du das Ergebnis, indem du beide Exponenten miteinander addierst:

$a^n \cdot a^m = a^{n+m}$

Darum geht es

++ Videoclip ++

Im folgenden Video zeigen wir dir, wie du Potenzen mit gleicher Basis multiplizierst!

Beispiel

Betrachten wir dazu ein Beispiel.

Beispiel: Potenzen multiplizieren!

Gegeben sei die Aufgabe:

$x^5 \cdot x^3$

Wie lautet das Ergebnis?

Wir haben hier dieselbe Basis x gegeben. Demnach können wir die beiden Exponenten miteinander addieren:

$x^5 \cdot x^3 = x^{5 + 3} = x^8$

Division von Potenzen mit gleicher Basis

Dividierst du zwei Potenzen mit gleicher Basis, so erhältst du das Ergebnis, indem du die Exponenten der Potenzen voneinander subtrahierst:

$a^n : a^m = a^{n-m}$

bzw.

$\dfrac{a^n}{ a^m} = a^{n-m}$

Beispiel

Betrachten wir dazu ein Beispiel.

Beispiel: Potenzen dividieren!

Gegeben sei:

$\dfrac{x^6}{x^2}$

Wie lautet das Ergebnis?

Wir haben hier dieselbe Basis x gegeben. Demnach können wir die beiden Exponenten voneinander subtrahieren:

$\dfrac{x^6}{x^2} = x^{6 - 2} = x^4$

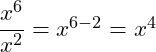
Potenzen potenzieren

Eine Potenz wird potenziert, indem du die beteiligten Exponenten miteinander multiplizierst.

$(a^n)^m = a^{n \cdot m}$

Beispiel

Betrachten wir dazu ein Beispiel.

Beispiel: Potenzen potenzieren!

Gegeben sei:

$(x^4)^3$

Wie lautet das Ergebnis?

Wir haben hier eine Potenz x⁴ gegeben, welche mit 3 potenziert werden soll. Dazu kannst du einfach beide Exponenten miteinander multiplizieren:

$(x^4)^3 = x^{4 \cdot 3} = x^{12}$

Betrachten wir als nächstes Potenzen bei denen die Basis verschieden ist, aber die Exponenten gleich sind.

Potenzgesetze: Potenzen mit gleichen Exponenten

Multiplikation mit unterschiedlicher Basis

Werden zwei Potenzen mit unterschiedlicher Basis aber gleichem Exponenten miteinander multipliziert, kannst du folgendes Potenzgesetz anwenden:

$a^n \cdot b^n = (a \cdot b)^n$

Du kannst also erst die beiden Basen miteinander multiplizieren und das Ergebnis dann Potenzieren. Schauen wir uns dazu mal ein Beispiel an:

Beispiel

Beispiel: Potenz mit gleichen Exponenten!

Gegeben sei:

a) $5^4 \cdot 2^4$

b) $x^3 \cdot y^3$

Wie lautet die Vereinfachung?

Wir haben hier Potenzen mit unterschiedlicher Basis und gleichen Exponenten gegeben. Wir können nun zunächst die Basen miteinander multiplizieren und das Ergebnis dann potenzieren:

a) $5^4 \cdot 2^4 = (5 \cdot 2)^4 = 10^4 = 10.000$

b) $x^3 \cdot y^3 = (x \cdot y)^3$

Division mit unterschiedlicher Basis

Werden zwei Potenzen mit unterschiedlicher Basis aber gleichem Exponenten dividiert, kannst du folgendes Potenzgesetz anwenden:

$a^n : b^n = \dfrac{a^n}{n^n} = (\dfrac{a}{b})^n$

Auch hier bildest du also zunächst das Ergebnis (den Quotienten) und kannst diesen dann potenzieren. Schauen wir uns dazu ein Beispiel an.

Beispiel

Beispiel: Potenz mit gleichen Exponenten!

Gegeben sei:

a) $\dfrac{12^5}{4^5}$

b) $\dfrac{x^7}{y^7}$

Wie lautet die Vereinfachung?

Wir haben hier Potenzen mit unterschiedlicher Basis und gleichen Exponenten gegeben. Wir können nun zunächst die Basen dividieren und das Ergebnis dann potenzieren:

a) 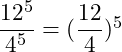$\dfrac{12^5}{4^5} = (\dfrac{12}{4} )^5$

b) 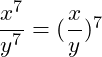$\dfrac{x^7}{y^7} = (\dfrac{x}{y} )^7$

Was kommt als Nächstes?

Nachdem du jetzt alle Potenzgesetze für deine Prüfung kennst, betrachten wir in der nachfolgenden Lerneinheit Wurzeln.

Was gibt es noch bei uns?

Optimaler Lernerfolg durch tausende Übungsaufgaben

Übungsbereich (Demo) - Lerne mit mehr als 4000 Übungsaufgaben für deine Prüfungen — Übungsbereich (Demo) – Lerne mit mehr als 4000 Übungsaufgaben für deine Prüfungen

Quizfrage 1

Quizfrage 2

“Wusstest du, dass unter jedem Kursabschnitt eine Vielzahl von verschiedenen interaktiven Übungsaufgaben bereitsteht, mit denen du deinen aktuellen Wissensstand überprüfen kannst?”

Alle Technikerschulen im Überblick

Zum Verzeichnis der Technikerschulen (Alles Rund um die Schulen) — Zum Verzeichnis der Technikerschulen

Kennst du eigentlich schon unser großes Technikerschulen-Verzeichnis für alle Bundesländer mit allen wichtigen Informationen (Studiengänge, Kosten, Anschrift, Routenplaner, Social-Media) ? Nein? – Dann schau einfach mal hinein:

Was ist Technikermathe?

Unser Dozent Jan erklärt es dir in nur 2 Minuten!

Oder direkt den > kostenlosen Probekurs < durchstöbern? – Hier findest du Auszüge aus jedem unserer Kurse!

Geballtes Wissen in derzeit 26 Kursen

Hat dir dieses Thema gefallen? – Ja? – Dann schaue dir auch gleich die anderen Themen zu den Kursen

WT3 (Werkstoffprüfung) und
TM1 (Technische Mechanik – Statik) an.

Lerne nun erfolgreich mit unserem Onlinekurs Technische Mechanik 1 — TM1 (Technische Mechanik)

Lerne nun erfolgreich mit unserem Onlinekurs Werkstofftechnik 3 — WT3 (Werkstoffprüfung)

Perfekte Prüfungsvorbereitung für nur 14,90 EUR/Jahr pro Kurs

++ Günstiger geht’s nicht!! ++

Oder direkt Mitglied werden und Zugriff auf alle 26 Kurse (inkl. Webinare + Unterlagen) sichern ab 7,40 EUR/Monat ++ Besser geht’s nicht!! ++