MA1 – Potenzen [Grundlagen, Erklärung, Beispiele, Lernclips]

In dieser Lerneinheit behandeln wir die Potenzen.

Für ein optimales Verständnis helfen dir ein Videoclip und mehrere ausführliche Beispiele mit Zahlenwerten zu dem Thema.

Mehr zu diesem Thema und der Mathematik findest du im Kurs: Ma1-Grundlagen der Mathematik

Auch interessant! Alles zu Linearen Gleichungen findest du im Kurs: Ma2-Lineare Gleichungssysteme

Potenzen | Grundlagen

Das Rechnen mit Potenzen ist ein wichtige Bereich in der Mathematik und kann dir helfen umfangreiche Rechnungen vereinfacht und verkürzt darzustellen.

Potenzen, Potenzieren | positive und negative Exponenten

Das Potenzieren ist eine verkürzte Schreibweise für eine sich wiederholende Multiplikation eines Faktors mit sich selbst. Der Potenzwert ist dabei das Ergebnis des Potenzierens.

Das Rechnen mit Potenzen ist ein wichtiger Teil der Mathematik. Eine Potenz besteht aus einer Basis und einem Exponenten.

Was sind Potenzen?

Eine Potenz ist eine Kurzschreibweise für die wiederholte Multiplikation derselben Zahl. Sie besteht aus einer Basis (die Zahl, die multipliziert wird) und einem Exponenten (die Anzahl der Multiplikationen).

Definition – Formel

Potenzen – Formel

Die Potenz $a^n$ bedeutet, dass die Basis a n-mal mit sich selbst multipliziert wird:

$a^n = a \cdot a \cdot a \cdot a ...$ [n-mal]

Beispiel:

$2^3 = 2 \cdot 2 \cdot 2 = 8$

Beim Potenzieren wird ein Faktor wiederholt mit sich selbst multipliziert. Den Faktor bezeichnet man dabei die Basis. Der Exponent gibt dir Auskunft bezüglich der Anzahl an Wiederholungen. In der nächsten Abbildung siehst du die Kennzeichnung noch mal abgebildet.

Potenzen, Potenzieren | Potenz, Potenzwert, Basis - Erklärung — Potenzen, Potenzieren | Potenz, Potenzwert, Basis – Erklärung

Im Folgenden beschäftigen wir uns mit den natürlichen Exponenten und den negativen Exponenten einer Potenz.

Potenzen mit natürlichen Exponenten

Wenn wir von natürlichen Exponenten sprechen, dann sind dies alle natürlichen Zahlen $\mathbb{N}$ , d.h. also alle ganzen positiven Zahlen. Wobei wir die Null auch berücksichtigen.

In der Basis der Potenz steht also eine Zahl $a$ die einen natürlichen Exponenten $n$ aufweist:

$a^{n}$

mit:

$n \in \mathbb{N}^+0$

Wir wollen nun zunächst die Potenz mit dem Exponenten Null definieren. Jede Zahl, die den Exponenten Null aufweist, wird zu Null:

$a^{0} = 1$ Eine Zahl hoch Null ergibt immer Null.

Jede Zahl die den Exponenten Eins aufweist ergibt sich selbst (Basis bleibt Basis):

$a^{1}= a$ Eine Zahl hoch 1 ergibt immer sich selbst.

Nun betrachten wir Exponenten, die größer als 1 sind:

$n > 1$

Wird eine Basis a mit dem Exponenten n > 1 potenziert, so wird die Basis n-mal mit sich selbst multipliziert:

$a^{n} = a \cdot a \cdot a \cdot a...$ n-mal a mit sich selbst multiplizieren

Schauen wir uns dazu mal Beispiele an:

Beispiel: Positiver Exponent, positive Basis!

$a^3 = a \cdot a \cdot a$

$5^4 = 5 \cdot 5 \cdot 5 \cdot 5 = 625$

Ist in der Basis eine negative Zahl gegeben und ein gerader Exponent, so ist die Potenz positiv:

$(-a)^{2n} = a^{2n}$

Schauen wir uns dazu mal ein Beispiel an:

Beispiel: Positiver Exponent, negative Basis!

$(-2)^4 = (-2) \cdot (-2) \cdot (-2) \cdot (-2) = 16$

$(-x)^4 = (-x) \cdot (-x) \cdot (-x) \cdot (-x) = x^4$

Ist in der Basis eine negative Zahl gegeben und ein ungerader Exponent, so ist die Potenz negativ:

$(-a)^{2n+1} = -a^{2n+1}$

Für ein besseres Verständnis schauen wir uns dazu mal ein Beispiel an:

Beispiel: Ungerader Exponent, negative Basis!

$(-2)^3 = (-2) \cdot (-2) \cdot (-2) = -8$

$(-x)^5 = (-x) \cdot (-x) \cdot (-x) \cdot (-x) \cdot (-x) = -x^5$

Potenzen mit negativen Exponenten

Ist eine Potenz mit negativen Exponenten gegeben, dann wird die Basis n-mal durch sich selbst dividiert:

$a^{-n} = 1 : a : a :a :a ....$ n-mal durch a dividieren

Die Zahl $1$ wird $n$ -mal durch die Basis $a$ dividiert. Wir können das ganze auch als Bruch darstellen, dann wird im Nenner die Basis n-mal mit sich selbst multipliziert:

$a^{-n} = \dfrac{1}{a^n} = \dfrac{1}{a \cdot a \cdot a ...}$ mit $a \neq 0$

Für ein besseres Verständnis schauen wir uns dazu mal ein Beispiel an:

Beispiel: Potenz mit negativem Exponenten!

$10^{-3} = \dfrac{1}{10^3} = \dfrac{1}{10 \cdot 10 \cdot 10} = \dfrac{1}{1000}$

In den meisten Fällen ist nicht der negative Exponent gegeben, sondern eine Potenz im Nenner. Später bei den Ableitungen oder bei der Integralrechnung ist es dann sinnvoll die Potenzdarstellung mit negativem Exponenten zu wählen.

Video: Potenzen mit positiven und negativen Exponenten

Im folgenden Video zeigen wir dir nochmal, was du bei Potenzen mit positiven und negativen Exponenten beachten musst.

Lernclip: Potenzen | negative & positive Exponenten

Potenzen mit Exponenten

Beispiele zu Potenzen

Wir wollen uns in den nachfolgenden Beispielen mal Potenzen mit negativen und positiven Exponenten anschauen.

Beispiel 1 : Potenzen mit positiven Exponenten

Aufgabenstellung

Gegeben sind uns die folgenden Potenzen:

a) $(-3)^4$

b) $-6^2$

c) $(-b)^{300}$

Löse diese so weit wie möglich auf!

Lösung

a) Wir haben eine Potenz mit positiven Exponenten gegeben. Die Basis ist a = -3, wobei das Minuszeichen mit potenziert wird, weil die Klammer dieses mit einschließt. Da wir eine gerade Basis gegeben haben, wird aus dem Minuszeichen ein Pluszeichen. Es ergibt sich also:

$(-0,3)^4 = -3 \cdot -3 \cdot -3 \cdot -3 = 81$

b) Bei dieser Potenz ist die Basis a = 6. Das Minuszeichen gehört hier nicht dazu. Demnach bleibt dieses einfach stehen:

$-6^2 = - ( 6 \cdot 6) = -36$

c) Hier ist die Basis a = -b. Das Minuszeichen gehört wieder zur Basis, weil die Klammer es mit einschließt. Aus dem Minuszeichen wird ein Pluszeichen, weil 300 eine gerade Zahl ist:

$(-b)^{300} = b^{300}$

Weiter können wir hier nicht auflösen, weil wir b nicht kennen.

Beispiel 2: Potenzen mit negativen Exponenten

Aufgabenstellung

Uns sind die folgenden Potenzen gegeben:

a) $-2^{-5}$

b) $(-3)^{-3}$

c) $(-x)^{-12}$

Löse diese so weit wie möglich auf!

Lösung

a) Wir haben eine Potenz mit negativem Exponenten gegeben. Die Basis ist a = 2, wobei das Minuszeichen nicht mit potenziert wird. Das Minuszeichen bleibt also einfach stehen. Wir können diese Potenz auch anders darstellen:

$-2^{-5} = -\dfrac{1}{2^5} = -\dfrac{1}{2 \cdot 2 \cdot 2 \cdot 2 \cdot 2} = -\dfrac{1}{32}$

b) Bei dieser Potenz ist die Basis a = -3. Das Minuszeichen muss hier mit potenziert werden. Die Darstellung als Bruch sieht dann wie folgt aus:

$(-3)^{-3} = \dfrac{1}{(-3)^3} = \dfrac{1}{-3 \cdot -3 \cdot -3} = \dfrac{1}{-27} = - \dfrac{1}{27}$

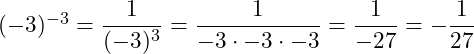
Es verbleibt ein Minuszeichen, weil ein ungerader Exponent gegeben ist.

c) Hier ist die Basis a = -x. Das Minuszeichen gehört wieder zur Basis, weil die Klammer es mit einschließt. Aus dem Minuszeichen wird ein Pluszeichen, weil 12 eine gerade Zahl ist:

$(-x)^{-12} = \dfrac{1}{(-x)^{12}} = \dfrac{1}{x^{12} }$

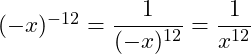
Weiter können wir an dieser Stelle nicht auflösen, weil wir x nicht kennen.

Mögliche Fragestellungen | Häufig gestellte Fragen (FAQs)

1. Was ist eine Potenz?

Eine Potenz ist eine Zahl, die durch wiederholte Multiplikation einer Basis mit sich selbst gebildet wird.

2. Wie multipliziert man Potenzen mit gleicher Basis?

Man addiert die Exponenten.

3. Wie teilt man Potenzen mit gleicher Basis?

Man subtrahiert die Exponenten.

4. Was bedeutet ein negativer Exponent?

Ein negativer Exponent bedeutet die Umkehrung der Basis.

Zusammenfassung

Das Rechnen mit Potenzen ist einfach, wenn man die grundlegenden Potenzgesetze kennt. Diese Gesetze helfen beim Multiplizieren, Dividieren und Potenzieren von Zahlen mit Exponenten. Mit diesen Regeln kannst du schnell und korrekt mit Potenzen arbeiten.

Was kommt als Nächstes?

Nachdem du jetzt einiges über das Thema Potenzen erfahren hast, wollen wir in der nachfolgenden Lerneinheit das Wissen zu diesem Bereiche vertiefen und besprechen die Potenzgesetze.

Was gibt es noch bei uns?

Optimaler Lernerfolg durch tausende Übungsaufgaben

Übungsbereich (Demo) - Lerne mit mehr als 4000 Übungsaufgaben für deine Prüfungen — Übungsbereich (Demo) – Lerne mit mehr als 4000 Übungsaufgaben für deine Prüfungen

Quizfrage 1

Quizfrage 2

“Wusstest du, dass unter jedem Kursabschnitt eine Vielzahl von verschiedenen interaktiven Übungsaufgaben bereitsteht, mit denen du deinen aktuellen Wissensstand überprüfen kannst?”

Alle Technikerschulen im Überblick

Zum Verzeichnis der Technikerschulen (Alles Rund um die Schulen) — Zum Verzeichnis der Technikerschulen

Kennst du eigentlich schon unser großes Technikerschulen-Verzeichnis für alle Bundesländer mit allen wichtigen Informationen (Studiengänge, Kosten, Anschrift, Routenplaner, Social-Media) ? Nein? – Dann schau einfach mal hinein:

Was ist Technikermathe?

Unser Dozent Jan erklärt es dir in nur 2 Minuten!

Oder direkt den > kostenlosen Probekurs < durchstöbern? – Hier findest du Auszüge aus jedem unserer Kurse!

Geballtes Wissen in derzeit 26 Kursen

Hat dir dieses Thema gefallen? – Ja? – Dann schaue dir auch gleich die anderen Themen zu den Kursen

WT3 (Werkstoffprüfung) und
TM1 (Technische Mechanik – Statik) an.

Lerne nun erfolgreich mit unserem Onlinekurs Technische Mechanik 1 — TM1 (Technische Mechanik)

Lerne nun erfolgreich mit unserem Onlinekurs Werkstofftechnik 3 — WT3 (Werkstoffprüfung)

Perfekte Prüfungsvorbereitung für nur 14,90 EUR/Jahr pro Kurs

++ Günstiger geht’s nicht!! ++

Oder direkt Mitglied werden und Zugriff auf alle 26 Kurse (inkl. Webinare + Unterlagen) sichern ab 7,40 EUR/Monat ++ Besser geht’s nicht!! ++