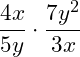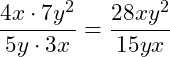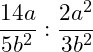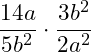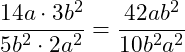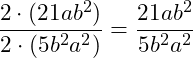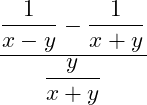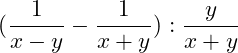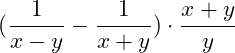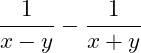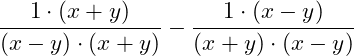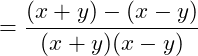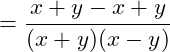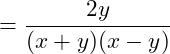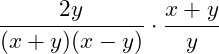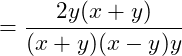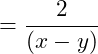MA1 – Brüche multiplizieren | Brüche dividieren [Grundlagen, Erklärung, Beispiele, Lernclips]

In dieser Lerneinheit wollen wir uns anschauen, wie du Brüche multiplizieren und Brüche dividieren kannst.

Für ein optimales Verständnis helfen dir zwei Videoclips und drei ausführliche Beispiele mit Zahlenwerten zu dem Thema.

Mehr zu diesem Thema und der Mathematik findest du im Kurs: Ma1-Grundlagen der Mathematik

Auch interessant! Alles zu Linearen Gleichungen findest du im Kurs: Ma2-Lineare Gleichungssysteme

Brüche multiplizieren und Brüche dividieren

Brüche multiplizieren – Grundlagen

Brüche multiplizieren - Multiplikation von Brüchen - Schema — Brüche multiplizieren – Multiplikation von Brüchen – Schema

Was ist das Multiplizieren von Brüchen?

Beim Multiplizieren von Brüchen werden zwei oder mehr Brüche kombiniert, um ein Produkt zu erhalten. Dabei werden die Zähler (die oberen Zahlen) und die Nenner (die unteren Zahlen) jeweils miteinander multipliziert.

Anleitung | Schritte zum Multiplizieren von Brüchen

Multipliziere die Zähler:
Um das Produkt der Zähler zu erhalten, multipliziere einfach die Zähler der beiden Brüche.

$\frac{a}{b} \cdot \frac{c}{d} = \frac{ a \cdot c}{b \cdot d}$

Beispiel: $\frac{2}{3} \cdot \frac{4}{5} = \frac{ 2 \cdot 4}{3 \cdot 5} = \frac{8}{15}$

Multipliziere die Nenner:
Um den neuen Nenner zu erhalten, multipliziere die Nenner der beiden Brüche.
Beispiel: $\frac{2}{3} \cdot \frac{4}{5} = \frac{8}{15}$

Der Nenner ist 15, da
$3 \cdot 5 = 15$

Kürzen (falls möglich):
Manchmal kann das Ergebnis gekürzt werden. Dies geschieht, indem man den größten gemeinsamen Teiler (ggT) von Zähler und Nenner findet und beide durch diesen teilt.
Beispiel: $\frac{6}{8} = \frac{\frac{6}{2}}{\frac{8}{2}} = \frac{3}{4}$

Tipps und Tricks | Multiplikation von Brüchen

Merk’s dir!

Vor dem Multiplizieren kürzen: Es ist oft einfacher, die Brüche zu kürzen, bevor man sie multipliziert. Das spart Arbeit und vereinfacht die Berechnung.
Ganzzahlige Faktoren: Wenn einer der Faktoren eine ganze Zahl ist, kann er als Bruch mit dem Nenner 1 geschrieben werden.

Beispiel: $3 \cdot \frac{2}{5} = \frac{3}{1} \cdot \frac{2}{5} = \frac{3 \cdot 2}{1 \cdot 5} = \frac{5}{6}$

Mögliche Fragestellungen | Häufig gestellte Fragen (FAQs)

1. Was passiert, wenn einer der Brüche negativ ist?

Die Regel bleibt die gleiche. Achte nur darauf, das Vorzeichen im Zähler oder Nenner zu behalten.
Beispiel:

$\frac{- 2}{3} \cdot \frac{4}{5} = \frac{ - 2 \cdot 4}{3 \cdot 5} = \frac{-8}{15} = - \frac{8}{15}$

2. Kann man gemischte Zahlen multiplizieren?

Ja, aber zuerst sollten sie in unechte Brüche umgewandelt werden.
Beispiel:

$1 \cdot \frac{1}{2} = \frac{3}{2}$

Dann kann man die gewöhnliche Multiplikation von Brüchen anwenden.

Zusammenfassung | Multiplikation von Brüchen

Das Multiplizieren von Brüchen ist einfach, wenn man die Zähler und Nenner separat multipliziert und das Ergebnis kürzt. Mit diesen einfachen Schritten kannst du schnell und korrekt Brüche multiplizieren.

Formel | Brüche multiplizieren

Bei der Multiplikation von zwei Brüchen, also dem Brüche multiplizieren werden die Zähler der beiden Brüchen und die Nenner der beiden Brüche miteinander multipliziert. Es resultiert als Ergebnis ein Bruch.

Multiplikation von Brüchen

$\dfrac{a}{b} \cdot \dfrac{c}{d} = \dfrac{a \cdot c}{b \cdot d}$

Beispiel 1 | Brüche multiplizieren

Schauen wir uns dazu mal ein einfaches Beispiel an:

Beispiel: Zwei Brüche multiplizieren!

$\dfrac{5}{8} \cdot \dfrac{4}{7}$

$\dfrac{5 \cdot 4}{8 \cdot 7} = \dfrac{20}{56}$

Wir können das Ergebnis noch kürzen, indem wir einen gemeinsamen Faktor (hier: 4) ausklammern:

$\dfrac{4 \cdot (5)}{4 \cdot (14)} = \dfrac{5}{14}$

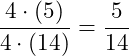
Beispiel 2 | Brüche multiplizieren

Schauen wir uns dazu mal ein weiteres Beispiel an.

Beispiel 2: Brüche multiplizieren!

$\dfrac{4x}{5y} \cdot \dfrac{7y^2}{3x}$

Führe die Multiplikation durch und kürze soweit wie möglich!

Wir multiplizieren zunächst beide Brüche miteinander, indem wir Zähler und Nenner miteinander multiplizieren:

$\dfrac{4x \cdot 7y^2}{5y \cdot 3x} = \dfrac{28xy^2}{15yx}$

Danach können wir gemeinsamen Faktoren kürzen. Betrachten wir zunächst die Zahl im Zähler und Nenner (28 und 15). Hier kann nicht gekürzt werden, da kein gemeinsamer Teiler gegeben ist. Betrachten wir dann die Variablen im Zähler und im Nenner.

Wir haben im Zähler die Variable x und im Nenner die Variable x gegeben. Diese können wir also ausklammern. Außerdem haben wir im Zähler die Variable y² = y ·y und im Nenner y, wir können also y ausklammern. Wir Klammer also xy aus und kürzen:

$\dfrac{xy \cdot (28y}{xy \cdot (15)} = \dfrac{28y}{15}$

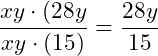
Brüche dividieren – Grundlagen

Brüche dividieren, Division von Brüchen | Schema

Was ist das Dividieren von Brüchen?

Beim Dividieren von Brüchen wird der erste Bruch durch den zweiten Bruch geteilt. Dies geschieht, indem man den ersten Bruch mit dem Kehrwert (reziproken Wert) des zweiten Bruchs multipliziert.

Anleitung | Schritte zum Dividieren von Brüchen

Kehrwert des zweiten Bruchs finden:
Der Kehrwert eines Bruchs wird durch Vertauschen von Zähler und Nenner gebildet.

$\frac{\frac{a}{b}}{\frac{c}{d}} = \frac{a}{b} \cdot \frac{d}{c}$

Beispiel: $\frac{(\frac{2}{3})}{(\frac{4}{5})} = \frac{2}{3} \cdot \frac{5}{4}$

Multipliziere die Zähler:
Multipliziere die Zähler der beiden Brüche.

Beispiel: $\frac{2}{3} \cdot \frac{5}{4} = \frac{ 2 \cdot 5}{3 \cdot 4} = \frac{10}{12}$

Multipliziere die Nenner:

Multipliziere die Nenner der beiden Brüche.

Beispiel: $\frac{2}{3} \cdot \frac{5}{4} = \frac{10}{12}$

Kürzen (falls möglich):
Manchmal kann das Ergebnis gekürzt werden. Dies geschieht, indem man den größten gemeinsamen Teiler (ggT) von Zähler und Nenner findet und beide durch diesen teilt.
Beispiel: $\frac{10}{12} = \frac{(\frac{10}{2})}{(\frac{12}{2})} = \frac{5}{6}$

Tipps und Tricks | Division von Brüchen

Merk’s dir!

Vor dem Dividieren kürzen: Es ist oft einfacher, die Brüche zu kürzen, bevor man sie multipliziert, um die Berechnung zu vereinfachen.
Ganzzahlige Faktoren: Wenn einer der Faktoren eine ganze Zahl ist, kann er als Bruch mit dem Nenner 1 geschrieben werden.

Beispiel: $3 \cdot \frac{2}{5} = \frac{3}{1} \cdot \frac{2}{5} = \frac{3 \cdot 2}{1 \cdot 5} = \frac{5}{6}$

Mögliche Fragestellungen | Häufig gestellte Fragen (FAQs)

1. Was passiert, wenn einer der Brüche negativ ist?

Die Regel bleibt die gleiche. Achte nur darauf, das Vorzeichen im Zähler oder Nenner zu behalten.
Beispiel:

$\frac{(\frac{- 2}{3})}{(\frac{4}{5})} = \frac{- 2}{3} \cdot \frac{5}{4} = \frac{ -2 \cdot 5}{3 \cdot 4} = \frac{-10}{12} = \frac{-5}{6}$

2. Kann man gemischte Zahlen dividieren?

Ja, aber zuerst sollten sie in unechte Brüche umgewandelt werden.
Beispiel:

$1 \cdot \frac{1}{2} = \frac{3}{2}$

Dann kann man die gewöhnliche Division von Brüchen anwenden.

Zusammenfassung | Division von Brüchen

Das Dividieren von Brüchen ist einfach, wenn man den Kehrwert des zweiten Bruchs bildet und dann die Zähler und Nenner multipliziert. Mit diesen einfachen Schritten kannst du schnell und korrekt Brüche dividieren.

Formel | Brüche dividieren

Du kannst zwei Brüche dividieren, indem du den Dividend mit dem Kehrwert des Divisors multiplizierst:

Multiplikation von Brüchen

$\dfrac{a}{b} : \dfrac{c}{d} = \dfrac{a}{b} \cdot \dfrac{d}{c}$

mit

$\dfrac{a}{b}$ Dividend

$\dfrac{c}{d}$ Divisor

Beispiel 1 | Brüche dividieren

Schauen wir uns dazu mal ein einfaches Beispiel an:

Beispiel: Zwei Brüche dividieren!

$\dfrac{7}{8} : \dfrac{6}{5}$

$\dfrac{7}{8} \cdot \dfrac{5}{6}$ Multiplikation mit dem Kehrwert des zweiten Bruchs

$\dfrac{7 \cdot 5}{8 \cdot 6} = \dfrac{35}{48}$

Hier ist kein weiteres Kürzen mehr möglich!

Beispiel 2 | Brüche dividieren

Schauen wir uns dazu mal ein weiteres Beispiel an.

Beispiel: Brüche dividieren!

$\dfrac{14a}{5b^2} : \dfrac{2a^2}{3b^2}$

Führe die Division durch und kürze soweit wie möglich!

Zunächst multiplizieren wir den 1. Bruch mit dem Kehrwert des 2. Bruchs:

$\dfrac{14a}{5b^2} \cdot \dfrac{3b^2}{2a^2}$

$\dfrac{14a \cdot 3b^2}{5b^2 \cdot 2a^2} = \dfrac{42ab^2}{10b^2a^2}$

Danach können wir gemeinsamen Faktoren kürzen. Betrachten wir zunächst die Zahl im Zähler und Nenner (42 und 10). Hier ist der gemeinsame größte Teiler die 2. Ausklammern und kürzen:

$\dfrac{2 \cdot (21ab^2)}{2 \cdot (5b^2a^2)} = \dfrac{21ab^2}{5b^2a^2}$

Betrachten wir als nächstes die Variablen im Zähler und im Nenner. Wir haben im Zähler die Variable a und im Nenner die Variable a² = a · a gegeben. Hier können wir also ein a ausklammern. Außerdem haben wir im Zähler die Variable b² = b · b und im Nenner b² gegeben, wir können also b² ausklammern. Wir Klammer also ab² aus und kürzen:

$\dfrac{ab^2 \cdot (21)}{ab² \cdot (5a)} = \dfrac{21}{5a}$

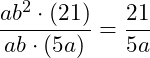
Brüche dividieren: Doppelbruch

Bruch über Bruch - Doppelbruch | Schema — Bruch über Bruch – Doppelbruch | Schema

Der Doppelpunkt als Divisionszeichen kann auch mittels Bruchstrich ausgedrückt werden. Es entsteht dann ein Doppelbruch. Auch hier gelten die Regeln für die Division von Brüchen:

Doppelbruch | Division von Brüchen

$\dfrac{\dfrac{a}{b}}{\dfrac{c}{d}} = \dfrac{a}{b} : \dfrac{c}{d} = \dfrac{a}{b} \cdot \dfrac{d}{c}$

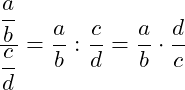
Beispiel: Brüche dividieren – Doppelbruch

Betrachten wir dazu mal ein Beispiel:

Beispiel: Brüche dividieren!

$\dfrac{\dfrac{1}{x-y} - \dfrac{1}{x+y}}{\dfrac{y}{x+y}}$

Zunächst können wir die Division auch mit einem Doppelpunkt darstellen:

$(\dfrac{1}{x-y} - \dfrac{1}{x+y}) : \dfrac{y}{x+y}$

Danach multiplizieren wir mit dem Kehrwert des Bruchs:

$(\dfrac{1}{x-y} - \dfrac{1}{x+y}) \cdot \dfrac{x+y}{y}$

Die Zählerbrüche wollen wir Subtrahieren, dazu benötigen wir den Hauptnenner:

$\dfrac{1}{x-y} - \dfrac{1}{x+y}$

Hauptnenner bilden: $(x-y)(x+y)$

Den 1. Bruchs müssen wir mit (x+y) erweitern, den 2. Bruch mit (x-y):

$\dfrac{1 \cdot (x+y)}{(x-y) \cdot (x+y)} - \dfrac{1 \cdot (x-y)}{(x+y) \cdot (x-y)}$

$= \dfrac{(x+y) - (x-y)}{(x+y)(x-y)}$

$=\dfrac{x+y - x+y}{(x+y)(x-y)}$

$= \dfrac{2y}{(x+y)(x-y)}$

Danach wird der zusammengefasste Zähler mit dem Kehrwert des Nenners multipliziert:

$\dfrac{2y}{(x+y)(x-y)} \cdot \dfrac{x+y}{y}$

$= \dfrac{2y (x+y)}{(x+y)(x-y)y}$

$= \dfrac{2}{ (x-y)}$

Was kommt als Nächstes?

Nachdem du weißt, wie wir Brüche dividieren und Brüche multiplizieren, betrachten wir in der folgenden Lerneinheit die Darstellung eines Bruchs als gemischten Bruch.

Was gibt es noch bei uns?

Optimaler Lernerfolg durch tausende Übungsaufgaben

Übungsbereich (Demo) - Lerne mit mehr als 4000 Übungsaufgaben für deine Prüfungen — Übungsbereich (Demo) – Lerne mit mehr als 4000 Übungsaufgaben für deine Prüfungen

Quizfrage 1

Quizfrage 2

“Wusstest du, dass unter jedem Kursabschnitt eine Vielzahl von verschiedenen interaktiven Übungsaufgaben bereitsteht, mit denen du deinen aktuellen Wissensstand überprüfen kannst?”

Alle Technikerschulen im Überblick

Zum Verzeichnis der Technikerschulen (Alles Rund um die Schulen) — Zum Verzeichnis der Technikerschulen

Kennst du eigentlich schon unser großes Technikerschulen-Verzeichnis für alle Bundesländer mit allen wichtigen Informationen (Studiengänge, Kosten, Anschrift, Routenplaner, Social-Media) ? Nein? – Dann schau einfach mal hinein:

Was ist Technikermathe?

Unser Dozent Jan erklärt es dir in nur 2 Minuten!

Oder direkt den > kostenlosen Probekurs < durchstöbern? – Hier findest du Auszüge aus jedem unserer Kurse!

Geballtes Wissen in derzeit 26 Kursen

Hat dir dieses Thema gefallen? – Ja? – Dann schaue dir auch gleich die anderen Themen zu den Kursen

WT3 (Werkstoffprüfung) und
TM1 (Technische Mechanik – Statik) an.

Lerne nun erfolgreich mit unserem Onlinekurs Technische Mechanik 1 — TM1 (Technische Mechanik)

Lerne nun erfolgreich mit unserem Onlinekurs Werkstofftechnik 3 — WT3 (Werkstoffprüfung)

Perfekte Prüfungsvorbereitung für nur 14,90 EUR/Jahr pro Kurs

++ Günstiger geht’s nicht!! ++

Oder direkt Mitglied werden und Zugriff auf alle 26 Kurse (inkl. Webinare + Unterlagen) sichern ab 7,40 EUR/Monat ++ Besser geht’s nicht!! ++