MA1 – Brüche addieren, Brüche subtrahieren [Grundlagen, Erklärung, Beispiele, Lernclips]

In dieser Lerneinheit zeigen wir dir wie wir Brüche addieren und Brüche subtrahieren und wie der gemeinsame Nenner (Hauptnenner) bestimmt wird.

Für ein optimales Verständnis helfen dir zwei Videoclips und drei ausführliche Beispiele mit Zahlenwerten zu dem Thema.

Mehr zu diesem Thema und der Mathematik findest du im Kurs: Ma1-Grundlagen der Mathematik

Auch interessant! Alles zu Linearen Gleichungen findest du im Kurs: Ma2-Lineare Gleichungssysteme

Brüche addieren und Brüche subtrahieren – Überblick

Wir wollen uns in diesem Lerntext mal ausführlich anschauen, wie wir Brüche addieren und subtrahieren. Dabei wollen wir zwischen gleichnamigen und ungleichnamigen Brüchen unterscheiden. Im ersten Fall ist die Addition bzw. Subtraktion sehr einfach durchzuführen. Im letzteren Fall muss der gemeinsame Nenner der gegebenen Brüche gebildet werden.

Brüche addieren – Grundlagen

Brüche addieren – Erklärung

Das Addieren von Brüchen ist eine grundlegende mathematische Fähigkeit, die Du in vielen schulischen und alltäglichen Situationen gebrauchen kannst. Diese Anleitung erklärt Dir Schritt für Schritt, wie Du Brüche addieren kannst, auch wenn sie unterschiedliche Nenner haben.

Was bedeutet “Brüche addieren”?

Beim Addieren von Brüchen kombinierst Du die Werte der Brüche, um eine Gesamtsumme zu erhalten. Wenn die Brüche denselben Nenner haben, ist der Vorgang einfach. Bei unterschiedlichen Nennern müssen die Brüche zuerst auf einen gemeinsamen Nenner gebracht werden.

Schritt-für-Schritt-Anleitung zum Addieren von Brüchen

1. Brüche mit gleichem Nenner addieren:
Schritt 1: Addiere die Zähler der Brüche.

Schritt 2: Der Nenner bleibt gleich.

Beispiel: $\frac{3}{8} + \frac{2}{8}$
Addiere die Zähler: $3 + 2 = 5$
Der Nenner bleibt $8$
Ergebnis: $\frac{5}{8}$

2. Brüche mit unterschiedlichem Nenner addieren:
Schritt 1: Finde den kleinsten gemeinsamen Nenner (kgV) der Brüche.

Beispiel: Für die Brüche $\frac{2}{3}$ und $\frac{3}{4}$ ist der kleinste gemeinsame Nenner $12$ .

Schritt 2: Erweitere die Brüche so, dass sie den gleichen Nenner haben.
$\frac{2}{3}$ erweitern mit 4: $\frac{2 \cdot 4}{3 \cdot 4} = \frac{8}{12}$
$\frac{3}{4}$ erweitern mit 3: $\frac{3 \cdot 3}{4 \cdot 3} = \frac{9}{12}$

Schritt 3: Addiere die Zähler der erweiterten Brüche.
$\frac{8}{12} + \frac{9}{12}$
Addiere die Zähler: $8 + 9 = 17$

Schritt 4: Der Nenner bleibt gleich.
Ergebnis: $\frac{17}{12}$ oder $1 \frac{5}{12}$ als gemischte Zahl.

Brüche subtrahieren – Grundlagen

Brüche addieren – Erklärung

Das Subtrahieren von Brüchen ist eine wichtige mathematische Fähigkeit, die Du in vielen schulischen und alltäglichen Situationen benötigst. Diese Anleitung erklärt Dir Schritt für Schritt, wie Du Brüche subtrahieren kannst, auch wenn sie unterschiedliche Nenner haben.

“Was bedeutet “Brüche subtrahieren”?

Beim Subtrahieren von Brüchen ziehst Du den Wert des zweiten Bruchs vom Wert des ersten Bruchs ab. Wenn die Brüche denselben Nenner haben, ist der Vorgang einfach. Bei unterschiedlichen Nennern müssen die Brüche zuerst auf einen gemeinsamen Nenner gebracht werden.

Schritt-für-Schritt-Anleitung zum Subtrahieren von Brüchen

1. Brüche mit gleichem Nenner subtrahieren:
Schritt 1: Subtrahiere die Zähler der Brüche.

Schritt 2: Der Nenner bleibt gleich.

Beispiel: $\frac{5}{8} - \frac{3}{8}$
– Subtrahiere die Zähler: $5 - 3 = 2$
– Der Nenner bleibt $8$
– Ergebnis: $\frac{2}{8}$ , was gekürzt $\frac{1}{4}$ ergibt.

2. Brüche mit unterschiedlichem Nenner subtrahieren:
Schritt 1: Finde den kleinsten gemeinsamen Nenner (kgV) der Brüche.

Beispiel: Für die Brüche $\frac{3}{4}$ und $\frac{1}{6}$ ist der kleinste gemeinsame Nenner 12.

Schritt 2: Erweitere die Brüche so, dass sie den gleichen Nenner haben.
$\frac{3}{4}$ erweitern mit 3: $\frac{3 \cdot 3}{4 \cdot 3} = \frac{9}{12}$
$\frac{1}{6}$ erweitern mit 2: $\frac{1 \cdot 2}{6 \cdot 2} = \frac{2}{12}$

Schritt 3: Subtrahiere die Zähler der erweiterten Brüche.
$\frac{9}{12} - \frac{2}{12}$
Subtrahiere die Zähler: $9 - 2 = 7$

Schritt 4: Der Nenner bleibt gleich.
Ergebnis: $\frac{7}{12}$

Schauen wir uns die beiden Möglichkeiten mal im Detail an.

Gleichnamige Brüche addieren und subtrahieren

Von gleichnamigen Brüchen ist die Rede, wenn diese denselben Nennerwert aufweisen, z.B.:

Gleichnamiger Bruch

$\dfrac{a}{b}$ und $\dfrac{c}{b}$

Beide Brüche haben als Nenner b gegeben. Demnach handelt es sich hier um einen gleichnamigen Bruch. Gleichnamige Brüche werden miteinander addiert, indem die Zähler miteinander addiert werden. Der Nenner verändert sich nicht:

Gleichnamiger Bruch – Addition

$\dfrac{a}{b} + \dfrac{c}{b} = \dfrac{a+c}{b}$

Gleichnamige Brüche werden miteinander subtrahiert, indem die Zähler subtrahiert werden. Der Nenner verändert sich nicht:

Gleichnamiger Bruch – Subtraktion

$\dfrac{a}{b} - \dfrac{c}{b} = \dfrac{a-c}{b}$

Schauen wir uns dazu mal ein Beispiel an:

Beispiel: Gleichnamige Brüche!

$\dfrac{1}{5} + \dfrac{3}{5} = \dfrac{1 + 3}{5} = \dfrac{4}{5}$

Ungleichnamige Brüche addieren und subtrahieren

Ungleichnamige Brüche addieren - Schema | Formel — Ungleichnamige Brüche addieren – Schema | Formel

Ungleichnamige Brüche sind Brüche, die nicht denselben Nennerwert aufweisen:

Ungleichnamiger Bruch

$\dfrac{a}{b}$ und $\dfrac{c}{d}$

Ungleichnamige Brüche werden addiert bzw. subtrahiert, indem man die Einzelbrüche auf einen gemeinsamen Nenner, den Hauptnenner, erweitert und dann die Zähler addiert bzw. subtrahiert. Der Hauptnenner ist das kleinste gemeinsame Vielfache der Einzelnenner:

Ungleichnamig Brüche addieren/subtrahieren

$\dfrac{a}{b} \pm \dfrac{c}{d} = \dfrac{a \cdot d \pm c \cdot b}{b \cdot d}$

Schauen wir uns dazu ein Beispiel an:

Beispiel: Ungleichnamige Brüche addieren!

$\dfrac{1}{7} + \dfrac{2}{3}$

Führe die Addition durch!

Wir suchen für den gemeinsamen Nenner (Hauptnenner) das kleinste gemeinsame Vielfache. Also diejenige Zahl, durch welche sowohl 7 als auch 3 teilbar sind.

Das kleinste Vielfache ist hierbei $3 \cdot 7 = 21$ . Denn 21 ist sowohl durch 7 also auch durch 3 teilbar. Unser Ziel ist also, den Hauptnenner 21 zu erreichen. Dazu müssen wir den 1. Bruch mit 3 erweitern und den 2. Bruch mit 7 erweitern. Erweitern bedeutet, dass wir sowohl Zähler als auch Nenner mit derselben Zahl multiplizieren:

$\dfrac{1}{7} + \dfrac{2}{3} = \dfrac{1 \cdot 3}{6 \cdot 3} + \dfrac{2 \cdot 7}{3 \cdot 7} = \dfrac{3}{21} + \dfrac{14}{21} = \dfrac{17}{21}$

Lernclips: Brüche addieren und subtrahieren

In den folgenden Videos behandeln wir die Addition und Subtraktion von gleichnamigen und ungleichnamigen Brüchen.

Lernclip: Brüche addieren und subtrahieren

Brüche addieren und subtrahieren

Videoclip 1: Addition gleichnamiger und ungleichnamiger Brüche

Videoclip 2: Addition ungleichnamiger Brüche

Brüche addieren und subtrahieren

Wir wollen uns in den folgenden Beispielen lernen, wie wir Brüche addieren und subtrahieren. Du solltest diese Berechnungen in jedem Fall üben, denn sie werden dir später bei der Zusammenfassung von Bruchgleichungen wieder begegnen.

Beispiel 1 : Brüche subtrahieren

Aufgabenstellung

$\dfrac{3x}{x + y} - 2$

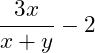
Führe die Subtraktion durch!

Lösung

Wir können auch schreiben:

$\dfrac{3x}{x + y} - \dfrac{2}{1}$

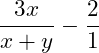
Hauptnenner bilden:

$(x + y) \cdot 1$

Wir müssen also den 1. Bruch mit 1 erweitern und den 2. Bruch mit $(x + y)$ :

$\dfrac{3x \cdot 1}{(x + y) \cdot 1} - \dfrac{2 \cdot \(x + y)}{1 \cdot \(x + y)}$

$\dfrac{3x }{x + y} - \dfrac{2 (x + y)}{x + y} =\dfrac{3x}{x + y} - \dfrac{2 x + 2y}{x + y}$

$\dfrac{3x - (2x + 2y)}{x + y} = \dfrac{3x - 2x - 2y}{x + y} = \dfrac{x - 2y}{x + y}$

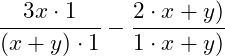
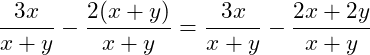
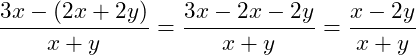
Beispiel 2: Brüche subtrahieren

Aufgabenstellung

$\dfrac{r + 1}{r-1} - 1$

Führe die Subtraktion durch!

Lösung

Wir können auch schreiben:

$\dfrac{r + 1}{r-1} - \dfrac{1}{1}$

Hauptnenner bilden:

$(r-1) \cdot 1$

Wir erweitern den 1. Bruch mit $1$ und den zweiten Bruch mit $(r-1)$ :

$\dfrac{(r + 1) \cdot 1}{(r-1) \cdot 1} - \dfrac{1 \cdot (r-1)}{1 \cdot (r-1)}$

$\dfrac{r + 1}{r-1 } - \dfrac{r-1}{r-1} = \dfrac{r + 1 - (r-1) }{r-1 } = \dfrac{r + 1 - r + 1 }{r-1 } = \dfrac{2}{r-1}$

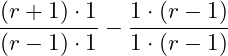
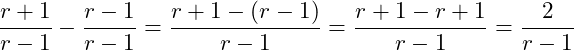
Beispiel 3: Brüche addieren

Aufgabenstellung

$\dfrac{6x }{7x + 14} + \dfrac{12}{7x + 14}$

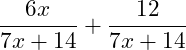
Führe die Addition durch!

Lösung

Wir haben hier bereits beide Nenner gleichnamig:

$\dfrac{6x + 12}{7x + 14}$

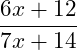
Wir können nun noch 6 im Zähler und 7 im Nenner ausklammern und erhalten:

$\dfrac{6(x + 2)}{7(x + 2)} = \dfrac{6}{7}$

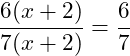
Ergänzende Informationen zum Brüche addieren und subtrahieren

Tipps und Tricks

Überprüfe Deine Arbeit: Stelle sicher, dass die Brüche korrekt erweitert wurden, indem Du den Nenner nach der Erweiterung überprüfst.
Vereinfache das Ergebnis: Wenn möglich, kürze den resultierenden Bruch.
Übe regelmäßig: Je mehr Du Brüche addierst / subtrahierst, desto schneller und sicherer wirst Du.

Fazit

Das Addieren und Subtrahieren von Brüchen ist eine wichtige mathematische Fähigkeit, die Du mit etwas Übung leicht beherrschen kannst. Mit dieser schrittweisen Anleitung kannst Du Brüche sicher und korrekt addieren oder subtrahieren, egal ob sie denselben oder unterschiedliche Nenner haben.

Was kommt als Nächstes?

In der folgenden Lerneinheit behandeln wir die Multiplikation und Division von Brüchen.

Was gibt es noch bei uns?

Optimaler Lernerfolg durch tausende Übungsaufgaben

Übungsbereich (Demo) - Lerne mit mehr als 4000 Übungsaufgaben für deine Prüfungen — Übungsbereich (Demo) – Lerne mit mehr als 4000 Übungsaufgaben für deine Prüfungen

Quizfrage 1

Quizfrage 2

“Wusstest du, dass unter jedem Kursabschnitt eine Vielzahl von verschiedenen interaktiven Übungsaufgaben bereitsteht, mit denen du deinen aktuellen Wissensstand überprüfen kannst?”

Alle Technikerschulen im Überblick

Zum Verzeichnis der Technikerschulen (Alles Rund um die Schulen) — Zum Verzeichnis der Technikerschulen

Kennst du eigentlich schon unser großes Technikerschulen-Verzeichnis für alle Bundesländer mit allen wichtigen Informationen (Studiengänge, Kosten, Anschrift, Routenplaner, Social-Media) ? Nein? – Dann schau einfach mal hinein:

Was ist Technikermathe?

Unser Dozent Jan erklärt es dir in nur 2 Minuten!

Oder direkt den > kostenlosen Probekurs < durchstöbern? – Hier findest du Auszüge aus jedem unserer Kurse!

Geballtes Wissen in derzeit 26 Kursen

Hat dir dieses Thema gefallen? – Ja? – Dann schaue dir auch gleich die anderen Themen zu den Kursen

WT3 (Werkstoffprüfung) und
TM1 (Technische Mechanik – Statik) an.

Lerne nun erfolgreich mit unserem Onlinekurs Technische Mechanik 1 — TM1 (Technische Mechanik)

Lerne nun erfolgreich mit unserem Onlinekurs Werkstofftechnik 3 — WT3 (Werkstoffprüfung)

Perfekte Prüfungsvorbereitung für nur 14,90 EUR/Jahr pro Kurs

++ Günstiger geht’s nicht!! ++

Oder direkt Mitglied werden und Zugriff auf alle 26 Kurse (inkl. Webinare + Unterlagen) sichern ab 7,40 EUR/Monat ++ Besser geht’s nicht!! ++