In dieser Lerneinheit betrachten wir die Themen Brüche kürzen und Brüche erweitern.
Für ein optimales Verständnis helfen dir ein Videoclip und drei ausführliche Beispiele mit Zahlenwerten zu dem Thema. Mehr zu diesem Thema Brüche kürzen und Brüche erweitern sowie der Mathematik findest du im Kurs: Ma1-Grundlagen der Mathematik Auch interessant! Alles zu Linearen Gleichungen findest du im Kurs: Ma2-Lineare Gleichungssysteme
Brüche kürzen | Brüche erweitern – Überblick

Das Kürzen und Erweitern von Brüchen ist bei mathematischen Berechnungen gerade dann notwendig, wenn Gleichungen zusammengefasst oder nach einer Variable aufgelöst werden sollen. Wir schauen uns deswegen an, wie du Brüche erweiterst und kürzt.
Brüche kürzen | Erklärung und Formel

Das Kürzen von Brüchen ist eine grundlegende mathematische Fähigkeit, die häufig in der Schule und im Alltag angewendet wird. Ein gekürzter Bruch ist einfacher zu verstehen und zu verwenden. In dieser Anleitung zeigen wir Ihnen, wie Sie Brüche schnell und einfach kürzen können.
Was bedeutet “Brüche kürzen”?
Das Kürzen eines Bruchs bedeutet, dass man den Zähler (die obere Zahl) und den Nenner (die untere Zahl) durch ihre gemeinsamen Teiler dividiert, um den Bruch zu vereinfachen. Das Ziel ist es, den Bruch auf seine kleinste Form zu bringen.
Faktoren kürzen | Formel
Beim Kürzen eines Bruchs werden Zähler und Nenner durch einen gemeinsamen Faktor dividiert. Der Wert des Bruchs wird dabei nicht verändert.
![]() Kürzen eines Faktors a
Kürzen eines Faktors a
mit ![]()
Summen kürzen und Differenzen kürzen
Bei dem Kürzen von Summen bzw. Differenzen muss immer erst jedes Produkt betrachtet werden und dann der gemeinsame Faktor ausgeklammert werden.
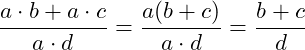
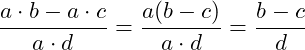
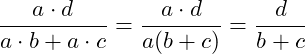
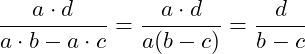
Beim Kürzen müssen Zähler und Nenner als Produkt vorliegen.
Schritt-für-Schritt-Anleitung zum Kürzen von Brüchen
1. Bestimme den größten gemeinsamen Teiler (ggT):
Finde die größten gemeinsamen Teiler (ggT) von Zähler und Nenner. Der ggT ist die größte Zahl, die sowohl den Zähler als auch den Nenner ohne Rest teilt.
Beispiel: Für den Bruch 8/12, die gemeinsamen Teiler von 8 und 12 sind 1, 2 und 4. Der größte gemeinsame Teiler ist 4.
2. Teile Zähler und Nenner durch den ggT:
Dividiere den Zähler und den Nenner des Bruchs durch den ggT.
Beispiel: Teilen Sie 8 und 12 jeweils durch 4. Das ergibt 2/3.
3. Prüfe das Ergebnis:
Stelle sicher, dass der Bruch in seiner einfachsten Form vorliegt. Es sollten keine gemeinsamen Teiler außer 1 zwischen dem Zähler und dem Nenner mehr vorhanden sein.
Beispiel: 2 und 3 haben keine gemeinsamen Teiler außer 1, daher ist 2/3 die gekürzte Form von 8/12.
Beispiele (1-2) | Brüche kürzen
Nun folgen zwei passende Beispiele für ein besseres Verständnis.
Beispiel 1: Brüche kürzen
Schauen wir uns dazu mal ein Beispiel an.
Gegeben seien die beiden Brüche:
a) 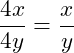
b) 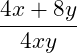
Kürze diese so weit wie möglich!
a) Hier können wir direkt sehen, dass Zähler und Nenner den gemeinsamen Faktor 4 aufweisen und diesen kürzen:
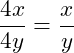
b) Bei diesem Bruch haben wir im Zähler zwei Produkte gegeben (4x und 6y). Wir können hier nicht einfach die 4 vom linken Produkt des Zählers (4x) mit der 4 im Nenner kürzen. Wir müssen immer alle Produkte betrachten. Wie können wir also das Produkt 8y mitberücksichtigen? Hier können wir ganz einfach 4 ausklammern, denn 4 · 2 = 8. Wir können also die 4 oben ausklammern und dann kürzen:
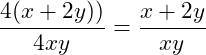
Beispiel 2: Brüche kürzen
Betrachten wir ein weiteres Beispiel.
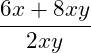
Kürze den Bruch so weit wie mögliche!
Der obige Bruch weist im Zähler zwei Produkte und im Nenner ein Produkt auf. Wir müssen hier zunächst für alle Produkte den gemeinsamen Faktor finden, den wir kürzen können. 2 ist die kleinste zu berücksichtigende Zahl (im Nenner), demnach orientieren wir uns an dieser. Die 2 ist durch 2 teilbar. Wir schauen also, ob wir die 2 im Zähler ausklammern können. Dies ist möglich, da 6/2 = 3 und 8/2 = 4:
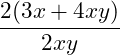
Wir können also die 2 kürzen:
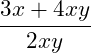
Schauen wir uns den Bruch genauer an, können wir zusätzlich noch die Variable x kürzen, da diese in jedem Produkt vorkommt:
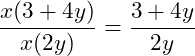
Ergänzende Informationen
Tipps und Tricks
- Wenn der Zähler und der Nenner keine gemeinsamen Teiler außer 1 haben, ist der Bruch bereits in seiner einfachsten Form.
- Verwenden Sie die Primfaktorzerlegung, um den ggT zu finden, falls die Zahlen groß sind.
- Übung macht den Meister – je mehr Brüche Sie kürzen, desto schneller und sicherer werden Sie darin.
Fazit
Das Kürzen von Brüchen ist eine wertvolle Fähigkeit, die das Verständnis und die Anwendung von Brüchen erleichtert. Mit der obigen Anleitung und regelmäßiger Übung können Sie schnell und effizient Brüche kürzen und somit mathematische Aufgaben einfacher bewältigen.
Videoclip: Kürzen von Brüchen
Schauen wir uns das Kürzen von Brüchen mal an einem Beispiel im folgenden Video an:
Brüche erweitern | Erklärung und Formel

Das Erweitern von Brüchen ist eine grundlegende mathematische Technik, die es ermöglicht, Brüche mit einem bestimmten Nenner zu erstellen oder Brüche zu vergleichen. Diese Fähigkeit ist besonders nützlich bei der Addition, Subtraktion und dem Vergleich von Brüchen. In dieser Anleitung erklären wir Ihnen, wie Sie Brüche korrekt erweitern.
Was bedeutet “Brüche erweitern”?
Das Erweitern eines Bruchs bedeutet, dass man sowohl den Zähler (die obere Zahl) als auch den Nenner (die untere Zahl) eines Bruchs mit derselben Zahl multipliziert. Das Ergebnis ist ein Bruch, der denselben Wert hat wie der ursprüngliche, aber einen größeren Nenner und Zähler.
Beim Erweitern von Brüchen werden Zähler und Nenner mit demselben Faktor multipliziert. Der Wert des Bruchs wird dabei nicht verändert.
![]()
mit
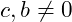
Bei Erweitern von Brüchen muss jedes Produkt mit demselben Faktor multipliziert werden.
Schritt-für-Schritt-Anleitung zum Erweitern von Brüchen
1. Wähle eine Zahl zum Erweitern:
Diese Zahl wird sowohl den Zähler als auch den Nenner multiplizieren. Sie wird als Erweiterungszahl bezeichnet.
Beispiel: Um den Bruch 2/3 zu erweitern, wählen wir die Zahl 4.
2. Multipliziere den Zähler und den Nenner mit der Erweiterungszahl:
Multipliziere den Zähler des Bruchs mit der gewählten Zahl.
Multiplizier den Nenner des Bruchs mit der gleichen Zahl.
Beispiel: 2/3 erweitert mit 4:
Zähler: 2 × 4 = 8
Nenner: 3 × 4 = 12
3. Schreibe den erweiterten Bruch auf:
Der neue Bruch hat den erweiterten Zähler und Nenner.
Beispiel: Der erweiterte Bruch von 2/3 mit der Zahl 4 ist 8/12.
Brüche erweitern | Beispiel
Schauen wir uns dazu ein Beispiel an:
Gegeben seien die folgenden Brüche:
a) ![]()
b) 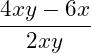
c) 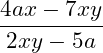
Erweitere beide Brüche mit 5!
a) Gegeben ist ein Bruch mit jeweils einem Produkt im Zähler und einem Produkt im Nenner. Wir können also den Bruch erweitern, indem wir beide Produkte erweitern:
![]()
b) Bei diesem Bruch sind im Zähler zwei Produkte gegeben und im Nenner ein Produkt. Wir müssen nun alle Produkte mit 5 multiplizieren, um den Bruch zu erweitern:
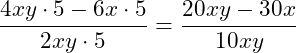
c) Bei diesem Bruch haben wir jeweils zwei Produkte in Nenner und Zähler. Wir müssen nun alle 4 Produkte mit 5 multiplizieren:
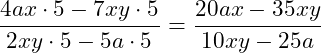
Ergänzende Informationen
Wann sollte man Brüche erweitern?
- Bei der Addition und Subtraktion von Brüchen: Um Brüche mit unterschiedlichen Nennern auf einen gemeinsamen Nenner zu bringen.
- Beim Vergleichen von Brüchen: Um Brüche auf denselben Nenner zu bringen, damit sie leichter verglichen werden können.
- Bei der Umwandlung von Brüchen: Um Brüche in eine gewünschte Form zu bringen, zum Beispiel in Dezimalbrüche.
Tipps und Tricks
- Wählen Sie die kleinste mögliche Erweiterungszahl, um unnötig große Zahlen zu vermeiden.
- Überprüfen Sie Ihre Arbeit, indem Sie den erweiterten Bruch wieder kürzen und sicherstellen, dass er zum ursprünglichen Bruch zurückführt.
- Üben Sie mit verschiedenen Zahlen, um sicherer im Erweitern von Brüchen zu werden.
Fazit
Das Erweitern von Brüchen ist eine einfache, aber wichtige mathematische Technik, die in vielen Situationen nützlich ist. Mit dieser schrittweisen Anleitung und regelmäßiger Übung können Sie Brüche schnell und effizient erweitern, um mathematische Probleme leichter zu lösen.
Das Kürzen und Erweitern von Brüchen wird dir in den nachfolgenden Lerneinheiten noch beim Rechnen mit Brüchen begegnen. Schauen wir uns zunächst mal an, wie Brüche addiert und subtrahiert werden. Anschließend betrachten wir deren Multiplikation und Division.
Was gibt es noch bei uns?
Optimaler Lernerfolg durch tausende Übungsaufgaben

Quizfrage 1
Quizfrage 2
“Wusstest du, dass unter jedem Kursabschnitt eine Vielzahl von verschiedenen interaktiven Übungsaufgaben bereitsteht, mit denen du deinen aktuellen Wissensstand überprüfen kannst?”
Was ist Technikermathe?
Unser Dozent Jan erklärt es dir in nur 2 Minuten!
Oder direkt den > kostenlosen Probekurs < durchstöbern? – Hier findest du Auszüge aus jedem unserer Kurse!
Geballtes Wissen in derzeit 26 Kursen
Hat dir dieses Thema gefallen? – Ja? – Dann schaue dir auch gleich die anderen Themen zu den Kursen
WT3 (Werkstoffprüfung) und
TM1 (Technische Mechanik – Statik) an.


Perfekte Prüfungsvorbereitung für nur 14,90 EUR/Jahr pro Kurs
++ Günstiger geht’s nicht!! ++
Oder direkt Mitglied werden und Zugriff auf alle 26 Kurse (inkl. Webinare + Unterlagen) sichern ab 7,40 EUR/Monat ++ Besser geht’s nicht!! ++
Social Media? - Sind wir dabei!
Dein Technikermathe.de-Team






