(ENT2 15) – Kapitalwertmethode | Barwertmethode [Grundlagen, Formeln, Beispiele]

Nachdem wir schon ein Wenig über die Investitionsrechnung erlernt haben, möchten wir dir als angehenden Techniker mit der Kapitalwertmethode und der Barwertmethode zwei mathematische Verfahren aus diesem Bereich vorstellen.

Für ein optimales Verständnis helfen dir zahlreiche, ausführliche Videoclips und viele anschauliche Rechenbeispiele zu dem Thema.

Mehr zu diesem Thema und der Energietechnik findest du im Kurs: ENT2-Kraftwerkstechnik

Kapitalwertmethode – Grundlagen

Merk’s dir!

“Beide statischen Verfahren dienen in der Energiewirtschaft als Werkzeug um eine Investition auf Substanz zu prüfen.”

Kapitalwertmethode und Barwertmethode - statische Investitionsrechnung — Kapitalwertmethode und Barwertmethode – statische Investitionsrechnung

Worum geht’s eigentlich?…

Mit der Kapitalwertmethode berechnet man den Kapitalwert. Dieser Wert gibt die Höhe des Betrags an den der Investor über die gewünschte Verzinsung des Kapitals hinaus erzielt in Bezug auf den Zahlungszeitpunkt.

Einfach ausgedrückt:

Die Kapitalwertmethode ist eine Möglichkeit, zu prüfen, ob ein Projekt Geld verdient. Man nimmt die erwarteten Einnahmen und Ausgaben des Projekts über die Zeit und berechnet, wie viel sie in der Zukunft wert sind, wenn man sie heute betrachtet.

Wenn der Wert größer ist als die anfänglichen Kosten des Projekts, ist es wahrscheinlich eine gute Investition.

In der Energiewirtschaft kann dies bedeuten, dass eine Investition in etwas wie ein Windkraftwerk oder eine Solaranlage wirtschaftlich ist, wenn die zukünftigen Einnahmen aus dem Stromverkauf die Kosten für den Bau und Betrieb des Projekts übersteigen.

Wir betrachten die Gesamtlaufzeit der Investition. Dabei machen wir sie durch Abzinsung und Aufzinsung der Differenzen von jährlichen Erlöse sowie Aufwendungen zu einem festgelegten Zeitpunkt vergleichbar.

Kapitalwert berechnen

Für jährlich gleichbleibende Einzahlungsüberschüsse ist der Kapitalwert:

$C = (e - a) \frac{(1 + i)^n - 1 }{ i (1 + i)^n} + R_n \frac{1}{(1 + i)^n} - A_0$

Für jährlich unterschiedliche Einzahlungsüberschüsse ist der Kapitalwert:

$C = \sum_{t =1}^{n} \frac{e_t - a_t}{(1 + i)^t} + R_n \frac{1}{(1+i)^n} - A_0$

Kennzahlen:

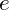$e$ = Einzahlung

sowie

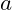$a$ = Auszahlung

sowie

$A_0$ = Anfangsinvestition

sowie

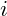$i$ = Zinssatz

sowie

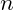$n$ = Nutzungsdauer

und

$R_n$ = Restwert

Barwertfaktor

Der Barwertfaktor ist der Kehrwert des Kapitalwiedergewinnungsfaktors und wird formal beschrieben durch:

$\frac{(1 + i)^n - 1}{i (1 + i)^n}$

Wie so oft in der Mathematik üblich, können wir auch hier drei mögliche Zustände näher beschreiben:

Beispiel – Entscheidungskriterien!

$\text{Kapitalwert: } C > 0 \rightarrow$ Investition durchführen – profitabel – denn die notwendige Verzinsung des eingesetzten Kapitals wird übertroffen.

sowie

$\text{Kapitalwert: }C = 0 \rightarrow$ Investition durchführen – denn die notwendige Verzinsung des eingesetzten Kapitals wird erreicht.

sowie

$\text{Kapitalwert: }C < 0 \rightarrow$ Investition nicht durchführen – nicht profitabel – denn die notwendige Verzinsung des eingesetzten Kapitals wird verfehlt.

Rechenbeispiel – Investitionsrechnung für einen Solarpark

Angenommen, ein Energieunternehmen plant den Bau eines Solarparks. Die Gesamtkosten für den Bau und die Inbetriebnahme des Solarparks belaufen sich auf 1.000.000 Euro. Die erwarteten jährlichen Einnahmen aus dem Verkauf des erzeugten Stroms betragen 200.000 Euro, und die erwarteten jährlichen Betriebskosten werden auf 50.000 Euro geschätzt. Der relevante Diskontsatz beträgt 5%.

Um den Kapitalwert zu berechnen, werden die zukünftigen Cashflows auf ihren Barwert abgezinst und dann die Gesamtkosten abgezogen.

Jahresüberschuss: Jährliche Einnahmen: 200.000 Euro Jährliche Betriebskosten: -50.000 Euro

Netto-Cashflow pro Jahr: 200.000 Euro – 50.000 Euro = 150.000 Euro

Kapitalwertberechnung: Kapitalwert = Σ (Netto-Cashflow / (1 + Diskontsatz)^Jahr) = (150.000 / (1 + 0,05)^1) + (150.000 / (1 + 0,05)^2) + … + (150.000 / (1 + 0,05)^n) – 1.000.000

Angenommen, die Nutzungsdauer des Solarparks beträgt 10 Jahre.

Kapitalwert = (150.000 / 1,05^1) + (150.000 / 1,05^2) + … + (150.000 / 1,05^10) – 1.000.000

Berechnen der Werte: Kapitalwert = (150.000 / 1,05) + (150.000 / 1,05^2) + … + (150.000 / 1,05^10) – 1.000.000

Kapitalwert = 142.857,14 + 136.054,42 + … + 78.663,45 – 1.000.000

Kapitalwert = 108.345,60

Der Kapitalwert des Solarparks beträgt also 108.345,60 Euro. Da dieser Wert positiv ist, würde das Projekt unter Berücksichtigung des Diskontsatzes von 5% voraussichtlich rentabel sein.

Was kommt als Nächstes?

Jetzt kennst du die Kapitalwertmethode und die Barwertmethode, sowie deren Sinn und Zweck bei Investitionsentscheidungen. Im kommenden Kursabschnitt untersuchen wir die dynamische Investitionsrechnung mit der Methode des internen Zinsfußes.

Was gibt es noch bei uns?

Optimaler Lernerfolg durch tausende Übungsaufgaben

Übungsbereich (Demo) - Lerne mit mehr als 4000 Übungsaufgaben für deine Prüfungen — Übungsbereich (Demo) – Lerne mit mehr als 4000 Übungsaufgaben für deine Prüfungen

Quizfrage 1

Quizfrage 2

“Wusstest du, dass unter jedem Kursabschnitt eine Vielzahl von verschiedenen interaktiven Übungsaufgaben bereitsteht, mit denen du deinen aktuellen Wissensstand überprüfen kannst?”

Alle Technikerschulen im Überblick

Zum Verzeichnis der Technikerschulen (Alles Rund um die Schulen) — Zum Verzeichnis der Technikerschulen

Kennst du eigentlich schon unser großes Technikerschulen-Verzeichnis für alle Bundesländer mit allen wichtigen Informationen (Studiengänge, Kosten, Anschrift, Routenplaner, Social-Media) ? Nein? – Dann schau einfach mal hinein:

Was ist Technikermathe?

Unser Dozent Jan erklärt es dir in nur 2 Minuten!

Oder direkt den > kostenlosen Probekurs < durchstöbern? – Hier findest du Auszüge aus jedem unserer Kurse!

Geballtes Wissen in derzeit 26 Kursen

Hat dir dieses Thema gefallen? – Ja? – Dann schaue dir auch gleich die anderen Themen zu den Kursen

WT3 (Werkstoffprüfung) und
TM1 (Technische Mechanik – Statik) an.

Lerne nun erfolgreich mit unserem Onlinekurs Technische Mechanik 1 — TM1 (Technische Mechanik)

Lerne nun erfolgreich mit unserem Onlinekurs Werkstofftechnik 3 — WT3 (Werkstoffprüfung)

Perfekte Prüfungsvorbereitung für nur 14,90 EUR/Jahr pro Kurs

++ Günstiger geht’s nicht!! ++

Oder direkt Mitglied werden und Zugriff auf alle 26 Kurse (inkl. Webinare – Gemeinsames Lernen + Unterlagen) sichern ab 7,40 EUR/Monat ++ Besser geht’s nicht!! ++