Aufgabe: Zustandsgleichung des idealen Gases

Zustandsgleichung idealer Gase?

Vorgehensweise und Beispiel mit schrittweiser Lösung.
Auszug aus unserem Onlinekurs PH5-Wärmelehre.

Wir schauen uns in diesem Beitrag an, wie die Zustandsgleichung für ideale Gase angewendet wird.

Der Zustand eines Gases wird allgemein durch die drei Größen Druck p, Volumen V und Temperatur T beschrieben. Diese drei Größen werden deshalb auch als Zustandsgrößen bezeichnet.

Ändern sich Druck, Volumen und Temperatur gleichzeitig, so kann die Zustandsgleichung des idealen Gases herangezogen werden. Diese Gleichung gilt exakt nur für ideale Gase, weshalb sie auch als Zustandsgleichung der idealen Gase bezeichnet wird.

Ideale Gase kommen in der Realität nicht vor, sondern dienen lediglich der Vereinfachung von Berechnungen. Es gibt aber reale Gase, die unter bestimmten Bedingungen näherungsweise als ideale Gase behandelt werden können.

Merk’s dir!

Viele reale Gase verhalten sich bei Zimmertemperatur t = 17°C – 22°C und geringem Druck näherungsweise wie ideale Gase.

Aufgabe 1: Masse von Sauerstoff berechnen

Ein Behälter mit Sauerstoff hat ein Volumen von 0,15m³ und einen Druck von 18 MPa. Die Temperatur beträgt t = 22°C. Der Sauerstoff soll näherungsweise als ideales Gas angenommen werden.

Berechne die Masse des Sauerstoffs!

Gegeben:

$p = 18 MPa = 18.000.000 Pa$

$V = 0,15m^3$

$T = 22 + 273,15 K = 295,15 K$

Gesucht:

Masse m [kg]

Wir können hier die Masse berechnen, indem wir die Zustandsgleichung für ideale Gase heranziehen:

$p \cdot V = m \cdot R_i \cdot T$

Wir wählen die Zustandsgleichung, in welcher die Masse m vorkommt, da wir diese berechnen sollen. Wir lösen die Zustandsgleichung nach der Masse m auf:

$m = \frac{p \cdot V}{R_i \cdot T}$

In der Aufgabenstellung haben wir den Druck p, das Volumen V sowie die Temperatur T gegeben. Uns fehlt aber die Angabe der spezifischen Gaskonstante R_i. Wir haben aber innerhalb der Aufgabenstellung die Information, dass der Behälter mit Sauerstoff [O₂] gefüllt ist. Wir ziehen das Periodensystem heran und lesen hier die Atommasse ab:

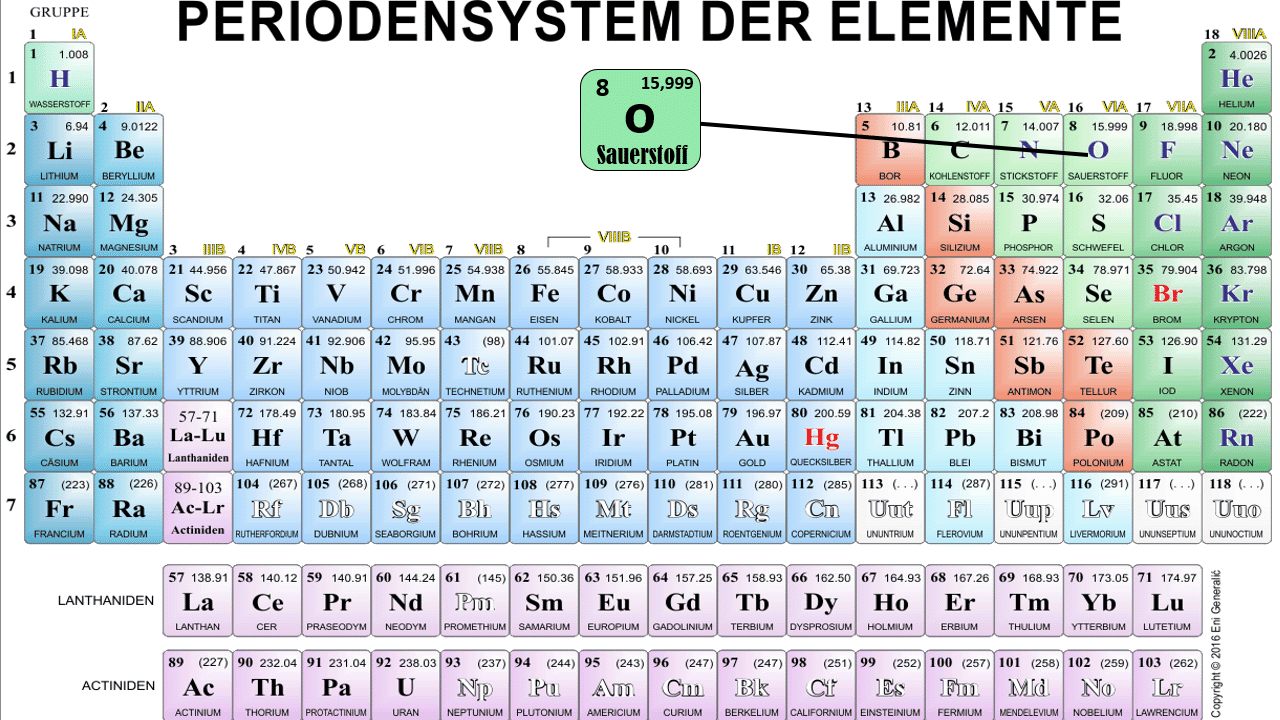
Periodensystem, PH5 — E. Generalic, https://www.periodni.com/gallery/images.html

Aus dem Periodensystem lesen wir ab:

$O = 15,999 u$

Für das Sauerstoffmolekül O₂ gilt dann:

$2 \cdot O = 2 \cdot 15,999u = 31,998 u$

Dies entspricht der molare Masse in g/mol:

$M_{O2} = 31,9998 u = 31,998 \frac{g}{mol}$

Umrechnen in kg/mol:

$M_{O2} = 31,998 \frac{0,001 kg}{mol} = 31,998 \cdot 0,001 \frac{kg}{mol} = 0,031998 \frac{kg}{mol}$

Die spezifische Gaskonstante kann wie folgt berechnet werden:

$R_I = \frac{R}{M}$

Die allgemeine Gaskonstante ist:

$R = 8,31446 \frac{J}{mol \cdot K}$

Einsetzen ergibt:

$R_i = \frac{8,31446 \frac{J}{mol \cdot K}}{0,031998 \frac{kg}{mol}} = 259,84 \frac{J}{kg \cdot K}$

Nachdem wir die spezifische Gaskonstante für Sauerstoff berechnet haben, können wir als nächstes die nach der gesuchten Größe m aufgelöste Zustandsgleichung des idealen Gases heranziehen:

$m = \frac{18.000.000 Pa \cdot 0,15m^3}{259,84 \frac{J}{kg \cdot K} \cdot 295,15 K} = 35,21 kg$