(WT3-18) – Smith-Diagramm | Erklärung, Zeichnung, Beispiele

Nachdem du bereits die Wöhlerkurven kennengelernt hast, betrachten wir nun im zweiten Schritt das sich daraus ergebende Smith-Diagramm (Engl. Smith-Chart).

Das Smith-Diagramm wird genutzt um die Dauerfestigkeit eines Werkstoffes zu bestimmen. Wir betrachten es für den Zugbereich und Druckbereich.

Für ein optimales Verständnis helfen dir zwei ausführliche Erklärungen/Anleitungen zur Vorgehensweise zur Erstellung des Diagramms für den Zugbereich und den Druckbereich.

Mehr zu diesem Thema und der Werkstofftechnik findest du im Kurs: WT3-Werkstoffprüfung

Smith-Diagramm – Grundlagen

“Das Smith-Diagramm ergibt sich aus mehreren Wöhlerkurven und gibt somit den gesamten Bereich einer Dauerschwingbeanspruchung wieder.“

Wie bereits eingangs erwähnt ergibt sich das Smith-Diagramm als Dauerfestigkeitsdiagramm aus mehreren Wöhlerkurven mit unterschiedlichen $\sigma_D$ .

Schwingbereiche beim Dauerschwingversuch

Formal ergibt sich für die Dauerschwingfestigkeit

$\sigma_D = \sigma_m \pm \sigma_A$

Kennzahlen

$\sigma_D =$ Dauerschwingfestigkeit

$\sigma_m =$ Mittelspannung

$\sigma_A =$ Spannungsausschlag

Anforderung & Zweck

Aus dem Smith-Diagramm lässt sich die Dauerschwingfestigkeit in Abhängigkeit von jeder angegebenen Mittelspannung ablesen.

Ein Konstrukteur kann mit den Smith-Diagrammen die Bemessung von Bauteilen vornehmen, die schwingend beansprucht werden.

Erstellen des Diagramms

In der nächsten Abbildung siehst du typisches Dauerfestigkeitsdiagramm nach Smith.

Smith-Diagramm, Dauerfestigkeitsdiagramm

Auf der Abszisse ist die Mittelspannung $\sigma_m$ und auf der Ordinate jeweils die Oberspannung $\sigma_o$ und die Unterspannung $\sigma_u$ aufgetragen.

Die Hilfslinie wird mit Winkel von 45 ° eingezeichnet. Dadurch erscheinen die Mittelspannungswerte auch als Ordinatenwerte.

Es ist dadurch möglich direkt

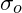$\sigma_o$ Oberspannung,
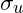$\sigma_u$ Unterspannung,
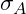$\sigma_A$ Spannungsausschlag sowie
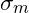$\sigma_m$ Mittelspannung

aus dem Smith-Diagramm abzulesen.

Die Werte $\sigma_o, \sigma_u$ und $\sigma_m$ , die zusammengehören, liegen vertikal übereinander.

Die Wechselfestigkeitswerte hingegen können auf der Abszissenachse abgelesen werden. Hier liegt die Schwellfestigkeit am Schnittpunkt der $\sigma_u$ – Kurve mit der Abzisse.

“In der Theorie verläuft das Smith-Diagramm bis zur Zugfestigkeit $R_m$

. Jedoch sei an dieser Stelle erwähnt, dass ab diesem Bereich die Betrachtung entfällt, da hier bereits plastische Verformungen auftreten, die vermieden werden sollen.”

Aus diesem Grund wird das Diagramm mit einer waagerechten Linie begrenzt. Diese Linie entspricht der statischen Streckgrenze $R_e$ .

Das gesamte Diagramm lässt sich in drei Bereiche unterteilen.

Schwellbereich – Druck
Wechselbereich
Schwellbereich – Zug

Vereinfachung

Aus Gründen der Vereinfachung ersetzt man die Kurvenverläufe für die Oberspannung und Unterspannung durch Geraden (Goodman-Geraden [rot]). Dadurch erhält man ein vereinfachtes Smith-Diagramm für den Zugbereich wie in der nächsten Abbildung dargestellt. Beim Smith-Diagramm für den Druckbereich verfährt man ebenso.

Für die Anfertigung eines Smith-Diagramm für den Zugbereich geht man nach einem festgelegten Schema vor. Hierzu benötigt man im Vorfeld die Angabe der Zugfestigkeit $R_m$ als obere Begrenzung. Sowie die Angabe der Streckgrenzen $R_{p0,2}$ und die Wechselsfestigkeit $\sigma_w$ des entsprechenden Werkstoffes.

So wird es gemacht!

Nachfolgend ist das Schema aufgeführt:

Nachdem wir bereits die 45°-Linie als Hilfslinie eintragen haben und diese durch die Linie der Zugfestigkeit 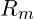$R_m$ begrenzt wurde, tragen wir mit 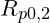$R_{p0,2}$ die Streckgrenze ein. Danach wird am Schnittpunkt von Hilfslinie und Zugfestigkeit der halbe Betrag aus der Wechselfestigkeit 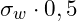$\sigma_w \cdot 0,5$ nach links abgetragen.
Ausgehend von diesem Punkt ziehen wir eine Gerade zu 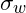$\sigma_w$ . Diese Linie ist die Begrenzung für die Oberspannung. Eine weitere Gerade ist dann die horizontale Linie von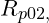 $R_{p02,}$
Die Gerade welche die Unterspannung 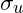$\sigma_u$ begrenzt, ergibt sich aus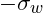 $- \sigma_w$
Jetzt trägt man unterhalb der Hilfslinie den Betrag der Ausschlagsspannung zwischen der Hilfslinie und dem Schnittpunkt von der 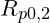$R_{p0,2}$ -Geraden mit der begrenzenden Linie der Oberspannung ab. Dadurch erhält man den 2. Punkt.
Im letzten Schritt schließt man den Geradenzug dadurch, dass man eine Verbindung zum Schnittpunkt der Hilfsgeraden mit der 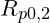$R_{p0,2}$ -Geraden zieht.

Darstellung des Zugbereichs – Vorgehensweise

Jetzt nehmen wir nochmal basierend auf den obigen Schritten eine besonders detaillierte Anfertigung vor.

Wie es sich für einen Techniker gehört, werden bevor man überhaupt Werte einträgt, die Achsen richtig beschriftet:

Y-Achse: Unterspannung und Oberspannung
X-Achse: Mittelspannung.
Hilfslinie: Winkelhalbierende ist die Mittelspannung und geht um Ursprung aus.

Ist eine Mittelspannung mit dem Wert $\sigma_m = 0$ gegeben, so hat man den Wert für die Wechselfestigkeit $\sigma_w$ des Werkstoffs.

Die Oberspannung ist dann $\sigma_o = + \sigma_w$ und die Unterspannung ist $\sigma_u = - \sigma_w$ .

Die beiden Werte für die Ober- und Unterspannung trägt man auf dem positiven und negativen Abschnitt der X-Achse auf.

Die Zugfestigkeit $R_m$ tragen wir sowohl auf der X-Achse, als auch Y-Achse, ab.

In dem Punkt wo sich die Gerade der Zugfestigkeit $R_m$ und der Mittelspannung $\sigma_m$ treffen, dort ist ein erster Fixpunkt.

“Über diesen Punkt hinweg werden keine Spannungswerte mehr ermittelt, da hier eine plastische Verformung eintritt.”

Dennoch gilt es zu beachten, dass sowohl die Kurve für die Oberspannung, als auch die Kurve für die Unterspannung dem Wert der Zugfestigkeit entsprechen und folglich auf diesen Punkt zulaufen.

Goodman-Gerade

Wie bereits oben erwähnt, dienen die Goodman-Geraden der Vereinfachung und Glättung der Oberspannungs- sowie Unterspannungskurven.

Begrenzung der Oberspannung

Ab jetzt benötigen wir eine zusätzliche Begrenzung. Diese Begrenzung ist der Streckgrenze $R_e$ , welche sicherstellt, dass keine unzulässigen Verformungen, wie sie oberhalb der Streckgrenze möglich sind, auftreten.

Diese horizontale Linie (Oberspannungslinie [gelb]) schneidet die Gerade der Oberspannung (I) und der Mittelspannung (II), wobei letztere nicht oberhalb der Streckgrenze verlaufen darf.

Begrenzung der Unterspannung

Wie du bereits weißt, besteht eine Symmetrie zwischen der Oberspannung und Unterspannung in Hinblick auf die Mittelspannung. Daher müssen auch die Unterspannungswerte begrenzt werden.

Hierzu tragen wir den vertikalen Abstand $m$ zwischen dem Punkt (I) und der Mittelspannung nochmals nach unten ab und erhalten somit im Punkt (III) die Begrenzung für die Unterspannung.

Schnittpunkt für die Unterspannung im Smith-Diagramm — Schnittpunkt für die Unterspannung

Dauerfestigkeitsbereich

Wenn wir jetzt den Bereich von der Goodman-Geraden der Oberspannung, Punkt I, II, III und der Goodman-Geraden der Unterspannung umranden, so ergibt sich daraus eine Fläche welche den wichtigen Dauerfestigkeitsbereich darstellt:

Bereich der Dauerfestigkeit im Smith-Diagramm — Bereich der Dauerfestigkeit

Fazit:

Mit dem letzten Schritt haben wir den Dauerfestigkeitsbereich festgelegt und können in diesem Bereich für jede Mittelspannung sowohl die zulässige Oberspannung als auch zulässige Unterspannung für den Werkstoff ablesen. Bis zu diesen Grenzwerten ist ein dauerhafter Einsatz möglich.

Darstellung des Druckbereichs – Vorgehensweise

Wer A sagt muss auch B sagen, so ungefähr verhält es sich auch zwischen dynamischen Zug- und Druckbeanspruchungen. Hier sieht das Smith-Diagramm für den dynamischen Druckbeanspruchungsfall anders aus. Ausgehend von unserem bisherigen Smith-Diagramm tragen wir nun die negativen Mittelspannungswerte ab. Diese sind negativ, da es sich jetzt um eine Druckbeanspruchung handelt.

Begrenzung der Oberspannung

Bisher haben wir immer die Streckgrenze als Begrenzung der Oberspannung genutzt, dies macht jetzt wenig Sinn, weshalb wir anstelle dessen die Quetschgrenze $\sigma_dF$ heranziehen.

Im Punkt (IV) ist diese Begrenzung verdeutlicht. Diese horizontale Linie betrifft ebenfalls die Gerade der negativen Mittelspannung (V).

Begrenzung der Unterspannung

Anders als bisher tragen wir nun den Abstand zwischen Oberspannung und Mittelspannung nach oben ab. Dieser Punkt (VI) begrenzt die Unterspannung im Druckbereich.

Dauerfestigkeitsbereich

Verbinden wir jetzt die Goodman-Gerade der Oberspannung, die Punkte VI, V, IV, sowie die Goodman-Gerade der Unterspannung mit einander, so erhalten wir als Flächeninhalt den Dauerfestigkeitsbereich für eine dynamische Druckbeanspruchung.

Fazit

Was kommt als Nächstes?

Nachdem du jetzt den Dauerschwingversuch als eine weitere Variante der Prüfverfahren kennengelernt hast und jetzt weißt wofür das Smith-Diagramm dient, stellen wir dir im kommenden Kursabschnitt den Zugversuch vor, welcher nach einem anderen Prinzip durchgeführt wird.

Was gibt es noch bei uns?

Optimaler Lernerfolg durch tausende Übungsaufgaben

Quizfrage 1

Quizfrage 2

“Wusstest du, dass unter jedem Kursabschnitt eine Vielzahl von verschiedenen interaktiven Übungsaufgaben bereitsteht, mit denen du deinen aktuellen Wissensstand überprüfen kannst?”

Alle Technikerschulen im Überblick

Zum Verzeichnis der Technikerschulen (Alles Rund um die Schulen) — Zum Verzeichnis der Technikerschulen

Kennst du eigentlich schon unser großes Technikerschulen-Verzeichnis für alle Bundesländer mit allen wichtigen Informationen (Studiengänge, Kosten, Anschrift, Routenplaner, Social-Media) ? Nein? – Dann schau einfach mal hinein:

Was ist Technikermathe?

Unser Dozent Jan erklärt es dir in nur 2 Minuten!

Oder direkt den > kostenlosen Probekurs < durchstöbern? – Hier findest du Auszüge aus jedem unserer Kurse!

Geballtes Wissen in derzeit 27 Kursen

Hat dir dieses Thema gefallen? – Ja? – Dann schaue dir auch gleich die anderen Themen zu den Kursen

WT3 (Werkstoffprüfung) und
TM1 (Technische Mechanik – Statik) an.

Lerne nun erfolgreich mit unserem Onlinekurs Technische Mechanik 1 — TM1 (Technische Mechanik)

Lerne nun erfolgreich mit unserem Onlinekurs Werkstofftechnik 3 — WT3 (Werkstoffprüfung)

Perfekte Prüfungsvorbereitung für nur 14,90 EUR/Jahr pro Kurs

++ Günstiger geht’s nicht!! ++

Oder direkt Mitglied werden und Zugriff auf alle 27 Kurse (inkl. Webinare + Unterlagen) sichern ab 7,40 EUR/Monat ++ Besser geht’s nicht!! ++