MA4 – Vektoraddition | Addition von Vektoren

In dieser Lerneinheit behandeln wir die Vektoraddition. Wir zeigen dir außerdem die grafische Vektoraddition sowie das Kommutativgesetz und das Assoziativgesetz der Vektoraddition auf.

Für ein optimales Verständnis helfen dir drei ausführliche Beispiele mit Zahlenwerten zu dem Thema.

Mehr zu diesem Thema und der Mathematik findest du im Kurs: MA4 – Vektorrechnung

Oder lieber mit den Grundlagen starten? Alles dazu findest du im Kurs: Ma1-Grundlagen der Mathematik

Vektoraddition – Grundlagen

Vektoren können miteinander addiert werden. Um zwei Vektoren miteinander zu addieren, werden die jeweiligen x-Werte und y-Werte der Vektoren miteinander addiert.

Vektoraddition?

Die Vektoraddition ist ein grundlegendes Konzept in der Mathematik und Physik, das häufig in der analytischen Geometrie und Vektorrechnung verwendet wird. Es beschreibt, wie zwei oder mehr Vektoren addiert werden, um einen neuen Vektor zu erhalten.

Grundprinzipien

Definition der Vektoraddition:
- Die Vektoraddition ist der Prozess, bei dem zwei Vektoren durch Addition ihrer jeweiligen Komponenten kombiniert werden.
Mathematische Darstellung:
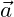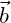- Für zwei Vektoren $\vec{a}$ und $\vec{b}$ mit den Komponenten $\vec{a} = (a_1, a_2, a_3)$ und $\vec{b} = (b_1, b_2, b_3)$ lautet die Vektoraddition: $\vec{c} = \vec{a} + \vec{b} = (a_1 + b_1, a_2 + b_2, a_3 + b_3)$
Eigenschaften der Vektoraddition:
- Kommutativität: $\vec{a} + \vec{b} = \vec{b} + \vec{a}$
- Assoziativität: $(\vec{a} + \vec{b} ) + \vec{c} = \vec{a} + (\vec{b} + \vec{c}$
- Existenz eines Nullvektors: $\vec{a} + \vec{0} = \vec{a}$
- Existenz eines inversen Vektors: $\vec{a} + (-\vec{a}) = \vec{0}$

Vektoraddition

Wir betrachten die folgenden zwei Vektoren:

$\vec{a} = \left( \begin{array}{c} x_1 \\ y_1 \end{array} \right)$

$\vec{b} = \left( \begin{array}{c} x_2 \\ y_2 \end{array} \right)$

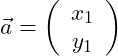
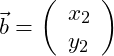
Die Addition der beiden Vektoren wird wie folgt durchgeführt:

Vektoraddition

$\vec{a} + \vec{b} := \left( \begin{array}{c} x_1 + x_2 \\ y_1 + y_2 \end{array} \right)$

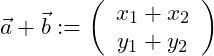
Betrachten wir hierzu ein Beispiel:

Gegeben seien die folgenden beiden Vektoren:

$\vec{a} = \left( \begin{array}{c} 1 \\ 2 \end{array} \right)$

$\vec{b} = \left( \begin{array}{c} -2 \\ 3 \end{array} \right)$

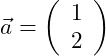
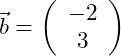
Führe die Vektoraddition durch!

Wir wollen die beiden oben angegebenen Vektoren miteinander addieren. Dazu addieren wir die zugehörigen x-Werte und y-Werte der beiden Vektoren miteinander:

$\vec{a} + \vec{b} = \left( \begin{array}{c} 1 + (-2) \\ 2 + 3 \end{array} \right)$

$\vec{a} + \vec{b} = \left( \begin{array}{c} 1 -2 \\ 2 + 3 \end{array} \right)$

$\vec{a} + \vec{b} = \left( \begin{array}{c} -1 \\ 5 \end{array} \right)$

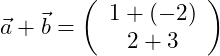
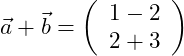
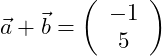
Die grafische Vektoraddition ergibt sich wie folgt:

Wir haben die beiden Vektoren $\vec{a}$ und $\vec{b}$ gegeben. Wir können nun eine grafische Vektoraddition durchführen, indem wir den Anfangspunkt des Vektors $\vec{b}$ an die Spitze des Vektors $\vec{a}$ legen. Der Summenvektor $\vec{a}$ + $\vec{b}$ ergibt sich dann, indem wir den Anfangspunkt an den Anfangspunk des 1.Vektors (hier: $\vec{a}$ ) an die Spitze des letzten Vektors (hier: $\vec{b}$ ) legen.

Kommutativgesetz und Vektoraddition

$\vec{a}$ + $\vec{b}$ = $\vec{b}$ + $\vec{a}$

Das Kommutativgesetz gilt bei der Addition von Vektoren und besagt, dass die Reihenfolge der Addition zum selben Ergebnis führt.

Beispiel

Gegeben seien die beiden Vektoren

$\vec{a} = \left( \begin{array}{c} 2 \\ 1 \end{array} \right)$

$\vec{b} = \left( \begin{array}{c} 2 \\ 3 \end{array} \right)$

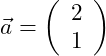
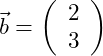
Wir erhalten den folgenden Summenvektor:

$\vec{a} + \vec{b} = \left( \begin{array}{c} 2 + 2 \\ 1 + 3 \end{array} \right) = \left( \begin{array}{c} 4 \\ 4 \end{array} \right)$

$\vec{b}+ \vec{a} = \left( \begin{array}{c} 2 + 2 \\ 3 + 1 \end{array} \right) = \left( \begin{array}{c} 4 \\ 4 \end{array} \right)$

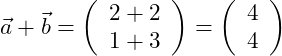
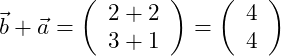
Betrachten wir die grafische Vektoraddition und das Kommutativgesetz:

Kommutativgesetz, Vektoren, Vektoraddition

Merk’s dir!

Die grafische Vektoraddition ist die Aneinanderreihung von Vektoren in einer beliebigen Reihenfolge. Du beginnst mit einem beliebigen Vektor und zeichnest diesen ein. Danach wählst du den nächsten Vektor (beliebig) und legst diesen mit seinem Anfangspunkt an die Spitze des vorangegangenen Vektors. Diese Schritte führst du solange aus, bis du alle Vektoren einmal berücksichtigt hast. Die Reihenfolge der Kräfte ist dabei beliebig wählbar.

Der Summenvektor ergibt sich dann, indem du den Anfangspunkt des Summenvektors an den Anfangspunkt des zuerst gewählten Vektors legst und die Spitze des Summenvektors an die Spitze des zuletzt gewählten Vektors.

Assoziativgesetz und Vektoraddition

Das Assoziativgesetz besagt, dass du Klammern bei einer Addition beliebig setzen kannst. Das Ergebnis ändert sich dabei nicht.

$(\vec{a} + \vec{b}) + \vec{c} = \vec{a} + (\vec{b} + \vec{c}) = \vec{a}+ \vec{b} + \vec{c}$

mit

$(\vec{a} + \vec{b}) = \vec{s_1}$

$(\vec{b} + \vec{c}) = \vec{s_2}$

Beispiel

Gegeben seien die folgenden drei Vektoren:

$\vec{a} = \left( \begin{array}{c} 2 \\ 1 \end{array} \right)$

$\vec{b} = \left( \begin{array}{c} 2 \\ 3 \end{array} \right)$

$\vec{c} = \left( \begin{array}{c} -2 \\ 1 \end{array} \right)$

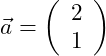
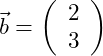
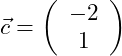
Zunächst berechnen wir:

$(\vec{a} + \vec{b}) + \vec{c}$

Wir addieren also zunächst die beiden Vektoren a und b miteinander:

$\vec{a} + \vec{b} = \left( \begin{array}{c} 2 + 2 \\ 1 + 3 \end{array} \right)$

$\vec{s_1} = \vec{a} + \vec{b} = \left( \begin{array}{c} 4 \\ 4 \end{array} \right)$

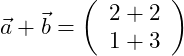
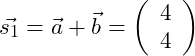
Als nächstes addieren wir dieses Ergebnis zu Vektor c:

$\vec{s_1} + \vec{c} = \left( \begin{array}{c} 4 + (-2) \\ 4 + 1 \end{array} \right)$

$\vec{s_1} + \vec{c} = \left( \begin{array}{c} 2 \\ 5 \end{array} \right)$

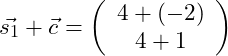
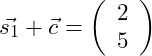
Nun betrachten wir:

$\vec{a} + (\vec{b} + \vec{c})$

Wir addieren Vektor b und c miteinander:

$\vec{s_2} = \vec{b} + \vec{c} = \left( \begin{array}{c} 0 \\ 4 \end{array} \right)$

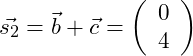
Jetzt addieren den Vektor a mit diesem Ergebnis:

$\vec{a} + \vec{s_2} = \left( \begin{array}{c} 2 \\ 5 \end{array} \right)$

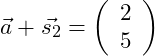
Und zum Schluss addieren wir alle drei Vektoren zusammen:

$\vec{a}+ \vec{b} + \vec{c} = \left( \begin{array}{c} 2 + 2 + (-2) \\ 1 + 3 + 1 \end{array} \right)$

$\vec{a}+ \vec{b} + \vec{c} = \left( \begin{array}{c} 2 \\ 5 \end{array} \right)$

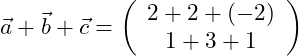
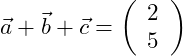
Für die Vektoraddition gilt das Assoziativgesetz. In der nachfolgenden Grafik siehst du das Beispiel grafisch veranschaulicht:

Assoziativgesetz, Vektoraddition, Vektoren

Wir haben die drei Vektoren a, b und c gegeben. Das Ergebnis ist in allen drei Berechnungsfällen identisch und ergibt am Ende den Vektor (2,5).

Nullvektor

Von einem Nullvektor ist dann die Rede, wenn bei der Vektoraddition der Vektor zu Null wird:

$\vec{0} = \vec{a} + \vec{b} + \vec{c} + ... + \vec{n}$

Beispiel

Gegeben seien die drei Vektoren:

$\vec{a} = \left( \begin{array}{c} 2 \\ 1 \end{array} \right)$

$\vec{b} = \left( \begin{array}{c} 2 \\ -2 \end{array} \right)$

$\vec{c} = \left( \begin{array}{c} -4 \\ 1 \end{array} \right)$

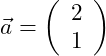
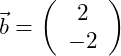
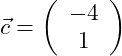
Wir bilden die Summe aus den drei Vektoren:

$\vec{a} + \vec{b} + \vec{c} = \left( \begin{array}{c} 2 + 2 + (-4) \\ 1 + (-2) + 1 \end{array} \right)$

$\vec{a} + \vec{b} + \vec{c} = \left( \begin{array}{c} 0 \\ 0 \end{array} \right)$

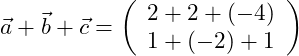
Für die grafische Vektoraddition ist dann der Nullvektor gegeben, wenn der Anfangspunkt des ersten Vektors mit dem Endpunkt des letzten Vektors zusammenfällt:

In der obigen linken Grafik sind die drei Vektoren eingezeichnet. Mittels Vektoraddition werden diese nacheinander (in beliebiger Reihenfolge) aneinandergereiht (rechte Grafik). Dabei berührt die Spitze des letzten Vektors (hier: $\vec{c}$ ) den Anfangspunkt des ersten Vektors (hier: $\vec{a}$ ). Damit ist es nicht möglich den Summenvektor $\vec{a} + \vec{b} + \vec{c}$ zu bilden. Dieser liegt normalerweise mit dem Anfangspunkt am Anfangspunkt des ersten Vektors und mit der Spitze an der Spitze des letzten Vektors.

Wir haben somit den Summenvektor mit Null gegeben (Nullvektor):

$\vec{a} + \vec{b} + \vec{c} = \left( \begin{array}{c} 0 \\ 0 \end{array} \right)$

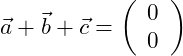
Anwendung der Vektoraddition

Physik: Addition von Kräften, Geschwindigkeiten und Beschleunigungen.
Ingenieurwesen: Berechnung von resultierenden Kräften und Bewegungen.
Computergraphik: Berechnung von Positionen und Transformationen in 3D-Räumen.

Mögliche Fragestellungen | Häufig gestellte Fragen (FAQs)

1. Was ist die Vektoraddition?

Die Vektoraddition ist das Verfahren, bei dem zwei oder mehr Vektoren durch Addition ihrer entsprechenden Komponenten kombiniert werden.

2. Welche Eigenschaften hat die Vektoraddition?

Sie ist kommutativ, assoziativ und es gibt einen Nullvektor, zudem liegt ein inverser Vektor vor.

3. Wie addiere ich zwei Vektoren?

Addiere die entsprechenden Komponenten der Vektoren.

4. Was ist der Nullvektor?

Der Nullvektor ist ein Vektor mit allen Komponenten gleich Null. Er verändert andere Vektoren nicht, wenn er addiert wird.

5. Kann ich mehr als zwei Vektoren gleichzeitig addieren?

Ja, die Vektoraddition ist assoziativ, sodass mehrere Vektoren schrittweise addiert werden können.

Zusammenfassung

Die Vektoraddition ist eine wesentliche Operation in der Vektorrechnung, die in vielen Bereichen der Mathematik, Physik und Technik Anwendung findet. Durch die Addition der entsprechenden Komponenten zweier Vektoren wird ein neuer Vektor erzeugt.

Dieses Konzept ist grundlegend für die Untersuchung von Vektoren und ihren Anwendungen in verschiedenen wissenschaftlichen und technischen Disziplinen.

Was kommt als Nächstes?

In der folgenden Lerneinheit zeigen wir dir, wie Ableiten mit der Produktregel abläuft.

Was gibt es noch bei uns?

Optimaler Lernerfolg durch tausende Übungsaufgaben

Übungsbereich (Demo) - Lerne mit mehr als 4000 Übungsaufgaben für deine Prüfungen — Übungsbereich (Demo) – Lerne mit mehr als 4000 Übungsaufgaben für deine Prüfungen

Quizfrage 1

Quizfrage 2

“Wusstest du, dass unter jedem Kursabschnitt eine Vielzahl von verschiedenen interaktiven Übungsaufgaben bereitsteht, mit denen du deinen aktuellen Wissensstand überprüfen kannst?”

Alle Technikerschulen im Überblick

Zum Verzeichnis der Technikerschulen (Alles Rund um die Schulen) — Zum Verzeichnis der Technikerschulen

Kennst du eigentlich schon unser großes Technikerschulen-Verzeichnis für alle Bundesländer mit allen wichtigen Informationen (Studiengänge, Kosten, Anschrift, Routenplaner, Social-Media) ? Nein? – Dann schau einfach mal hinein:

Was ist Technikermathe?

Unser Dozent Jan erklärt es dir in nur 2 Minuten!

Oder direkt den > kostenlosen Probekurs < durchstöbern? – Hier findest du Auszüge aus jedem unserer Kurse!

Geballtes Wissen in derzeit 26 Kursen

Hat dir dieses Thema gefallen? – Ja? – Dann schaue dir auch gleich die anderen Themen zu den Kursen

WT3 (Werkstoffprüfung) und
TM1 (Technische Mechanik – Statik) an.

Lerne nun erfolgreich mit unserem Onlinekurs Technische Mechanik 1 — TM1 (Technische Mechanik)

Lerne nun erfolgreich mit unserem Onlinekurs Werkstofftechnik 3 — WT3 (Werkstoffprüfung)

Perfekte Prüfungsvorbereitung für nur 14,90 EUR/Jahr pro Kurs

++ Günstiger geht’s nicht!! ++

Oder direkt Mitglied werden und Zugriff auf alle 26 Kurse (inkl. Webinare + Unterlagen) sichern ab 7,40 EUR/Monat ++ Besser geht’s nicht!! ++