Achsensymmetrie ist dann gegeben, wenn eine gegebene Fläche an einer Achse gespiegelt werden kann. Diese Achse wird dann auch als Symmetrieachsen bezeichnet. Wir wollen uns in diesem Zusammenhang anschauen was einfach symmetrische Querschnitte und doppelt symmetrische Querschnitte sind.
Achsensymmetrie – Doppelt symmetrische Querschnitte
Für die einachsige Biegung wollen wir Balken betrachten, die einen einfach oder doppelt symmetrischen Querschnitt bezüglich der y,z-Achsen aufweisen.
Bei einer Fläche ist Achsensymmetrie bezüglich einer Achse gegeben, wenn sie durch die Spiegelung an ihrer Achse auf sich selbst abgebildet wird:
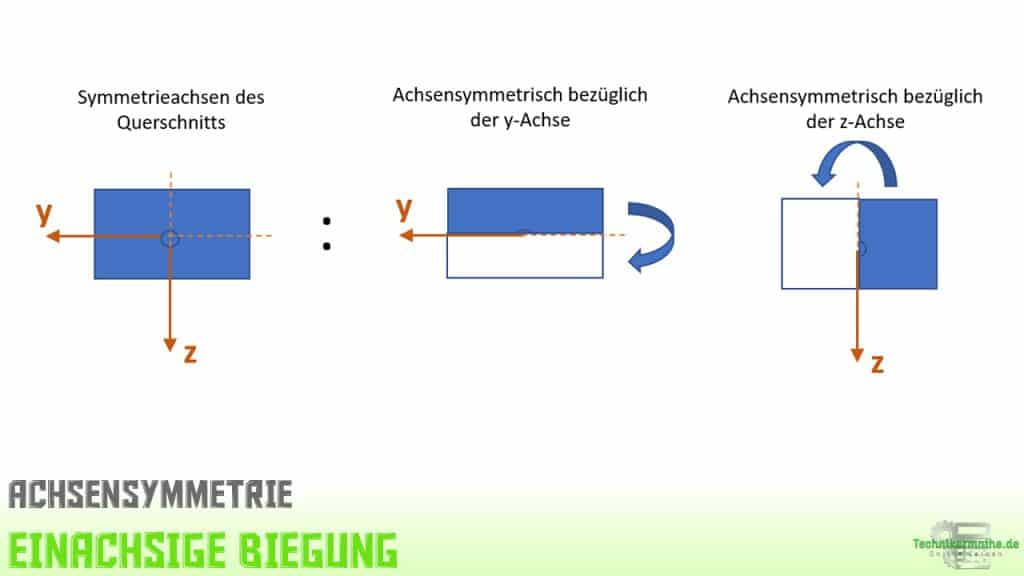
In der obigen Grafik ist ein Querschnitt eines Balkens zu sehen. Die y,z-Achsen liegen im Schwerpunkt der Querschnittsfläche. Die x-Achse (hier nicht abgebildet) zeigt aus der Grafik heraus und fällt mit der Balkenachse zusammen. Wir wollen nun zeigen, dass die beiden Achsen jeweils Symmetrieachsen des Querschnitts sind.
Schauen wir uns dazu zunächst die y-Achse an. Wenn wir die Fläche oberhalb der y-Achse an dieser spiegeln, so erhalten wir genau den unteren Teil. Damit ist die Querschnittsfläche achsensymmetrisch in Bezug auf die y-Achse und die y-Achse somit eine Symmetrieachse des Querschnitts.
Betrachten wir die z-Achse und spiegeln die rechte Fläche an dieser Achse, so erhalten wir genau die linke Fläche. Damit ist auch die z-Achse eine Symmetrieachse des Querschnitts.
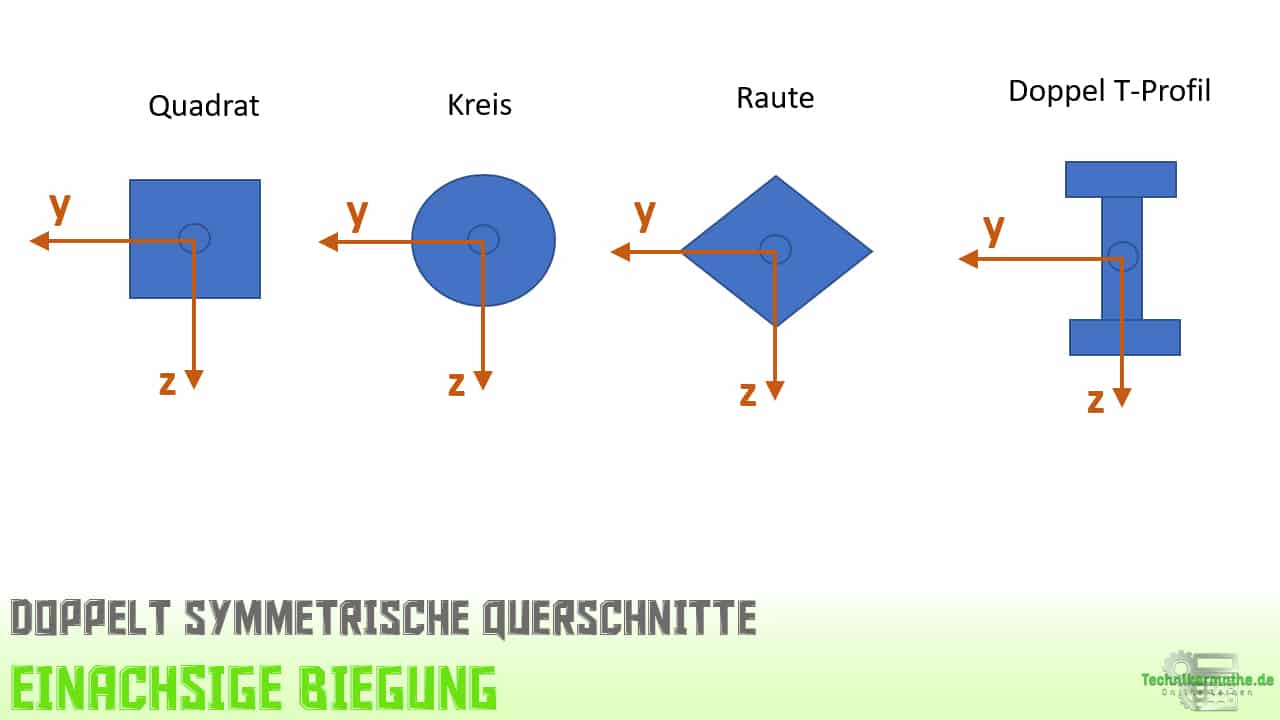
Sind beide y,z-Achsen Symmetrieachsen des Querschnitts, so liegt ein doppelt symmetrischer Querschnitt vor. Weitere Flächen, bei denen die y,z-Achsen Symmetrieachsen darstellen siehst du in der folgenden Grafik:
Achsensymmetrie – Einfach symmetrische Querschnitte
Wir wollen ebenfalls einfach symmetrische Querschnitte betrachten. In einem solchen Fall ist nur eine der beiden Achsen eine Symmetrieachse:
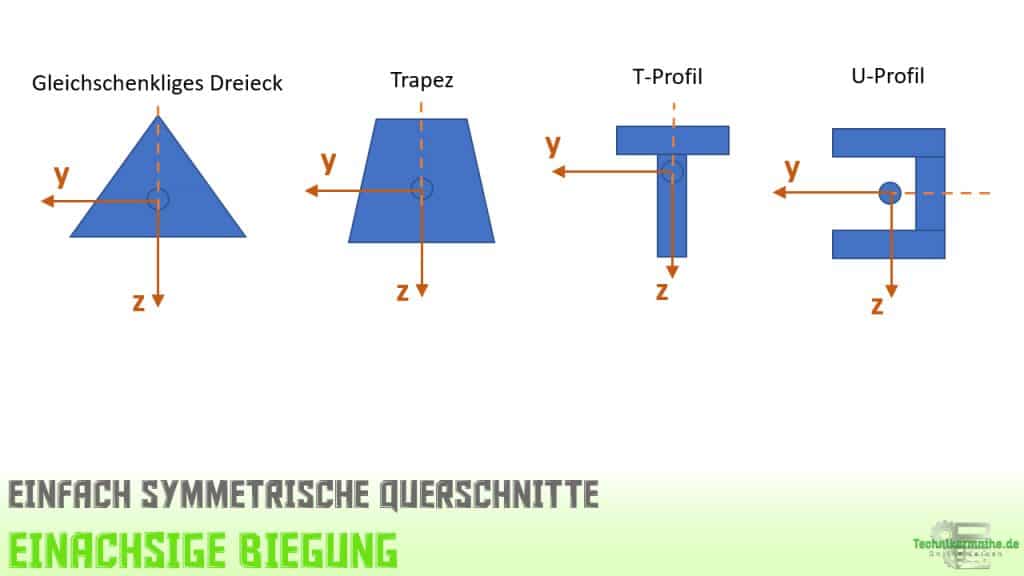
In der obigen Grafik siehst du einige ausgewählte Querschnitte die einfach symmetrisch in Bezug auf die y- oder z-Achse sind.
Die ersten drei Querschnitte sind achsensymmetrisch bezüglich der z-Achse. Die linke Fläche lässt sich also an der z-Achse spiegeln und es ergibt sich genau die Fläche rechts von der Achse. Für die y-Achse ist dies nicht gegeben, somit ist die y-Achse hier keine Symmetrieachse.
Für den 4. Querschnitt (U-Profil) ist die y-Achse die Symmetrieachse, weil sich die obere Fläche an der Achse so spiegelt, dass genau die untere Fläche resultiert. Die z-Achse hingegen ist hier keine Symmetrieachse.
Es liegen also in allen 4 Fällen einfach symmetrische Querschnitte vor.
Wir wollen im Folgenden immer davon ausgehen, dass einfach oder doppelt symmetrische Querschnitte gegeben sind.
In der nachfolgenden Lerneinheit behandeln wir die Flächenträgheitsmomente und zeigen dir, wie du diese berechnen kannst.
Was gibt es noch bei uns?
Optimaler Lernerfolg durch tausende Übungsaufgaben

Quizfrage 1
“Wusstest du, dass unter jedem Kursabschnitt eine Vielzahl von verschiedenen interaktiven Übungsaufgaben bereitsteht, mit denen du deinen aktuellen Wissensstand überprüfen kannst?”
Was ist Technikermathe?
Unser Dozent Jan erklärt es dir in nur 2 Minuten!
Oder direkt den > kostenlosen Probekurs < durchstöbern? – Hier findest du Auszüge aus Alle Onlinekurse Technikermathe!
Geballtes Wissen in derzeit 26 Kursen
Hat dir dieses Thema gefallen? – Ja? – Dann schaue dir auch gleich die anderen Themen zu den Kursen
WT3 (Werkstoffprüfung) und
TM1 (Technische Mechanik – Statik) an.


Perfekte Prüfungsvorbereitung für nur 14,90 EUR/Jahr pro Kurs
++ Günstiger geht’s nicht!! ++
Oder direkt Mitglied werden und Alle unsere Onlinekurse (inkl. Webinare + Unterlagen) sichern ab 7,40 EUR/Monat ++ Besser geht’s nicht!! ++
Social Media? - Sind wir dabei!
Dein Technikermathe.de-Team






