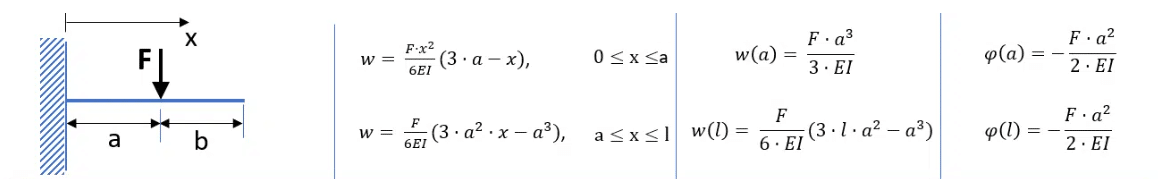TM2 – Superposition: Biegelinie mit zwei Einzelkräften [Beispiel, Formeln, Lösung]

Das Superpositionsprinzip besagt, dass wir das Problem in einfachere Teilprobleme zerlegen, für welche wir die Lösung bereits kennen. Durch Überlagerung (= Superposition) dieser bekannten Lösungen, erhalten wir die Gesamtlösung ohne komplizierte Berechnungen durchzuführen.

In diesem Fall betrachten wir einen Balken mit zwei Einzelkräften und zerlegen diesen Balken in zwei Balken mit jeweils einer Einzelkraft. Die Biegelinien für die beiden Teilprobleme lesen wir aus Tabellenwerken ab und überlagen diese Biegelinien, so dass wir am Ende zu der Lösung gelangen, ohne komplizierte Berechnungen durchführen zu müssen.

In dieser Prüfungsaufgabe betrachten wir einen Kragarm, der durch zwei vertikale Einzelkräfte belastet wird. Wir wollen die Biegelinie bestimmen, indem wir das Superpositionsprinzip anwenden.

Mehr zu diesem Thema und der Mechanik findest du im Kurs: TM2 – Festigkeitslehre.

Oder lieber mit den Grundlagen starten? Alles dazu findest du im Kurs: Ma1-Grundlagen der Mathematik

Aufgabe: Kragarm mit zwei Einzelkräften

Aufgabenstellung

Gegeben sei der obige Balken mit den zwei vertikalen Einzelkräften F₁ und F₂. Der Balken ist auf der linken Seite fest eingespannt und hat auf der rechten Seite ein freies Ende. Die Biegesteifigkeit EI sei konstant.

a) Bestimme die Biegelinien für beide Bereiche!

b) Bestimme die Durchbiegung beim Kraftangriff F₁ und F₂.

Lösung a) Biegelinien

Wir betrachten den Kragarm mit den folgenden Annahmen:

Die Länge des Balkens beträgt L.
Eine vertikale Kraft F₁ wirkt an der Stelle x = a und eine vertikale Kraft F₂ wirkt an der Stelle x = L.
Der Balken ist am linken Ende (bei x=0) eingespannt, das rechte Ende (bei x = L) ist frei.
Die Biegesteifigkeit des Balkens ist konstant und wird mit EI bezeichnet, wobei E der Elastizitätsmodul und I das Flächenmoment 2. Ordnung des Balkens ist.

Die übliche Vorgehensweise wäre jetzt:

Auflagerkräfte berechnen.
Schnittbereiche bestimmen und Schnittmoment berechnen. Dazu müssen wir den Balken in zwei Schnittbereiche zerlegen. Einen Schnittbereich vor der Kraft F₁ und einen nach der Kraft F₁.
Biegelinien für die beiden Bereiche aus Integration von 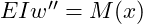$EIw'' = M(x)$ bestimmen.

Wir wenden hier aber das Superpositionsprinzip an, indem wir Tabellenwerke für jeden Schnittbereich hinzuziehen.

Bereich 1 und 2: Kraft F₁

In der obigen Grafik ist ein Kragarm mit einer vertikalen Einzelkraft am freien Ende gegeben. Wir betrachten nun zunächst nur die Kraft F₁und die Auswirkungen auf die Biegelinie (siehe auch vorangegangene Lerneinheit).

Die Kraft F₁ übt einen direkt einen Einfluss auf den 1. Bereich (0 ≤ x ≤ a) aus. Hier ergibt sich eine kubische Funktion bis zum Kraftangriff von F₁. Im zweiten Bereich ist keine Kraft mehr gegeben, aber die Biegelinie verläuft weiter linear mit dem Neigungswinkel -φ der sich bei x = a ergibt.

Wir beginnen zunächst die Biegelinie für den 1. Bereich aus der folgenden Tabelle (siehe Übersicht Biegelinien) zu entnehmen:

Wir können also die Biegelinie für den 1. Bereich übernehmen:

Biegelinie 1. Bereich der Kraft F₁

$w^{F1}_1(x) = \dfrac{F_1 \cdot x^2}{6 \cdot EI} (3a - x)$

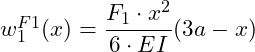
Wir müssen hier aber anstelle der Länge l die Länge a berücksichtigen, da der 1.Bereich eine Länge von a aufweist. Die Biegelinie im 1. Bereich ist infolge des Kraftangriffs F₁ eine kubische Funktion.

Wir betrachten als nächstes den Bereich 2.

Wir haben im 1. Bereich eine kubische Funktion gegeben, da hier ein Schnittmoment M infolge der Kraft F₁ auftritt. Da im 2. Bereich nach x = a keine Kraft und kein Moment mehr an den Balken angreift, muss die Biegelinie linear verlaufen, weil das Moment M = 0 ist.

Merk’s dir!

$EIw'' = M(x) = 0$

$EIw' = \int 0 \; dx = 0 + C_1 = C_1$

$EIw = \int C_1 \; dx = C_1 \cdot x + C_2$

Damit ergibt sich eine lineare Biegelinie im 2.Bereich.

Wir suchen also die lineare Biegelinie im Bereich a ≤ x ≤ L infolge der Kraft F₁. Wir können eine lineare Funktion über die allgemeine Funktionsgleichung bestimmen:

$w^{F1}_2 = mx + b$

Die Steigung m ist nichts anderes als die Ableitung der Biegelinie. Diese Steigung m entspricht der Steigung der Biegelinie am Ende des 1. Bereichs, denn es gilt:

$w^{F1}'_1(x = a) = w^{F1}'_2(x = a)$

Merk’s dir!

Das bedeutet, dass die Ableitung der Biegelinie im 1. Bereich gleich der Ableitung der Biegelinie im 2. Bereich ist, wenn wir x = a betrachten.

Wir können hier also die Biegelinie des 1. Bereichs heranziehen, ableiten und dann x = a einsetzen. Wir haben dann den Neigungswinkel gegeben, mit dem sich der Balken im Bereich 2 weiter neigt.

Diesen Neigungswinkel erhalten wir, wenn wir die 1. Ableitung der Biegelinie aus dem 1. Bereich bilden:

$w^{F1}_1(x) = \dfrac{F_1 \cdot x^2}{6 \cdot EI} (3a - x) = \dfrac{3F_1 \cdot a \cdot x^2 - F_1 \cdot x^3}{6EI}$

$w^{F1}_1'(x) = - \varphi = \dfrac{6F_1 \cdot a \cdot x - 3F_1 \cdot x^2}{6 \cdot EI}$

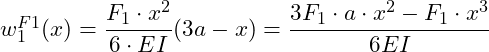
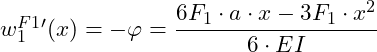
Einsetzen von x = a, weil wir den Neigungswinkel am Ende des 1. Bereichs suchen:

$w^{F1}_1'(x = a) = - \varphi = \dfrac{6F_1 \cdot a^2 - 3F_1 \cdot a^2}{6 \cdot EI} = \dfrac{F_1 \cdot a^2}{2 EI}$

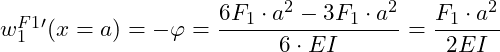
Der Neigungswinkel entspricht der 1. Ableitung und damit der Steigung der Funktion:

$- \varphi = m = \dfrac{F_1 \cdot a^2}{2 EI}$

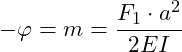
Wir können den Neigungswinkel auch aus der obigen Tabelle ablesen:

Wir haben hier den Neigungswinkel $\varphi(l)$ gegeben. Wir müssen hier l = a setzen und erhalten:

$-\varphi(a) = m = \dfrac{F_1 \cdot a^2}{2 EI}$

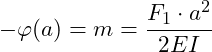
Wir können die Steigung m nun in die allgemeine Funktionsgleichung einsetzen:

$w^{F1}_2 = mx + b$

$w^{F1}_2(x) = \dfrac{F_1 \cdot a^2}{2 EI} \cdot x + b$

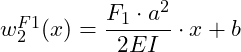
Wir betrachten hier den 2. Bereich, der bei x = a startet. Wir müssen dementsprechend x ersetzen durch $x - a$ :

$w^{F1}_2(x) = \dfrac{F_1 \cdot a^2}{2 EI} \cdot (x - a) + b$

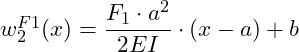
Wir suchen zum Schluss noch den Schnittpunkt mit der z-Achse für den 2. Bereich. Die Biegelinie des 2. Bereichs $w_2(x)$ beginnt dort, wo die Biegelinie des 1. Bereichs $w_1(x)$ endet. Damit ziehen wir wieder die Gleichung des 1. Bereichs heran und setzen x = a ein:

$b = \dfrac{F_1 \cdot a^2}{6 \cdot EI} (3a - a) = \dfrac{2F_1 \cdot a^3}{6 \cdot EI} = \dfrac{F_1 \cdot a^3}{3 \cdot EI}$

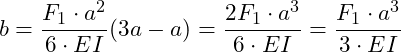
Wir können nun die Biegelinie für den 2. Bereich aufstellen:

$w^{F1}_2(x) = \dfrac{F_1 \cdot a^2}{2 EI} \cdot (x - a) + \dfrac{F_1 \cdot a^3}{3 \cdot EI}$

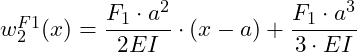
Zusammenfassen ergibt:

Biegelinie 2. Bereich der Kraft F₁

$w^{F1}_2(x) = \dfrac{F_1}{6 EI} (3 \cdot x \cdot a^2 - a^3)$

Dies entspricht genau der Biegelinien aus der folgenden Tabelle:

Wir haben die Biegelinien für den obigen Lastfall also bereits in der Tabelle im Abschnitt: (TM2-13a-9) Übersicht der Biegelinien gegeben. Ziel war es aber zu zeigen, wie die Biegelinie des 2. Bereichs aus der Biegelinie des 1. Bereichs ermittelt wird.

Bereich 1 und 2: Kraft F₂

Für die Kraft F₂ können wir ebenfalls die folgende Tabelle heranziehen:

Hier können wir die Gleichung für beide Bereiche übernehmen:

Biegelinie 1. und 2. Bereich der Kraft F₂

$w^{F2}_1(x) = \dfrac{F_2 \cdot x^2}{6 \cdot EI} (3L - x)$

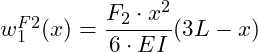
Diese Gleichung gilt hier für beide Bereiche, wobei für Bereich 1 nur Werte von 0 ≤ x ≤ a eingesetzt werden dürfen und für Bereich 2 nur Werte von a ≤ x ≤ L.

Biegelinie für beide Bereiche

Wir können nun für die beiden Bereiche die Biegelinien aufstellen.

Bereich 1 (0 ≤ x ≤ a):

$w_1 = w^{F1}_1(x) + w^{F2}_1(x)$

$w_1 = \dfrac{F_1 \cdot x^2}{6 \cdot EI} (3a - x) + \dfrac{F_2 \cdot x^2}{6 \cdot EI} (3L - x)$

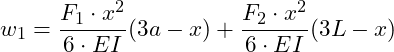
Bereich 2 (a ≤ x ≤ L):

$w_2 = w^{F1}_2(x) + w^{F2}_2(x)$

$w_2 = \dfrac{F_1}{6 EI} (3 \cdot x \cdot a^2 - a^3) + \dfrac{F_2 \cdot x^2}{6 \cdot EI} (3L - x)$

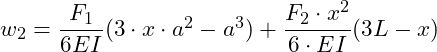
Lösung b) Durchbiegung

Wir wollen zunächst die Absenkung bei x = a bestimmen, dort wo die Kraft F₁ angreift. Hier können wir nun entweder den Bereich 1 oder 2 heranziehen, da bei x = a der Übergang der beiden Bereiche gegeben ist. Dazu setzen wir x = a in w₁ ein:

$w_1 = \dfrac{F_1 \cdot a^2}{6 \cdot EI} (3a - a) + \dfrac{F_2 \cdot a^2}{6 \cdot EI} (3L - a)$

$w_1 = \dfrac{F_1 \cdot a^3}{3 \cdot EI} + \dfrac{F_2 \cdot a^2}{6 \cdot EI} (3L - a)$

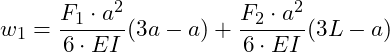
Als nächstes betrachten wir die Absenkung bei x = L, dort wo die Kraft F₂ angreift:

$w_2 = \dfrac{F_1}{6 EI} (3 \cdot L \cdot a^2 - a^3) + \dfrac{F_2 \cdot L^2}{6 \cdot EI} (3L - L)$

$w_2 = \dfrac{F_1}{6 EI} (3 \cdot L \cdot a^2 - a^3) + \dfrac{F_2 \cdot L^3}{3 \cdot EI}$

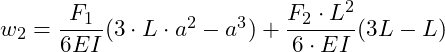
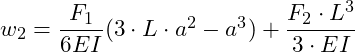
Einsetzen von Werten

Betrachten wir die folgenden Werte:

$a = 500mm$ , $L = 1.200mm$ , $EI = 2 \cdot 10^{11} Nmm^2$ , $F_1 = 3.500 N$ , $F_2 = 2.000N$

$w_1 = \dfrac{3.500 N \cdot (500mm)^3}{3 \cdot 2 \cdot 10^{11} Nmm^2} + \dfrac{2.000N \cdot (500mm)^2}{6 \cdot 2 \cdot 10^{11} Nmm^2} (3\cdot 1.200mm - 500mm)$

$w_1 = 2,021 mm$

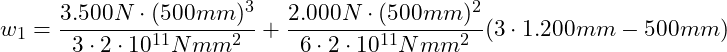
Die Absenkung bei x = a, dort wo die Kraft F₁ angreift beträgt 2,021 mm.

$w_2 = \dfrac{3.500 N}{6 \cdot 2 \cdot 10^{11} Nmm^2} (3 \cdot 1.200mm \cdot (500mm)^2 - (500mm)^3) + \dfrac{2.000N \cdot (1.200mm)^3}{3 \cdot 2 \cdot 10^{11} Nmm^2}$

$w_2 = 8,02mm$

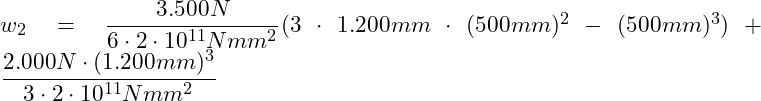
Was gibt es noch bei uns?

Optimaler Lernerfolg durch tausende Übungsaufgaben

Übungsbereich (Demo) - Lerne mit mehr als 4000 Übungsaufgaben für deine Prüfungen — Übungsbereich (Demo) – Lerne mit mehr als 4000 Übungsaufgaben für deine Prüfungen

Quizfrage 1

“Wusstest du, dass unter jedem Kursabschnitt eine Vielzahl von verschiedenen interaktiven Übungsaufgaben bereitsteht, mit denen du deinen aktuellen Wissensstand überprüfen kannst?”

Alle Technikerschulen im Überblick

Zum Verzeichnis der Technikerschulen (Alles Rund um die Schulen) — Zum Verzeichnis der Technikerschulen

Kennst du eigentlich schon unser großes Technikerschulen-Verzeichnis für alle Bundesländer mit allen wichtigen Informationen (Studiengänge, Kosten, Anschrift, Routenplaner, Social-Media) ? Nein? – Dann schau einfach mal hinein:

Was ist Technikermathe?

Unser Dozent Jan erklärt es dir in nur 2 Minuten!

Oder direkt den > kostenlosen Probekurs < durchstöbern? – Hier findest du Auszüge aus jedem unserer Kurse!

Geballtes Wissen in derzeit 26 Kursen

Hat dir dieses Thema gefallen? – Ja? – Dann schaue dir auch gleich die anderen Themen zu den Kursen

WT3 (Werkstoffprüfung) und
TM1 (Technische Mechanik – Statik) an.

Lerne nun erfolgreich mit unserem Onlinekurs Technische Mechanik 1 — TM1 (Technische Mechanik)

Lerne nun erfolgreich mit unserem Onlinekurs Werkstofftechnik 3 — WT3 (Werkstoffprüfung)

Perfekte Prüfungsvorbereitung für nur 14,90 EUR/Jahr pro Kurs

++ Günstiger geht’s nicht!! ++

Oder direkt Mitglied werden und Zugriff auf alle 26 Kurse (inkl. Webinare + Unterlagen) sichern ab 7,40 EUR/Monat ++ Besser geht’s nicht!! ++