TM2 – Stabzweischlag: Verschiebung eines Knotens [Formel, Beispiel, Berechnung]

Wir betrachten in dieser Aufgabe den Stabzweischlag und berechnen mittels der Differentialgleichung des Stabs die Verschiebung des Knotens infolge der von außen angreifenden Kraft F.

Für ein optimales Verständnis hilft dir eine schrittweise Lösung der Aufgabe.

Dieser Lerntext ist ein Auszug aus unserem Onlinekurs TM2 – Festigkeitslehre.

Die in den vorangegangenen Lerneinheiten gezeigten Formeln zur Ermittlung der Spannungen und Verformungen an Stäben, können auch auf statisch bestimmte Stabwerke mit mehreren Stäben angewendet werden.

Merk’s dir!

Wir gehen dabei davon aus, dass nur infinitesimale Verformungen auftreten, so dass die Längenänderung der Stäbe $\triangle l$ und damit die Verschiebungen der Stäbe sehr klein sind. Damit können wir die Gleichgewichtsbedingungen am unverformten System aufstellen.

Wir gehen wie folgt vor:

Zunächst schneiden wir das System frei und tragen die wirkenden Kräfte ab.
Danach berechnen wir die Stabkräfte aus den Gleichgewichtsbedingungen am unverformten System.
Wir können dann die Längenänderung der Stäbe $\triangle l$ aus den berechneten Stabkräften berechnen.
Die Verschiebungen der Stäbe ermitteln wir zum Schluss grafisch mittels Trigonometrie.

Schauen wir uns mal ein Beispiel zum Stabzweischlag an.

Beispiel: Verschiebung bestimmen (Stabzweischlag)

Aufgabenstellung

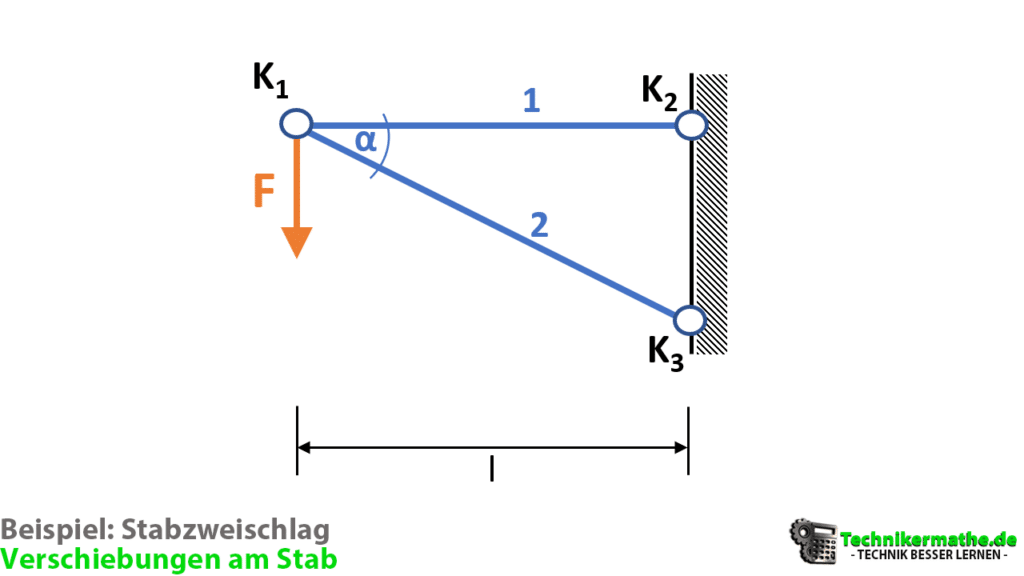
Stabzweischlag, Verschiebung, Stab, Verschiebung am Stab, Verschiebung berechnen, Verschiebungen am Stab — Beispiel: Stabzweischlag (Verschiebung bestimmen)

Gegeben sei der obige Stabzweischlag, an welchem die äußere Kraft F = 900 N angreift. Der Winkel zwischen den beiden Stäben betrage α = 35°, die Länge des Stabes S₁ beträgt l = 2m. Die Stäbe besitzen beide eine Querschnittsfläche von A = 80cm² auf. Das Elastizitätsmodul beider Stäbe betrage E = 210.000 N/mm².

a) Bestimme zunächst die Verschiebung des Knotens K₁ohne Zahlenwerte.

b) Berechne dann die Verschiebung mit den gegebenen Zahlenwerten!

Lösung a) Verschiebung des Knotens

Infolge der äußeren Kraft F, die vertikal am Knoten K₁ angreift, verschiebt sich dieser. Unsere Aufgabe ist es nun, diese Verschiebung zu berechnen. Dazu schneiden wir das System zunächst am Knoten K₁ frei und tragen die dort wirkenden Kräfte ab.

Freischnitt

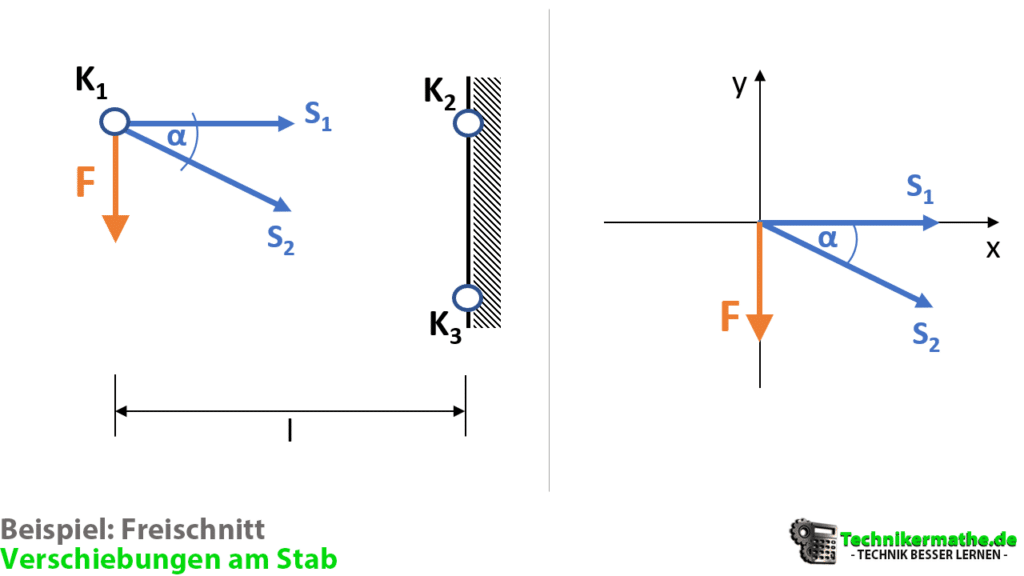
Wir haben den Knoten K₁ freigeschnitten und die beiden Stabkräfte S₁ und S₂ als Zugkräfte angenommen. Außerdem greift noch die äußere Kraft F am Knoten K₁ an. Zur Aufstellung der Gleichgewichtsbedingungen kann man die drei Kräfte in ein Koordinatensystem übernehmen. Zur Aufstellung der Gleichgewichtsbedingung in x-Richtung und in y-Richtung müssen wir alle Kräfte, die in die x,y-Ebene wirken, also einen Winkel zur Horizontalen bzw. Vertikalen aufweisen in x- und y-Komponenten zerlegen.

Für unser Beispiel ist der Stab S₂ ein schräger Stab, der in die x,y-Ebene wirkt. Für diesen Stab müssen wir eine Kräftezerlegung vornehmen, um die x- und y-Komponente zu bestimmen:

Kräftezerlegung, Stabzweischlag, Stab, Verschiebung, Verschiebung am Stab — Kräftezerlegung einer Stabkraft

In der obigen Grafik ist die Kräftezerlegung des Stabs S₂ zu sehen. Da der Winkel $\alpha$ zur x-Achse gegeben ist, wird die x-Komponente mit dem Kosinus und die y-Komponente mit dem Sinus berechnet. Betrachten wir in der folgenden Grafik alle wirkenden Kräfte im Knoten K₁:

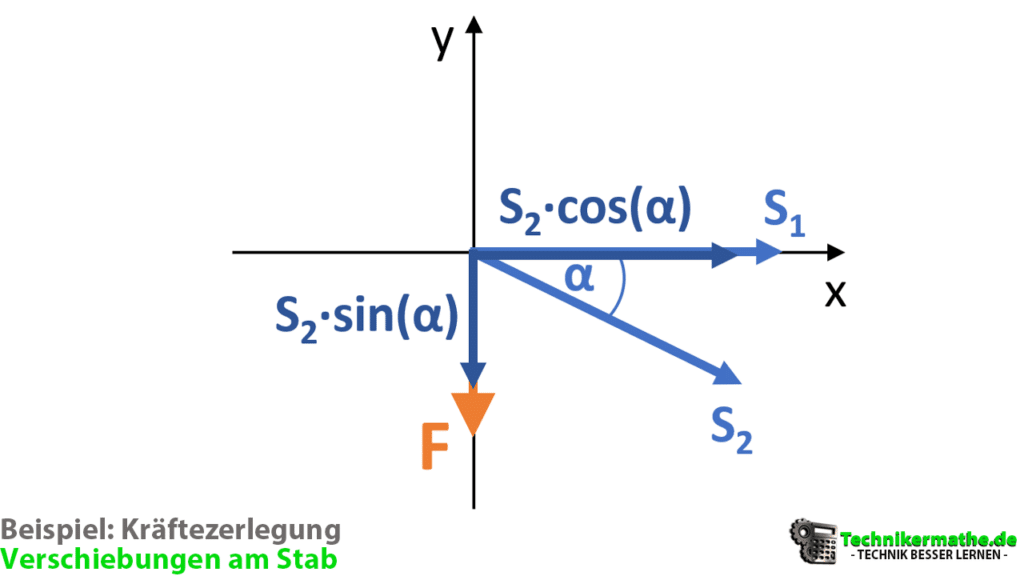
Verschiebung, Stab, Stabzweischlag, Kräftezerlegung, Stabkräfte, äußere Kraft, Verschiebungen im Stab — Koordinatensystem mit Stabkräften und äußerer Kraft

Im nächsten Schritt können wir die Gleichgewichtsbedingungen aufstellen, um die unbekannten Stabkräfte S₁ und S₂ zu berechnen. Diese stellen wir am unverformten System auf, da wir von infinitesimalen Verformungen ausgehen. Das bedeutet, dass wir bei der Aufstellung der Gleichgewichtsbedingungen die Verschiebung des Knotens K₁ infolge der äußeren Kraft F zunächst vernachlässigen.

Gleichgewichtsbedingungen am unverformten System

Wir stellen zunächst die Gleichgewichtsbedingung in x-Richtung auf.

Die Summe aller horizontalen Kräfte muss Null ergeben:

$\rightarrow: \; \sum F_x = 0$

Wir betrachten alle horizontalen Kräfte. Alle Kräfte die in Richtung der positiven x-Achse zeigen, werden positiv berücksichtigt. Alle Kräfte, die in negative x-Richtung zeigen, werden negativ berücksichtigt.

$\rightarrow: S_2 \cdot \cos(\alpha) + S_1 = 0$

Aus dieser Gleichgewichtsbedingung können wir noch keine unbekannte Stabkraft berechnen.

Wir stellen als nächstes die Gleichgewichtsbedingung in y-Richtung auf.

Die Summe aller vertikalen Kräfte muss Null ergeben:

$\uparrow \; \sum F_y = 0$

Wir betrachten alle vertikalen Kräfte. Alle Kräfte die in Richtung der positiven y-Achse zeigen, werden positiv berücksichtigt. Alle Kräfte, die in negative y-Richtung zeigen, werden negativ berücksichtigt.

$\uparrow: -S_2 \cdot \sin(\alpha) - F = 0$

Wir können hier die unbekannte Stabkraft S₂ bestimmen, indem wir nach dieser auflösen:

$S_2 = -\frac{F}{\sin(\alpha)}$

Nachdem wir aus der Gleichgewichtsbedingung in y-Richtung die unbekannte Stabkraft S₂ berechnen können (bei gegebenem F), können wir aus der Gleichgewichtsbedingung in x-Richtung die unbekannte Stabkraft S₁ berechnen.

$\rightarrow: S_2 \cdot \cos(\alpha) + S_1 = 0$

Auflösen nach S₁:

$S_1 = -S_2 \cdot \cos(\alpha)$

Einsetzen von S₂ aus der Gleichgewichtsbedingung in y-Richtung:

$S_1 = -(-\frac{F}{\sin(\alpha)}) \cdot \cos(\alpha)$

$S_1 = \frac{F \cdot \cos(\alpha)}{\sin(\alpha)}$

Merk’s dir!

Trigonometrische Umformung:

$\tan(\alpha) = \frac{\sin(\alpha)}{\cos(\alpha)}$

Und damit:

$\frac{1}{\tan(\alpha)} = \frac{\cos(\alpha)}{\sin(\alpha)}$

Mit der trigonometrischen Umformung erhalten wir:

$S_1 = \frac{F}{\tan(\alpha)}$

Wir erhalten also die folgenden Stabkräfte:

$S_2 = -\frac{F}{\sin(\alpha)}$ Druckstab

$S_1 = \frac{F}{\tan(\alpha)}$ Zugstab

Merk’s dir!

Der Stab S₂ ist ein Druckstab, da er negativ ist. Das bedeutet, dass die von uns zuvor angenommene Richtung (Zugstab) genau entgegengesetzt wirkt. Der Stab S₁ ist positiv. Damit ist die von uns angenommene Richtung (Zugstab) korrekt.

Nachdem wir die Stabkräfte berechnet haben, können wir als nächstes die Längenänderung der Stäbe berechnen, die infolge der äußeren Kraft F auftreten.

Längenänderung der Stäbe berechnen

Die Längenänderung eines Stabes können wir aus dem Elastizitätsgesetz für einen Stab (Lerneinheit: Differentialgleichung der Verschiebung) bestimmen:

$u' = \frac{N}{E \cdot A} + \alpha \cdot \Delta T$

Da wir hier keine Temperaturunterschiede gegeben haben, gilt $\Delta T = 0$ :

$u' = \frac{N}{E \cdot A}$

Zur Bestimmung der Verschiebung u, müssen wir die Gleichung einmal über die Stablänge l integrieren:

$\int_0^{x =l} u' dx = \int_0^{x = l} \frac{N}{E \cdot A} \; dx$

$u(l) - u(0) = \frac{N}{E \cdot A} \cdot l$

$\Delta l = u(l) - u(0)$

$\Delta l = \frac{N}{E \cdot A} \cdot l$

Anstelle von $N$ treten die Stabkräfte $S_1$ und $S_2$ .

Für den Stab S₁ gilt:

$\Delta l_1 = \frac{S_1}{EA} \cdot l_1 = \frac{F \cdot l_1}{EA \cdot \tan (\alpha)}$

Der Stab $S_1$ hat die Länge l₁ = l:

$\Delta l_1 = \frac{F \cdot l}{EA \cdot \tan (\alpha)}$ Längenänderung Stab S₁

Die Längenänderung des Stabes S₁ ist positiv. Damit verlängert sich der Stab.

Für den Stab S₂ gilt:

$\Delta l_2 = \frac{S_2}{EA} \cdot l_2$

Die Länge des Stabs $S_2$ können wir über die Trigonometrie am rechtwinkligen Dreieck berechnen:

Verschiebung, Stab, Verlängerung deines Stabes, Verschiebung, Trigonometrie, Längenänderung, Kosinus, Trigonometrie, Stabkräfte — Trigonometrie anwenden

Wir können also aus der gegebenen Geometrie die Länge l₂ berechnen:

$\cos(\alpha) = \frac{l_1}{l_2}$

$l_2 = \frac{l_1}{\cos(\alpha)}$

Mit l = l₁:

$l_2 = \frac{l}{\cos(\alpha)}$

Einsetzen in die Längenänderung des Stabes S₂:

$\Delta l_2 = \frac{S_2}{EA} \cdot l_2 = -\frac{F \cdot l_2}{EA \sin (\alpha) \cos (\alpha)}$

Die Längenänderung des Stabs S₂ ist negativ. Damit verkürzt sich der Stab.

Verschiebung bestimmen

Wir können als nächstes die Verschiebung des Knotens K₁ bestimmen. Dazu zeichnen wir die Längenänderungen ein. Den Stab S₁ verlängern wir, den Stab S₂ verkürzen wir:

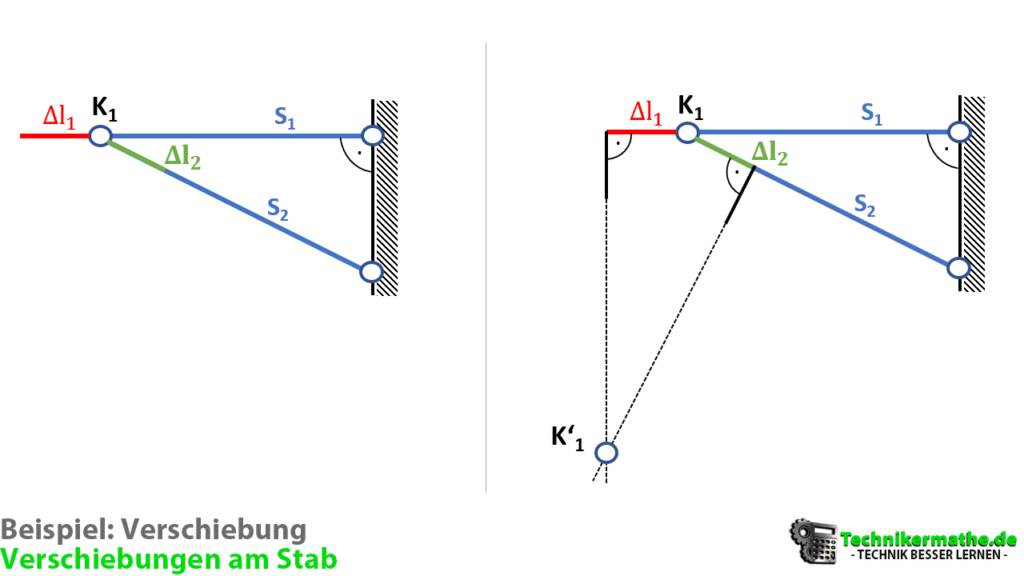
Verschiebung, Stab, Knoten, Verschiebung des Knotens, Stabzweischlag, Längenänderung — Verschiebung des Knotens

In der obigen Grafik haben wir den Stab S₁ verlängert um $\Delta l_1$ und den Stab S₂ verkürzt um $\Delta l_2$ eingezeichnet. Danach haben wir von dem verlängerten Stab S₁ und dem verkürzten Stab S₂ eine dazu orthogonale Linie (im 90°-Winkel) gezogen. Dort, wo sie sich diese beiden Linien treffen, liegt der neue Knoten K’2, der sich infolge der angreifenden Kraft F ergibt.

Die Längenänderungen wurden innerhalb der Grafik sehr groß eingezeichnet, so dass sich die neue Lage des Knotens K’2 ist in der Grafik sehr weit entfernt vom ursprünglichen Knoten ergibt. Das dient dazu, die Verschiebung besser veranschaulichen können. Die tatsächliche Verschiebung des Knotens ist sehr klein und wäre damit kaum sichtbar. Da wir in einem nächsten Schritt aber die Geometrie benötigen, ist es sinnvoll die Verschiebungen innerhalb der Skizze groß zu wählen.

Wir zeichnen ausgehend von der ursprünglichen Lage des Knotens K₁ die horizontale Verschiebung u und die vertikale Verschiebung v ein:

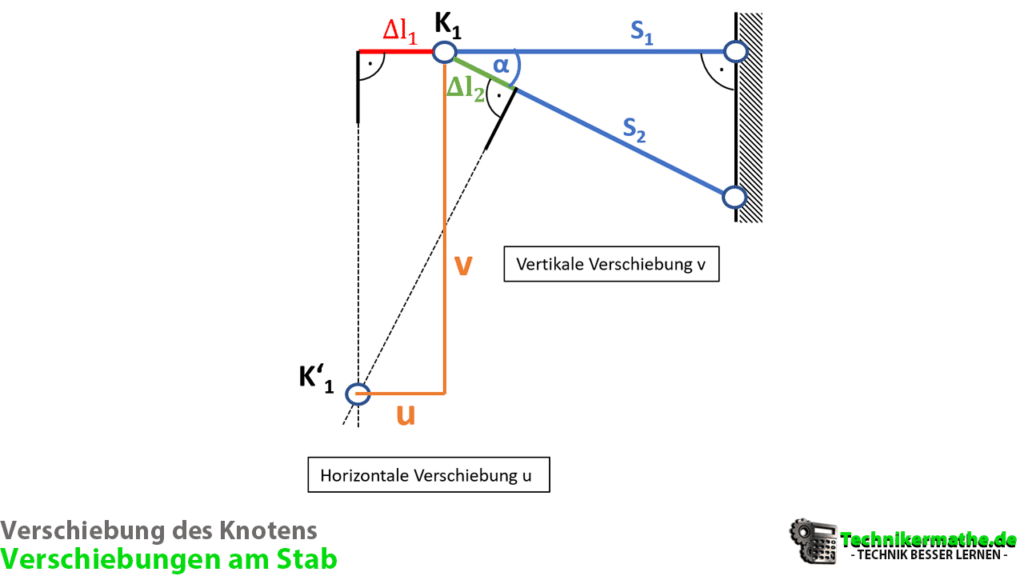
Verschiebung, Knoten, Stabzweischlag, Festigkeitslehre, Verschiebung des Knotens, horizontale Verschiebung, vertikale Verschiebung — Horizontale und vertikale Verschiebung

Wir zeichnen die Verschiebung des Knotens K1 nach K₁‘ in vertikale Richtung (v) und in horizontale Richtung (u) ein. Wir sehen, dass die horizontale Verschiebung u der Längenänderung Δl₁ entspricht:

$u = \Delta l_1 = \frac{F \cdot l}{EA \cdot \tan (\alpha)}$ Horizontale Verschiebung

Die Verschiebung in vertikale Richtung v müssen wir hingegen zunächst berechnen. Das können wir mittels Trigonometrie am rechtwinkligen Dreieck:

Stabzweischlag, Verschiebung, Knoten, Verschiebung des Knotens, Verschiebungen am Stab — Vertikale Verschiebung bestimmen

Wir haben oben rechts und unten rechts ein rechtwinkliges Dreieck gegeben und kennen den Winkel α, die Längenänderung Δl₂sowie die Verschiebung u = Δl₁. Damit können wir die Verschiebung u ganz leicht berechnen, indem wir die Trigonometrie am rechtwinkligen Dreieck für beide Dreiecke anwenden und dann daraus die Verschiebung v berechnen:

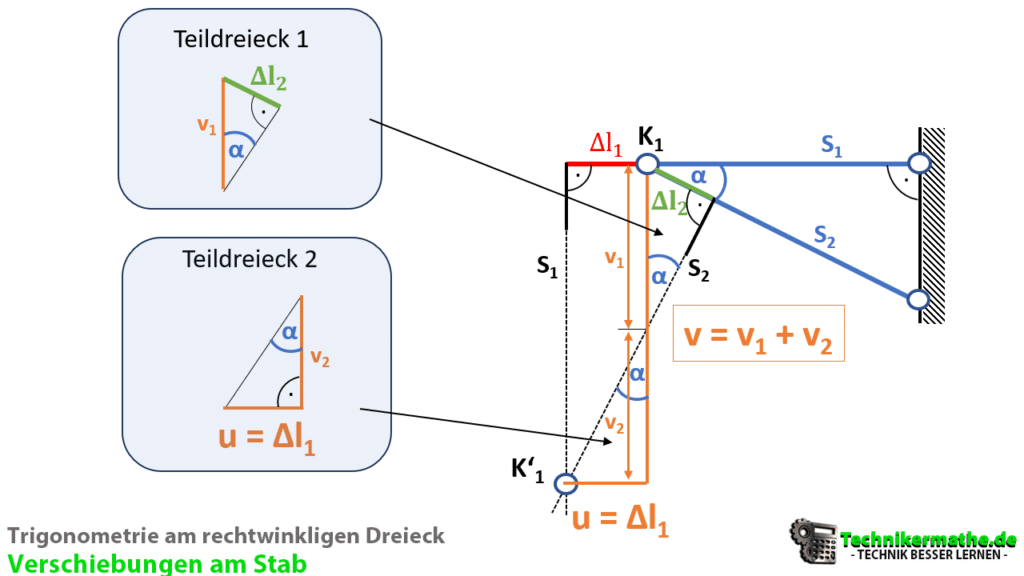
Stabzweischlag, Festigkeitslehre, Stab, Verschiebung, Knoten, vertikale Verschiebung — Vertikale Verschiebung bestimmen

Wir sehen die beiden rechtwinkligen Teildreiecke. Wir benötigen beide Dreiecke, um die gesamte Verschiebung u zu berechnen.

1.Teildreieck

Wir berechnen zunächst v₁ für das erste Teildreieck. Gegeben haben wir hier den Winkel α sowie die Verschiebung Δl₂. v₁ ist hier die Hypotenuse, da sie gegenüber vom rechten Winkel liegt. Die gegebene Seite Δl₂ ist die Gegenkathete, weil sie gegenüber vom Winkel α liegt. Demnach wählen wir hier den Sinus:

$\sin(\alpha) = \frac{\text{Gegenkathete}}{\text{Hypotenuse}}$

$\sin(\alpha) = \frac{|\Delta l_2|}{v_1}$

Die Längenänderung wird in Betragsstriche gesetzt, da wir die Längen hier addieren müssen, damit wir die gesamte Verschiebung v ermitteln können.

Wir lösen nach v₁ auf:

$v_1 = \frac{|\Delta l_2|}{\sin(\alpha)}$

2. Teildreieck

Wir berechnen v₂ für das zweite Teildreieck. Gegeben haben wir hier den Winkel α sowie die Verschiebung u, welche der Längenänderung Δl₁ entspricht. v₂ ist hier die Ankathete, da sie an dem Winkel α liegt. Die gegebene Seite Δl₁ ist die Gegenkathete, weil sie gegenüber vom Winkel α liegt. Demnach wählen wir hier den Tangens:

$\tan(\alpha) = \frac{\text{Gegenkathete}}{\text{Ankathete}}$

$\tan(\alpha) = \frac{|\Delta l_1|}{v_2}$

Die Längenänderung wird in Betragsstriche gesetzt, da wir die Längen hier addieren müssen, damit wir die gesamte Verschiebung v ermitteln können.

Wir lösen nach v₂ auf:

$v_2 = \frac{|\Delta l_1|}{\tan(\alpha)}$

Wir können als nächstes die gesamte Verschiebung v berechnen, indem wir die beiden Verschiebungen addieren:

$v = v_1 + v_2 = \frac{|\Delta l_2|}{\sin(\alpha)} + \frac{|\Delta l_1|}{\tan(\alpha)}$

Da wir die Längenänderung bereits berechnet haben, können wir diese nun einsetzen:

$v = v_1 + v_2 = \frac{|-\frac{F \cdot l_2}{EA \sin (\alpha) \cos (\alpha)}|}{\sin(\alpha)} + \frac{|\frac{F \cdot l}{EA \cdot \tan (\alpha)}|}{\tan(\alpha)}$

$v = \frac{F \cdot l_2}{EA \sin (\alpha)^2 \cos (\alpha)} + \frac{F \cdot l}{EA \cdot \tan^2 (\alpha)}$ Vertikale Verschiebung

Wir haben die Gleichungen zur Bestimmung der Verschiebung des Knotens bestimmt.

Lösung b) Verschiebung in Zahlenwerten

Nachdem wir die Gleichungen ermittelt haben, um die Verschiebung des Knotens zu berechnen, können wir als nächstes die Zahlenwerte aus der Aufgabenstellung einsetzen:

Horizontale Verschiebung:

$u = \Delta l_1 = \frac{F \cdot l}{EA \cdot \tan (\alpha)}$

Wir haben das Elastizitätsmodul in N/mm² gegeben, die Querschnittsfläche in cm² und die Länge in m. Wir müssen uns auf eine Einheit einigen (m, cm, mm). Wir wählen hier mm, da die Umrechnung der Länge und der Fläche sehr einfach ist:

$A = 80cm^2 = 80 \cdot 100 mm^2 = 8.000 mm^2$

$l = 2m = 2 \cdot 10 \cdot 10 \cdot 10 = 2.000 mm$

Wir können nun alle Werte einsetzen:

$u = \frac{900 N \cdot 2.000mm}{210.000 \frac{N}{mm^2} \cdot 8.000 mm^2 \cdot \tan (35^{\circ})}$

$u = 0,00153mm$

Die Verschiebung des Knotens aufgrund der äußeren Belastung in horizontaler Richtung erfolgt um 0,00153mm.

Vertikale Verschiebung:

$v = \frac{F \cdot l_2}{EA \sin^2 (\alpha) \cos (\alpha)} + \frac{F \cdot l}{EA \cdot \tan^2 (\alpha)}$

Für die Länge l₂ gilt (siehe weiter oben):

$l_2 = \frac{l}{\cos(\alpha)} = \frac{2.000mm}{\cos(35^{\circ})} = 2.441,55mm$

Wir setzen alle gegebenen Werte ein:

$v = \frac{900 N \cdot 2.441,55mm}{210.000 \frac{N}{mm^2} \cdot 8.000 mm^2 \sin^2 (35^{\circ}) \cos (35^{\circ})} + \frac{900 N \cdot 2.000mm}{210.000 \frac{N}{mm^2} \cdot 8.000 mm^2 \cdot \tan^2 (35^{\circ})}$

$v = 0,007mm$

Die Verschiebung des Knotens aufgrund der äußeren Belastung in vertikaler Richtung erfolgt um 0,007mm.

Anhand der Ergebnisse ist deutlich zu erkennen, dass die Verschiebung sehr klein ist. Innerhalb der Skizze hingegen wirkt die Verschiebung sehr groß. Die Verschiebung innerhalb der Skizze wurde deswegen so groß gewählt, damit die Berechnung der Verschiebung mittels Trigonometrie sichtbar wird. Je größer die eingezeichnete Verschiebung, desto einfach ist es anhand der Skizze die Berechnungen vorzunehmen.

Was gibt es noch bei uns?

Optimaler Lernerfolg durch tausende Übungsaufgaben

Übungsbereich (Demo) - Lerne mit mehr als 4000 Übungsaufgaben für deine Prüfungen

Quizfrage 1

“Wusstest du, dass unter jedem Kursabschnitt eine Vielzahl von verschiedenen interaktiven Übungsaufgaben bereitsteht, mit denen du deinen aktuellen Wissensstand überprüfen kannst?”

Alle Technikerschulen im Überblick

Zum Verzeichnis der Technikerschulen (Alles Rund um die Schulen) — Zum Verzeichnis der Technikerschulen

Kennst du eigentlich schon unser großes Technikerschulen-Verzeichnis für alle Bundesländer mit allen wichtigen Informationen (Studiengänge, Kosten, Anschrift, Routenplaner, Social-Media) ? Nein? – Dann schau einfach mal hinein:

Was ist Technikermathe?

Unser Dozent Jan erklärt es dir in nur 2 Minuten!

Oder direkt den > kostenlosen Probekurs < durchstöbern? – Hier findest du Auszüge aus Alle Onlinekurse Technikermathe!

Geballtes Wissen in derzeit 26 Kursen

Hat dir dieses Thema gefallen? – Ja? – Dann schaue dir auch gleich die anderen Themen zu den Kursen

WT3 (Werkstoffprüfung) und
TM1 (Technische Mechanik – Statik) an.

Lerne nun erfolgreich mit unserem Onlinekurs Technische Mechanik 1 — TM1 (Technische Mechanik)

Lerne nun erfolgreich mit unserem Onlinekurs Werkstofftechnik 3 — WT3 (Werkstoffprüfung)

Perfekte Prüfungsvorbereitung für nur 14,90 EUR/Jahr pro Kurs

++ Günstiger geht’s nicht!! ++

Oder direkt Mitglied werden und Alle unsere Onlinekurse (inkl. Webinare + Unterlagen) sichern ab 7,40 EUR/Monat ++ Besser geht’s nicht!! ++