TM2 – Prüfungsaufgabe: Schubspannungen bei Querkraftbiegung (dreieckige Fläche)

In dieser Lerneinheit betrachten wir eine Aufgabe mit ausführlicher Lösung zur Berechnung der Schubspannungen, wenn äußere Querkräfte an einen Balken mit dreieckiger Querschnittsfläche angreifen.

In dieser Lerneinheit wollen wir uns anschauen, wie die Schubspannungen berechnet werden, wenn Querkraftbiegung gegeben ist. Dabei betrachten wir einen Balken mit einer dreieckigen Querschnittsfläche.

Für ein optimales Verständnis helfen dir drei ausführliche Videoclips und zwei anschauliche Rechenbeispiele zu dem Thema.

Dieser Lerntext ist ein Auszug aus unserem Onlinekurs TM2 – Festigkeitslehre.

Wir wollen in dieser Lerneinheit

die Auflagerkräfte,
das statische Moment einer dreieckigen Fläche,
die Querkraft,
das Flächenträgheitsmoment einer dreieckigen Fläche,
den Schubspannungsverlauf sowie
die maximale Schubspannung berechnen.

Prüfungsaufgabe: Schubspannungen bei Querkraftbiegung

Aufgabenstellung

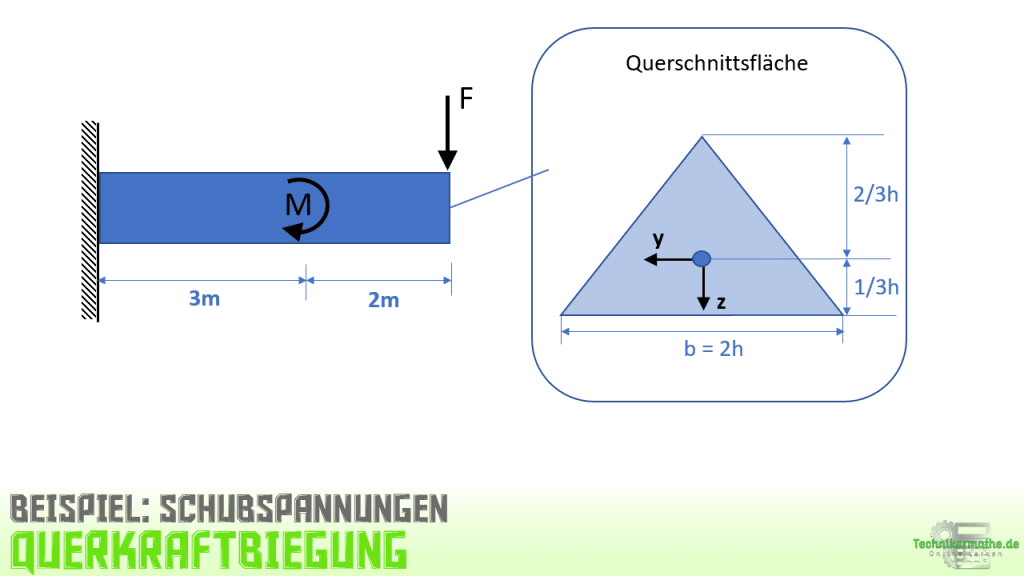
Schubspannungen bei Querkraftbiegung, Schubspannungen, Querkraft, Balken, dreieckige Fläche, dreieckige Querschnittsfläche, Feste Einspannung — Beispiel: Balken mit äußerer Querkraft

In der obigen Grafik siehst du einen Balken, welcher an der linken Seite fest eingespannt ist. Der Balken wird durch eine äußere Querkraft F = 400 N belastet (Querkraftbiegung) und zusätzlich durch ein äußeres Moment M = 250 Nm. Der Querschnitt des Balkens ist ein gleichschenkliges Dreieck mit h = 0,4m.

a) Berechne die Auflagerkräfte!

b) Bestimme das statische Moment!

c) Bestimme den Schubspannungsverlauf im Querschnitt für das Ende des Balkens (Kraftangriffspunkt)!

d) Bestimme die maximale Schubspannung!

Auflagerkräfte berechnen

Zunächst berechnen wir die Auflagerkräfte an der festen Einspannung. Dazu müssen wir den Balken zunächst von seinen Auflagern trennen, also freischneiden:

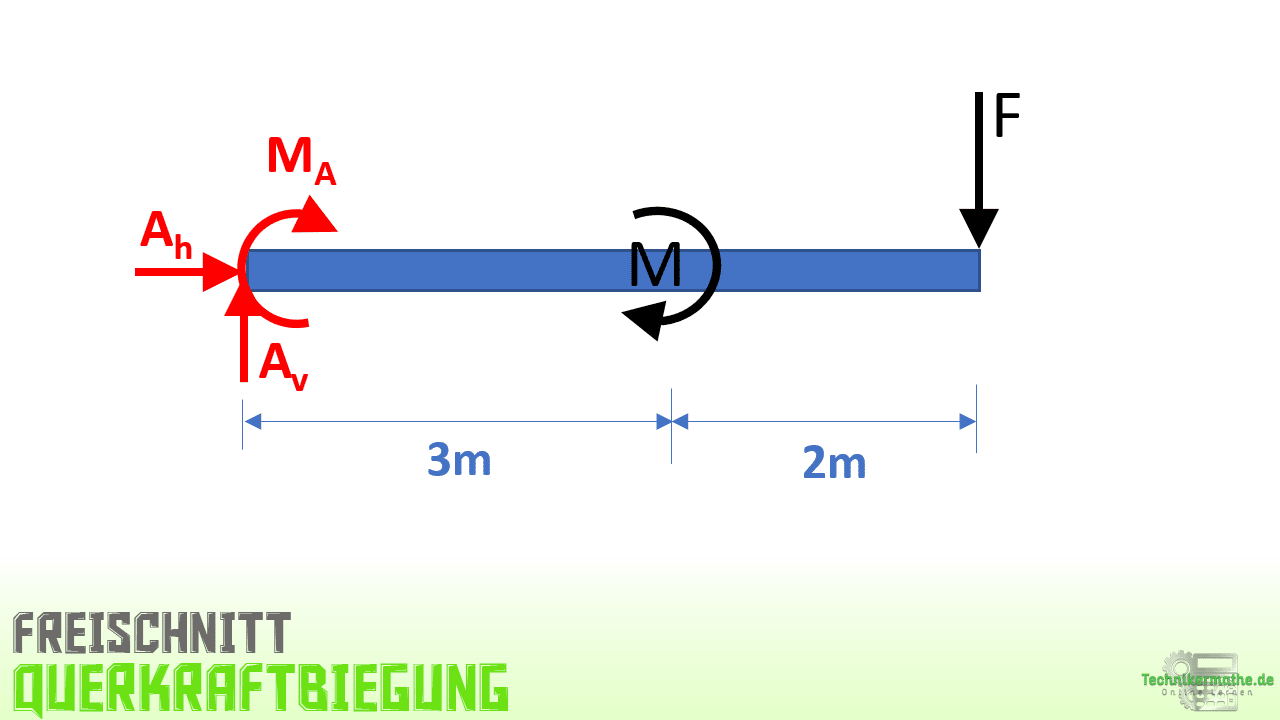
Auflagerkräfte, Schubspannungen bei Querkraftbiegung, Schubspannungen, Balken, Querkraft, Einspannung, Moment, Lagerkräfte — Auflagerreaktionen der festen Einspannung (Freischnitt)

Eine feste Einspannung überträgt insgesamt 3 Lagerreaktionen. Eine horizontale und eine vertikale Lagerkraft sowie ein Moment. In welche Richtung die horizontale Lagerkraft A_h (links/rechts) bzw. die vertikale Lagerkraft Av (oben/unten) angenommen werden, ist frei wählbar. Das selbe gilt für die Drehrichtung des Einspannmoments M_A(rechtsdrehend/linksdrehend). Ist das Ergebnis gleich positiv, so stimmt die Richtung. Bei einem negativen Ergebnis wirkt die Kraft/Moment genau entgegengesetzt.

Horizontale Auflagerkraft

Wir starten mit Berechnung der horizontalen Auflagerkraft aus der horizontalen Gleichgewichtsbedingung:

$\sum F_{ix} = 0$

Die Summe aller horizontalen Kräfte (äußere Kräfte sowie Lagerkräfte) muss Null ergeben. Wir haben nur die Auflagerkraft A_h gegeben:

$A_h = 0$

Die Auflagerkraft A_h ist Null, weil keine äußeren horizontalen Kräfte an den Balken angreifen.

Vertikale Auflagerkraft

Als nächstes berechnen wir die vertikale Auflagerkraft aus der vertikalen Gleichgewichtsbedingung:

$\sum F_{iy} = 0$

Die Summe aller vertikalen Kräfte (äußere Kräfte sowie Lagerkräfte) muss Null ergeben. Vorzeichenkonvention: Alle nach oben zeigenden Kräfte werden positiv, alle nach unten zeigenden Kräfte negativ berücksichtigt.

$A_v - F = 0$

$A_v = F$

$A_v = 400 N$

Die Auflagerkraft A_v muss 400 betragen, damit sich der Balken vertikal nicht verschiebt. Da wir ein positives Ergebnis erhalten, ist die angenommene Richtung (nach oben wirkend) richtig.

Einspannmoment

Zuletzt berechnen wir das Einspannmoment aus der Momentengleichgewichtsbedingung:

$\sum M = 0$

Die Summe aller Momente muss Null ergeben. Vorzeichenkonvention: Alle linksdrehenden Momente werden positiv, alle rechtsdrehenden Momente negativ berücksichtigt.

Zunächst müssen wir einen Bezugspunkt festlegen. Wir können hier frei wählen, da nur noch das Einspannmoment als Unbekannte gegeben ist. Wir wählen beliebig das Lager A.

$\sum M^A = 0$

Alle Kräfte, deren Wirkungslinie den Bezugspunkt schneiden, werden nicht berücksichtigt. Diese Kräfte weisen keinen Hebelarm (senkrechten Abstand) zum Bezugspunkt auf und üben demnach kein Moment auf das Lager A aus. Hierunter fallen die beiden Auflagerkräfte A_v und A_h. Momente werden immer berücksichtigt, auch wenn diese im Bezugspunkt liegen.

$-M_A - M - F \cdot 5m = 0$

$M_A = -M - F \cdot 5m$

$M_A = -250 Nm - 400 N \cdot 5m$

$M_A = -2.250 Nm$

Das Einspannmoment M_A muss -2.250Nm betragen, damit sich der Balken nicht dreht. Da wir ein negatives Ergebnis erhalten, ist die angenommene Richtung (rechtsdrehend) nicht richtig. Tatsächlich ist das Einspannmoment ein linksdrehendes Moment.

Es gibt nun zwei Möglichkeiten:

Wir lassen das Einspannmoment als rechtsdrehendes Moment stehen und rechnen mit dem negativen Wert weiter.
Wir tragen das Einspannmoment als linksdrehendes Moment ab und rechnen mit dem positiven Wert weiter.

Wir entscheiden uns hier für Variante a.

Statisches Moment bestimmen

Im nächsten Schritt berechnen wir das statische Moment, welches wir später bei der Berechnung der Schubspannung benötigen.

Das statische Moment in Bezug auf die y-Achse des Querschnitts wird wie folgt berechnet:

$S_y = \int z \cdot dA$

In der obigen Grafik haben wir eine dreieckige Querschnittsfläche gegeben. Wir wollen uns anschauen, wie in einem solchen Fall das statische Moment berechnet wird. Die Lage des Schwerpunkts des Profils ist ebenfalls angegeben. Sollte die Lage nicht angegeben sein, so müsst ihre diese zusätzlich ermitteln (Tabellenwerke!).

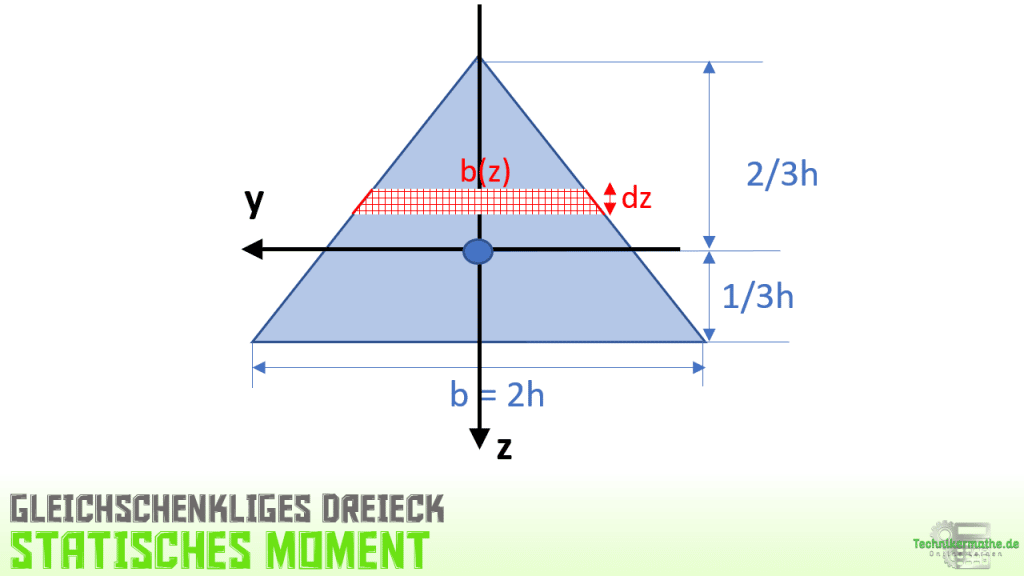
Statisches Moment, Dreieck, Integration, Schubspannungen, dreieckige Fläche, dreieckige Querschnittsfläche — Statisches Moment (dreieckiger Fläche)

Wir gehen für jede Teilfläche vor, wie es in der vorangegangenen Lerneinheit beschrieben ist. Wir wählen also einen infinitesimalen Streifen dA mit der Breite b(z) und der Höhe dz. Wir setzen $dA = b(z) \cdot dz$ in die obige Gleichung ein:

(1) $S_y = \int_{z}^{1/3h} z \cdot b(z) \cdot dz$ Statisches Moment

Die Integralgrenzen laufen immer von z bis zum Maximum von z. Das Maximum von z ist z = 1/3h.

Die Breite b(z) ändert sich beim Dreieck in z-Richtung. Deswegen müssen wir die Breite zunächst bestimmen. Wir betrachten dazu einen Schenkel des Dreiecks und legen diesen in das gegebene y,z-Koordinatensystem:

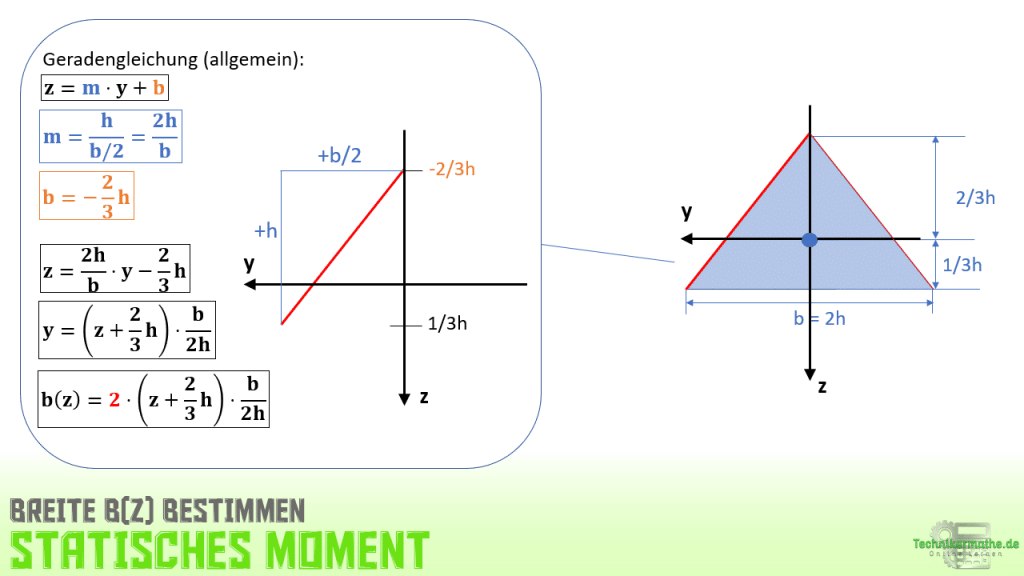
Statisches Moment, Dreieck, Geradengleichung, Breite, Schubspannungen, Balken — Statisches Moment (dreieckige Fläche)

Wir legen den linken Schenkel in das Koordinatensystem und stellen die allgemeine Geradengleichung auf. Zunächst berechnen wir nun die Geradengleichung z = my+b bzw. h(y) = my+b. Wir berechnen also die Änderung der Höhe in Abhängigkeit von der y-Achse.

Dazu müssen wir zunächst die Steigung m bestimmen. Wir starten dazu an einem Ende des Schenkels und bewegen uns in y- und z-Richtung zum anderen Ende des Schenkels. Dabei müssen wir immer darauf achten, ob wir uns in negative oder positive Achsenrichtung bewegen. Wir bewegen uns vom obere Ende des Schenkels zum unteren, indem wir b/2-Schritte in positive y-Richtung und h-Schritte in positive z-Richtung gehen. Damit sind beide Koordinaten positiv zu berücksichtigen.

$m = \dfrac{\text{Schritte in z-Richtung}}{\text{Schritte in y-Richtung}}$

$m = \dfrac{h}{b/2} = \dfrac{2h}{b}$

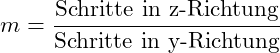
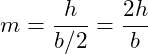
Als nächstes benötigen wir noch die Variable b, also den Schnitt der Funktion (des Schenkels) mit der y-Achse:

$b = -\dfrac{2}{3}h$

Wir können die ermittelten Werte in die Geradengleichung eingeben:

$z = m \cdot y + b$

$z = \dfrac{2h}{b} \cdot y - \dfrac{2}{3}h$

Das ist die Änderung der Höhe in Abhängigkeit von der Variable y.

Wir suchen nun aber die Änderung der Breite in Abhängigkeit von der Variable z, weshalb wir die Gleichung nach z auflösen:

$y = (z + \dfrac{2}{3}h) \cdot \dfrac{b}{2h}$

Wir haben hier nun zwei Schenkel gegeben, die beide dafür sorgen, dass die Breite sich über die z-Achse ändert. Wir berücksichtigen den zweiten Schenkel, indem wir die Gleichung mit 2 multiplizieren:

$b(z) = 2 \cdot (z + \dfrac{2}{3}h) \cdot \dfrac{b}{2h}$

$b(z) = 2 \cdot \dfrac{b}{2h} \cdot z + 2 \cdot \dfrac{2}{3}h \cdot \dfrac{b}{2h}$

$b(z) = \dfrac{b}{h} \cdot z + \dfrac{2}{3} b$ Breite des infinitesimalen Streifens

Als nächstes setzen wir b(z) in die obige Gleichung (1) ein:

(1) $S_y = \int_{z}^{1/3h} z \cdot (\dfrac{b}{h} \cdot z + \dfrac{2}{3} b) \cdot dz$

$S_y = \int_{z}^{1/3h} (\dfrac{b}{h} \cdot z^2 + \dfrac{2}{3} b \cdot z) \cdot dz$

Wir integrieren:

$S_y = [\dfrac{b}{h} \cdot \dfrac{1}{3} z^3 + \dfrac{2}{3} b \cdot \dfrac{1}{2} z^2]_{z}^{1/3h}$

$S_y = [\dfrac{1}{3}\dfrac{b}{h} \cdot z^3 + \dfrac{1}{3} b \cdot z^2]_{z}^{1/3h}$

Einsetzen der Grenzen:

$S_y = \dfrac{1}{3}\dfrac{b}{h} \cdot (\dfrac{1}{3}h)^3 + \dfrac{1}{3} b \cdot (\dfrac{1}{3}h)^2 - (\dfrac{1}{3}\dfrac{b}{h} \cdot z^3 + \dfrac{1}{3} b \cdot z^2)$

$S_y = \dfrac{1}{3}\dfrac{b}{h} \cdot (\dfrac{1}{3}h)^3 + \dfrac{1}{3} b \cdot (\dfrac{1}{3}h)^2 - \dfrac{1}{3}\dfrac{b}{h} \cdot z^3 - \dfrac{1}{3} b \cdot z^2$

$S_y = \dfrac{1}{81}bh^2 + \dfrac{1}{27}bh^2 - \dfrac{1}{3}\dfrac{b}{h} \cdot z^3 - \dfrac{1}{3} b \cdot z^2$

$S_y = \dfrac{4}{81}bh^2 - \dfrac{1}{3}\dfrac{b}{h} \cdot z^3 - \dfrac{1}{3} b \cdot z^2$

Laut Aufgabenstellung ist b = 2h:

$S_y = \dfrac{4}{81} \cdot 2h \cdot h^2 - \dfrac{1}{3} \cdot \dfrac{2h}{h} \cdot z^3 - \dfrac{1}{3} \cdot 2h \cdot z^2$

$S_y = \dfrac{8}{81} \cdot h^3 - \dfrac{2}{3} \cdot z^3 - \dfrac{2}{3} \cdot h \cdot z^2$

Einsetzen von h = 0,4m:

$S_y = 0,0063m^3 - \dfrac{2}{3} \cdot z^3 - 0,2667m \cdot z^2$

Wir haben das statische Moment in Abhängigkeit von z bestimmt.

Schubspannungsverlauf

Wir können nun den Verlauf der Schubspannungen bei Querkraftbiegung mittels der folgenden Formel bestimmen:

$\tau(z) = \dfrac{Q \cdot S_y}{I_y \cdot b(z)}$

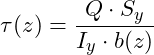
Hierbei ist Q die Querkraft, S_y das statische Moment, I_y das Flächenträgheitsmoment und b(z) die Breite in Abhängigkeit von z.

Querkraft

Wir haben in der Aufgabenstellung angegeben, dass die Schubspannungen für das Ende des Balkens bestimmt werden soll, also dort wo die äußere Kraft F angreift. Wir müssen also zunächst die Querkraft Q in diesem Schnittbereich berechnen. Dazu schneiden wir den Balken im relevanten Bereich:

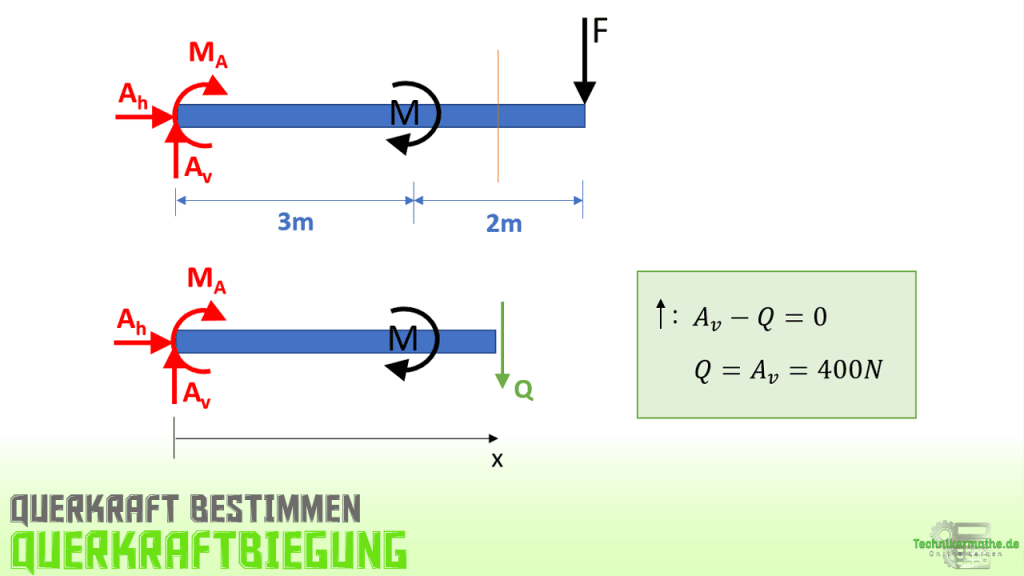
Die Querkraft beträgt also:

$Q = 400 N$

Flächenträgheitsmoment

Als nächstes benötigen wir noch das Flächenträgheitsmoment für ein gleichschenkliges Dreieck:

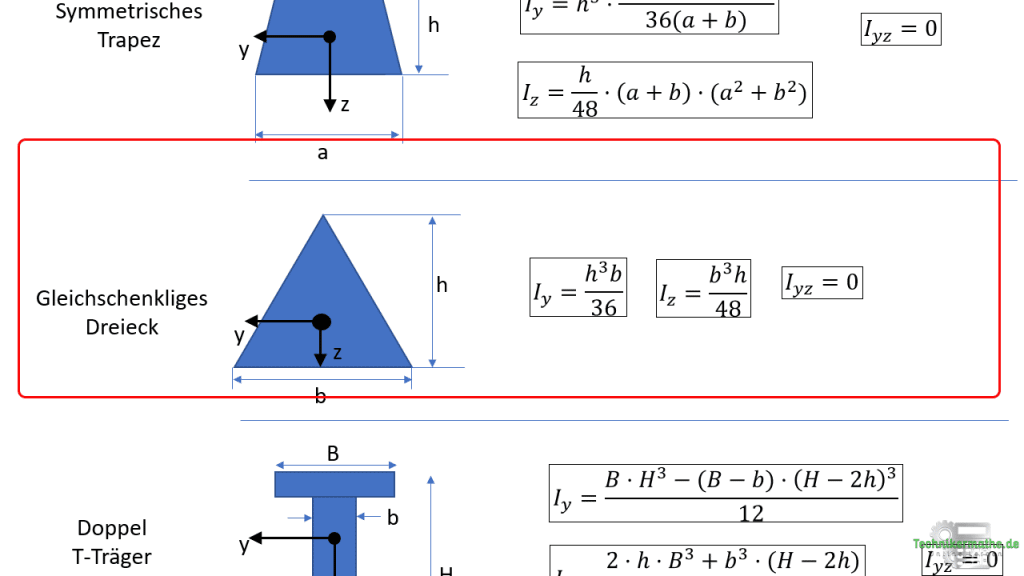
Aus der Tabelle (vorangegangene Lerneinheit dieser Lektion) kannst du die Gleichung zur Berechnung des Flächenträgheitsmoments für ein gleichschenkliges Dreieck entnehmen:

$I_y = \dfrac{h^3 \cdot b}{36}$

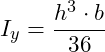
Einsetzen der gegebenen Abmessungen b = 2h und h = 0,4m:

$I_y = \dfrac{h^3 \cdot 2h}{36}$

$I_y = \dfrac{(0,4m)^3 \cdot 2 \cdot 0,4m}{36}$

$I_y = 0,0014m^4$

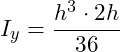
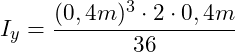
Schubspannungsverlauf

Nachdem nun alle Werte bestimmt sind, können wir den Schubspannungsverlauf für den Schnitt am Ende des Balkens berechnen:

Schubspannungsverlauf

$\tau(z) = \dfrac{Q \cdot S_y}{I_y \cdot b(z)}$

mit

$Q = 400 N$

$S_y = 0,0063m^3 - \dfrac{2}{3} \cdot z^3 - 0,2667m \cdot z^2$

$I_y = 0,0014m^4$

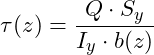
$b(z) =\dfrac{b}{h} \cdot z + \dfrac{2}{3} b$ mit b = 2h und h = 0,4m

Einsetzen der Werte:

$\tau(z) = \dfrac{400N \cdot (0,0063m^3 - \dfrac{2}{3} \cdot z^3 - 0,2667m \cdot z^2)}{0,0014m^4\cdot (2 \cdot z + \dfrac{2}{3} \cdot 0,8m)}$

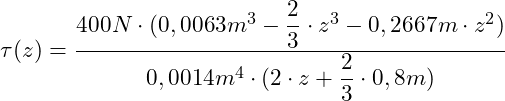
Zusammenfassen:

$\tau(z) = \dfrac{2,52Nm^3 - 266,67N \cdot z^3 - 106,68Nm \cdot z^2}{0,0028m^4 \cdot z + 0,0007m^5}$

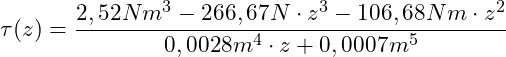
Hierbei handelt es sich um den Schubspannungsverlauf im Querschnitt am Balkenende (x = 5m) in Abhängigkeit von der z-Achse.

Maximale Schubspannung

Die maximale Schubspannung $\tau_{max}$ ist bei $z = 0$ gegeben, also im Schwerpunkt der Querschnittsfläche und damit im Koordinatenursprung des y,z-Koordinatensystems.

Wir setzen demnach z = 0 in die obige Gleichung ein, um die maximale Schubspannung zu erhalten:

$\tau(z) = \dfrac{2,52Nm^3 - 266,67N \cdot 0^3 - 106,68Nm \cdot 0^2}{0,0028m^4 \cdot 0 + 0,0007m^5}$

$\tau(z) = \dfrac{2,52Nm^3 }{ 0,0007m^5}$

$\tau(z) = 3.600 \frac{N}{m^2}$

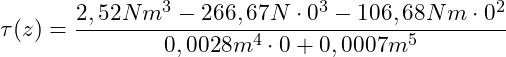
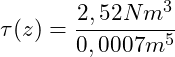
Die maximale Schubspannung beträgt am Ende des Balkens 3.600 N/m².

Was gibt es noch bei uns?

Optimaler Lernerfolg durch tausende Übungsaufgaben

Übungsbereich (Demo) - Lerne mit mehr als 4000 Übungsaufgaben für deine Prüfungen

Quizfrage 1

“Wusstest du, dass unter jedem Kursabschnitt eine Vielzahl von verschiedenen interaktiven Übungsaufgaben bereitsteht, mit denen du deinen aktuellen Wissensstand überprüfen kannst?”

Alle Technikerschulen im Überblick

Zum Verzeichnis der Technikerschulen (Alles Rund um die Schulen) — Zum Verzeichnis der Technikerschulen

Kennst du eigentlich schon unser großes Technikerschulen-Verzeichnis für alle Bundesländer mit allen wichtigen Informationen (Studiengänge, Kosten, Anschrift, Routenplaner, Social-Media) ? Nein? – Dann schau einfach mal hinein:

Was ist Technikermathe?

Unser Dozent Jan erklärt es dir in nur 2 Minuten!

Oder direkt den > kostenlosen Probekurs < durchstöbern? – Hier findest du Auszüge aus Alle Onlinekurse Technikermathe!

Geballtes Wissen in derzeit 26 Kursen

Hat dir dieses Thema gefallen? – Ja? – Dann schaue dir auch gleich die anderen Themen zu den Kursen

WT3 (Werkstoffprüfung) und
TM1 (Technische Mechanik – Statik) an.

Lerne nun erfolgreich mit unserem Onlinekurs Technische Mechanik 1 — TM1 (Technische Mechanik)

Lerne nun erfolgreich mit unserem Onlinekurs Werkstofftechnik 3 — WT3 (Werkstoffprüfung)

Perfekte Prüfungsvorbereitung für nur 14,90 EUR/Jahr pro Kurs

++ Günstiger geht’s nicht!! ++

Oder direkt Mitglied werden und Alle unsere Onlinekurse (inkl. Webinare + Unterlagen) sichern ab 7,40 EUR/Monat ++ Besser geht’s nicht!! ++