TM2 – Spannungstransformation – Ebener Spannungszustand [Erklärung, Formeln, Video, Beispiel]

Ein ebener Spannungszustand ist dann gegeben, wenn innerhalb eines dreidimensionalen Bauteils die Spannungen nur in in zwei Raumrichtungen auftreten.

Jetzt behandeln wir das Thema Ebener Spannungszustand und dazu dessen Koordinatentransformation zur Berechnung von Spannungen.

Für ein optimales Verständnis helfen dir zwei Videoclips und ein anschauliches Rechenbeispiel zu dem Thema.

Dieser Lerntext ist ein Auszug aus unserem Onlinekurs TM2 – Festigkeitslehre.

Ebener Spannungszustand – Einführung

Ein ebener Spannungszustand liegt zum Beispiel näherungsweise in Scheiben vor.

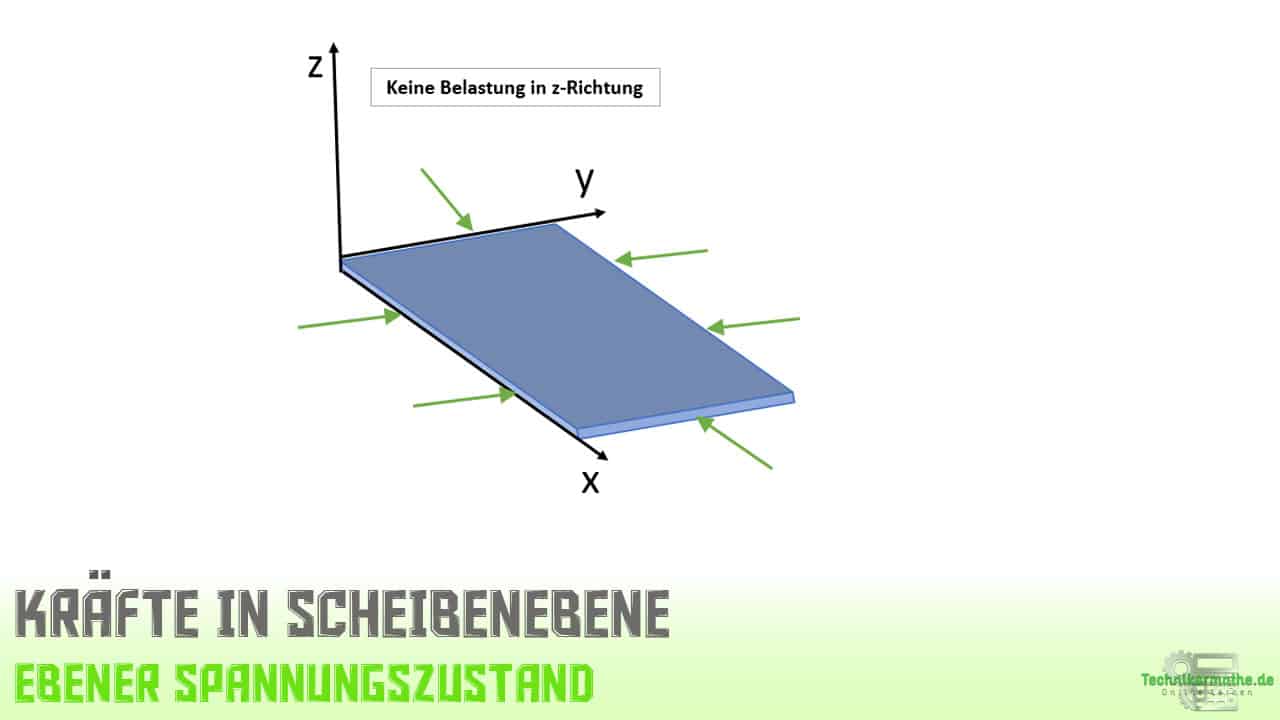
Scheibe, ebener Spannungszustand, Spannungen, Ebene — Ebener Spannungszustand – Scheibe

Eine Scheibe ist dadurch gekennzeichnet, dass ihre Dicke klein gegenüber den übrigen Abmessungen ist und dass sie nur in der x,y-Ebene belastet wird. Das bedeutet, dass die Spannungen, Verzerrungen und Verschiebungen nur von den x und y Koordinaten abhängen.

Dadurch, dass die Scheibe nur in der x,y-Ebene belastet wird, sind die Spannungen in der z-Richtung gleich Null:

$\sigma_z = 0$

$\tau_{xz} = \tau_{zx} = 0$

$\tau_{yz} = \tau_{zy} = 0$

Der Spannungstensor S reduziert sich im ebenen Spannungszustand auf 3 Spannungskomponenten:

Ebener Spannungstensor

$S = \begin{pmatrix} \sigma_x & \tau_{xy} \\ \tau_{yx} & \sigma_y \end{pmatrix}$

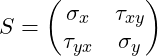
mit

$\tau_{xy} = \tau_{yx}$

Die Spannungen σ_x, σ_y und τ_xy sind diejenigen Spannungen, die in den Schnitten parallel zu den Koordinatenachsen auftreten. Schneiden wir also ein Stück so aus der Scheibe heraus, dass die Schnitte parallel zu den Koordinatenachsen sind, so erhalten wir die Spannungen wie folgt:

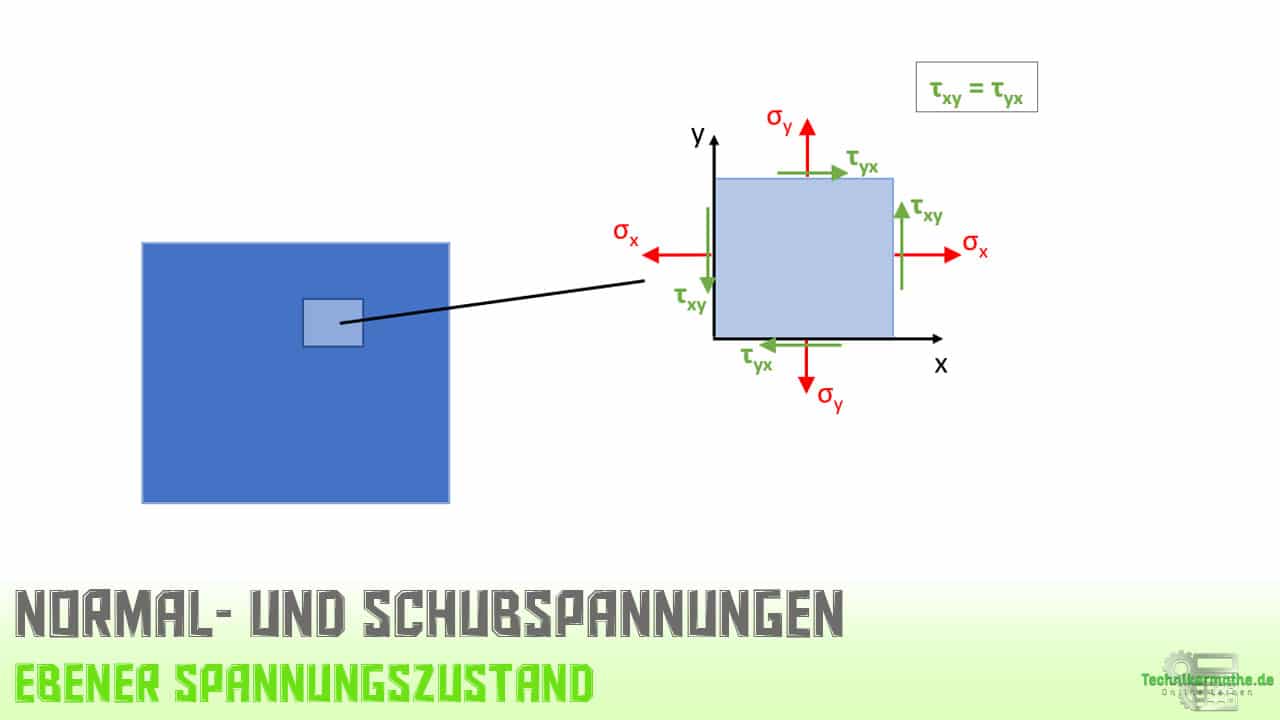
Spannungen, ebener Spannungszustand, Scheibe, Normalspannung, Schubspannung, Spannungstensor — Spannungen, ebener Spannungszustand

Wir gehen im Folgenden davon aus, dass die obigen Spannungen für Schnitte parallel zu den Koordinatenachsen bekannt sind. Wir können aus diesen gegebenen Spannungen dann auch diejenigen Spannungen berechnen, die nicht in Richtung der Koordinatenachsen zeigen, die also nicht in Schnitten auftreten, die parallel zu den Koordinatenachsen sind.

Video – Spannungstransformation

Im folgenden Videoclip zeigen wir dir, was genau die Spannungstransformation des ebenen Spannungszustand bedeutet und welche Formeln du hierfür benötigst.

Spannungstransformation – Formeln

Wir wollen uns jetzt anschauen, wie wir die Spannungen berechnen die bei einem Schnitt durch das Bauteil auftreten, welcher nicht parallel zu den Koordinatenachsen ist.

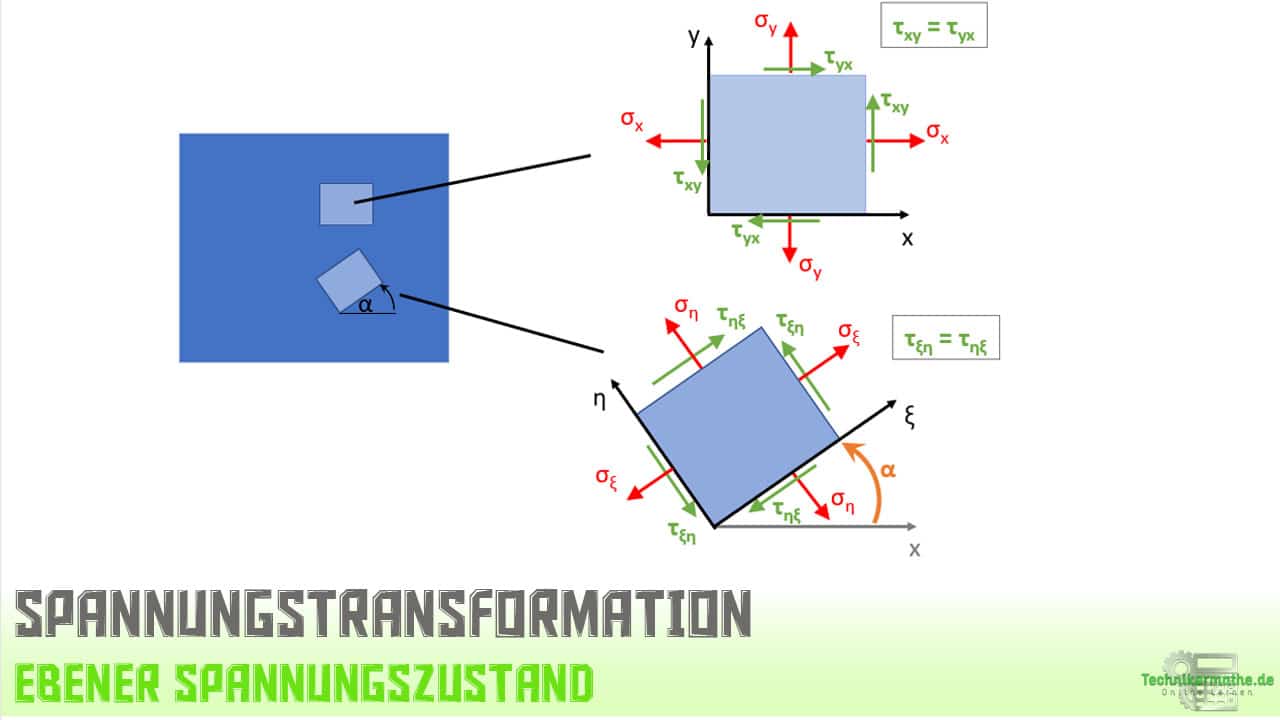
Spannungstransformation, ebener Spannungszustand, Koordinatentransformation, Formeln, Scheibe, Drehung des Koordinatensystems — Spannungstransformation, ebener Spannungszustand, Koordinatentransformation

In der obigen Grafik betrachten wir zum einen ein herausgeschnittenes ebenes Element, für welches die Schnitte parallel zu den x,y-Achsen liegen und zum anderen ein herausgeschnittenes Element, für welches die Schnitte nicht parallel zu den x,y-Achsen liegen.

Für das untere herausgeschnittene Element können wir neue Koordinatenachsen einführen und legen diese parallel zu den Schnittflächen. Die Beschriftung der Koordinatenachsen haben wir hier beliebig mit ξ (griechischer Buchstabe Xi) und η (griechischer Buchstabe Eta) gewählt.

Für das untere Element treten Normal- und Schubspannungen auf. Die Normalspannungen σ_ξ und σ_η stehen senkrecht auf den Schnittflächen, die Schubspannungen τ_ξη und τ_ηξliegen parallel zu den Schnittflächen.

Der Winkel α gibt die Drehung des Elements ausgehend von der x-Achse an.

Wir gehen davon aus, dass die Spannungen σ_x, σ_y sowie τ_xy für die Schnitte parallel zu den Koordinatenachsen bekannt sind.

Mit den gegebenen Spannungen σ_x, σ_yund τ_xy sowie dem Winkel α können wir die unbekannten Spannungen σ_ξ, σ_ηundτ_ξη berechnen. Dazu können wir die folgenden Formeln heranziehen:

$\sigma_{\xi} = \dfrac{\sigma_x + \sigma_y}{2} + \dfrac{\sigma_x - \sigma_y}{2} \cdot \cos(2 \alpha) + \tau_{xy} \cdot \sin(2 \alpha)$

$\sigma_{\eta} = \dfrac{\sigma_x + \sigma_y}{2} - \dfrac{\sigma_x - \sigma_y}{2} \cdot \cos(2 \alpha) - \tau_{xy} \cdot \sin(2 \alpha)$

$\tau_{\eta \xi} = \tau_{\xi \eta} = - \dfrac{\sigma_x - \sigma_y}{2} \cdot \sin(2 \alpha) + \tau_{xy} \cdot \cos(2 \alpha)$

Invarianten: Ebener Spannungszustand

Eine Invariante bezieht sich auf eine Eigenschaft oder Größe, die unter bestimmten Transformationen oder Operationen unverändert bleibt. Invariante Spannungen sind spezifische Spannungen in einem Material, die unter bestimmten Transformationen oder Belastungen unverändert bleiben.

Aus den obigen Transformationsbeziehungen kann man einfach beweisen, dass die Summe der Normalspannungen (1. Invariante) und die Determinante der Spannungsmatrix (2. Invariante) unabhängig von der Drehung des Koordinatensystems sind.

1.Invariante

Die 1. Invariante erhalten wir, indem wir die ersten beiden Transformationsgleichungen miteinander addieren ( $\sigma_{\xi} + \sigma_{\eta}$ ).

$I_1 = \sigma_x + \sigma_y = \sigma_{\xi} + \sigma_{\eta}$

Die Summe der Normalspannungen ist unabhängig von der Koordinatentransformation. Es handelt sich damit um eine Invariante.

2.Invariante

Die 2. Invariante erhalten wir, indem wir die Determinante der Spannungsmatrix für den ebenen Spannungszustand betrachten. Die Spannungsmatrix für den ebenen Spannungszustand ergibt sich wie folgt:

$S = \begin{pmatrix} \sigma_x & \tau_{xy} \\ \tau_{xy} & \sigma_y \end{pmatrix}$

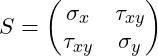
Die Determinante dieser Spannungsmatrix ergibt die 2. Invariante:

$I_2 = \sigma_x \cdot \sigma_y - \tau_{xy}^2 = \sigma_{\xi} \cdot \sigma_{\eta} - \tau_{\xi \eta}^2$

Die Determinante der Spannungsmatrix ist demnach invariant, d.h. unabhängig von der Drehung des Koordinatensystems.

Formeln richtig anwenden: Vorzeichen beachten

Für die obigen Formeln gilt die folgende Ausgangsituation für positive Spannungen:

Koordinatentransformation, ebener Spannungszustand, Spannungstransformation, positive Spannungen, Scheibe, Spannungen — Ausgangssituation für positive Spannungen

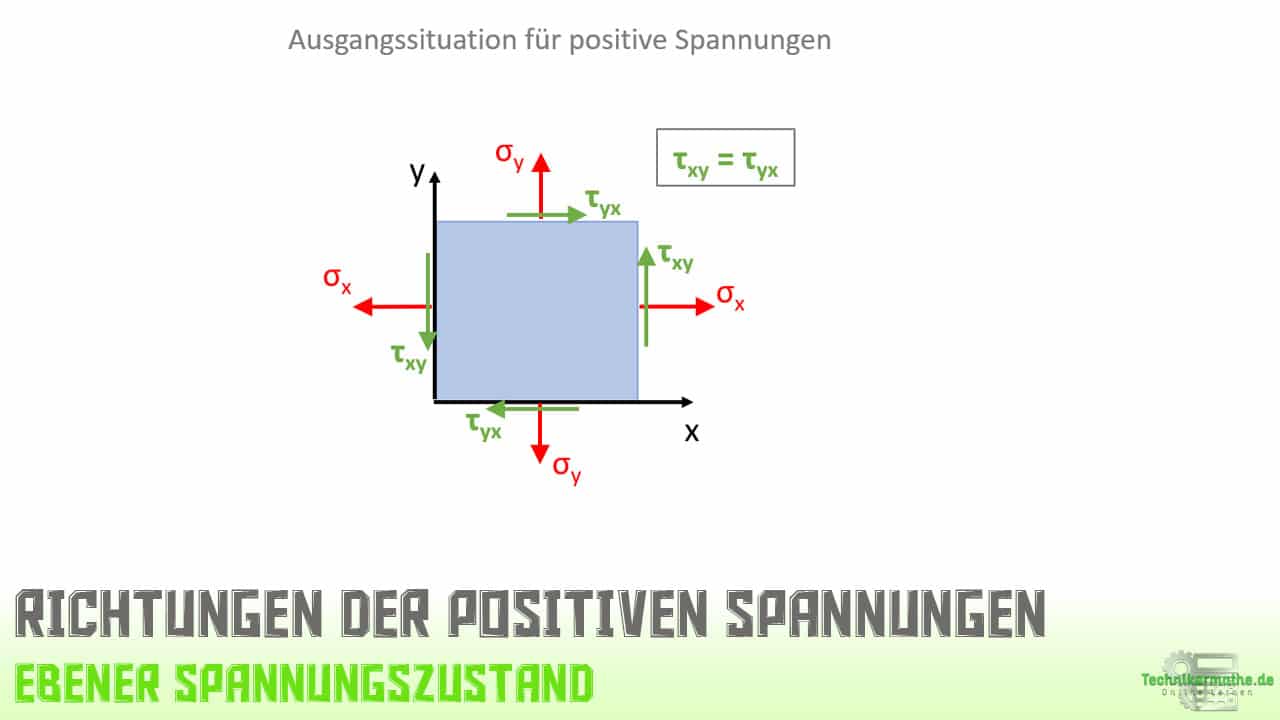
Sind positive Spannungen gegeben, so wirken diese in die oben gezeigten Richtungen. Bei negativen Spannungen wirken diese genau entgegengesetzt (um 180° gedreht). Die obigen Formeln gelten für positive Spannungen, sind also negative Spannungen gegeben, so müssen diese innerhalb der Formel mit einem Minuszeichen berücksichtigt werden.

Der Winkel α wird dann positiv berücksichtigt, wenn die Drehung des Ausgangskoordinatensystems in einer Linksdrehung (gegen den Uhrzeigersinn) erfolgt und negativ, wenn ein Rechtsdrehung (mit dem Uhrzeigesinn) des Ausgangskoordinatensystems stattfindet.

Schnittwinkel vs. Drehwinkel

Wenn wir aus einem ebenen Bauteil (z.B. einer Scheibe) ein Stück herausschneiden und die Spannungen abtragen, dann können wir entweder wie oben den Drehwinkel α im Bezug zum Ausgangskoordinatensystem angeben oder aber den Schnittwinkel β unter welchem der Schnitt durchgeführt wird:

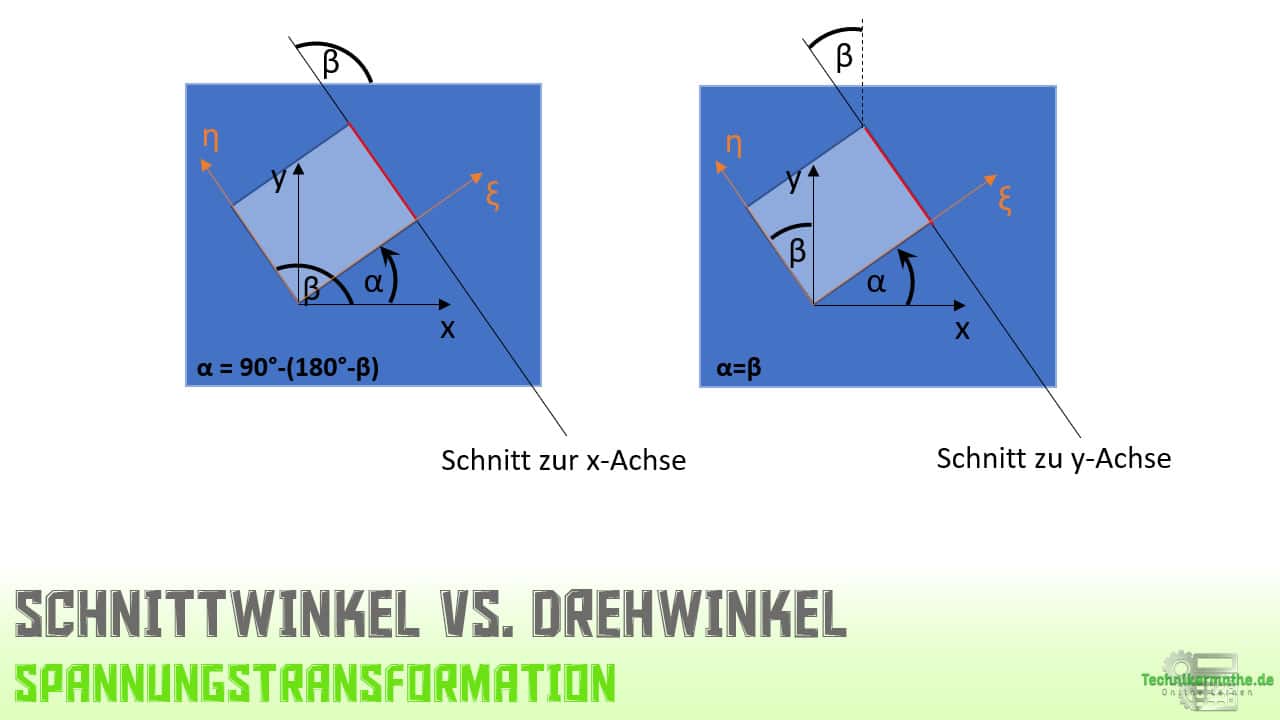
Spannungstransformation, ebener Spannungszustand, Schnittwinkel, Drehwinkel, Koordinatentransformation, Spannungen im ebenen Spannungszustand — Schnittwinkel vs. Drehwinkel – Spannungstransformation

In der obigen Grafik unterscheiden wir zwischen einem Schnittwinkel zur x-Achse und einem Schnittwinkel zur y-Achse. Je nachdem zu welcher Achse der Schnitt erfolgt, ergeben sich unterschiedliche Drehungen des Ausgangskoordinatensystems und damit unterschiedliche Drehwinkel.

Ist in der Aufgabe der Schnittwinkel β gegeben, so kannst du den Drehwinkel α, welchen du für die obigen Formeln benötigst, wie folgt berechnen:

Schnittwinkel zur x-Achse:

$\alpha = 90^\circ - (180^\circ - \beta)$

Schnittwinkel zur y-Achse:

$\alpha = \beta$

Video: Spannungstransformation – Beispiel

Im folgenden Videoclip zeigen wir dir ein Beispiel für die Berechnungen von Spannungen in einem gedrehten Koordinatensystem.

Prüfungsaufgabe 1: Spannungstransformation

Aufgabenstellung

Nun folgt eine Aufgabe zur Spannungstransformation – Gegeben sei eine Scheibe mit den folgenden Spannungswerten:

$\sigma_x = 80 Mpa$ ,

$\sigma_y = -50 MPa$ ,

$\tau_{xy} = -20 MPa$

Bestimme die Spannungen, wenn eine Drehung um 60° des Ausgangskoordinatensystems im Uhrzeigersinn erfolgt!

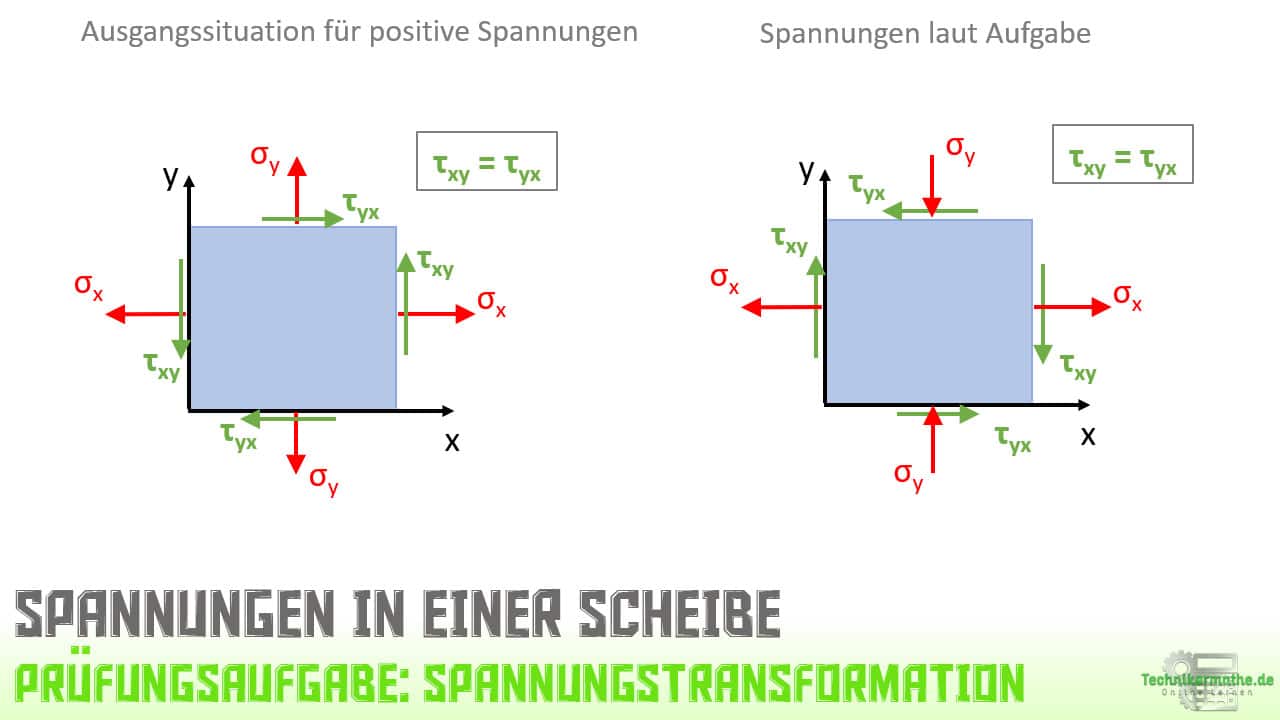
Aufgabe, Spannungstransformation, Ebener Spannungszustand, Scheibe, Spannungen — Beispiel: Spannungen in einer Scheibe

In der obigen Grafik siehst du links den Ausgangszustand für positive Spannungen. Sind hingegen negative Spannungen gegeben, so wirken die Spannungen genau entgegengesetzt. Die Normalspannung σ_y ist negativ und zeigt somit auf die Scheibe und auch die Schubspannung τ_xy bzw. τ_yx ist negativ und wirkt damit genau entgegengesetzt.

Wir wollen nun den Spannungszustand für eine Drehung des Ausgangskoordinatensystems um 60° im Uhrzeigersinn ermitteln. Hierbei handelt es sich um eine Rechtsdrehung, wir müssen den Winkel also negativ innerhalb der Formeln berücksichtigen.

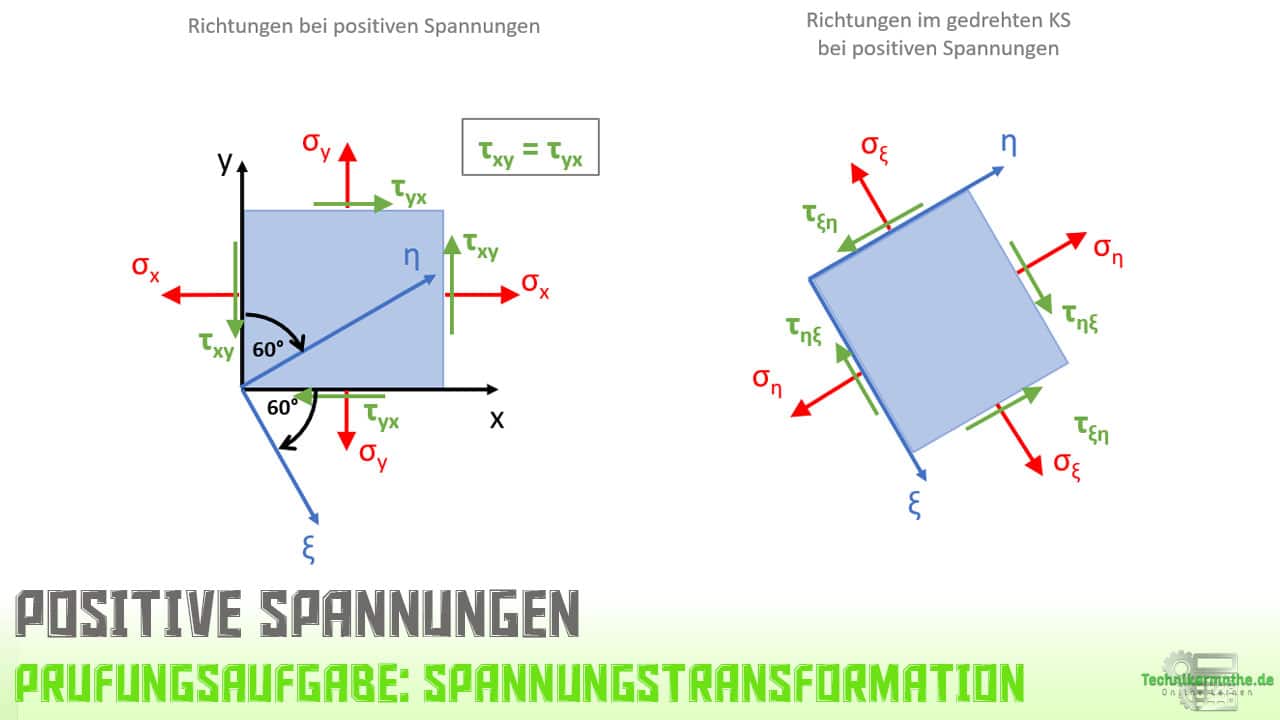
Koordinatentransformation, Spannungen, ebener Spannungszustand, Scheibe, Drehung des Koordinatensystems, Spannungstransformation — Spannungstransformation

In der obigen Grafik siehst du links die Ausgangssituation mit den Richtungen der Spannungen, wenn diese positiv gegeben sind. Drehst du nun dieses Koordinatensystem im Uhrzeigersinn um 60°, so ergeben sich die Spannungen wie rechts im Bild zu sehen ist. Die tatsächliche Richtung der Spannungen müssen wir aber noch berechnen. Resultierenden innerhalb der Berechnungen negative Werte, so müssen die Spannungen genau entgegengesetzt eingezeichnet werden.

Wir wenden die folgenden Formeln an, um die Aufgabe zu löse:

$\sigma_{\xi} = \dfrac{\sigma_x + \sigma_y}{2} + \dfrac{\sigma_x - \sigma_y}{2} \cdot \cos(2 \alpha) + \tau_{xy} \cdot \sin(2 \alpha)$

$\sigma_{\eta} = \dfrac{\sigma_x + \sigma_y}{2} - \dfrac{\sigma_x - \sigma_y}{2} \cdot \cos(2 \alpha) - \tau_{xy} \cdot \sin(2 \alpha)$

$\tau_{\eta \xi} = \tau_{\xi \eta} = - \dfrac{\sigma_x - \sigma_y}{2} \cdot \sin(2 \alpha) + \tau_{xy} \cdot \cos(2 \alpha)$

Wir setzen die folgenden Werte in die obigen Formeln ein:

$\sigma_x = 80 Mpa$

$\sigma_y = -50 MPa$

$\tau_{xy} = -20 MPa$

$\alpha = -60^\circ$

Und erhalten:

$\sigma_{\xi} = \dfrac{80 Mpa + (-50 MPa)}{2} + \dfrac{80 Mpa - (-50 MPa)}{2} \cdot \cos(2 (-60^\circ)) + (-20 MPa) \cdot \sin(2 (-60^\circ))= -0,18 MPa$

$\sigma_{\eta} = \dfrac{80 Mpa + (-50 MPa)}{2} - \dfrac{80 Mpa - (-50 MPa)}{2} \cdot \cos(2 (-60^\circ)) - (-20 MPa) \cdot \sin(2 (-60^\circ))= 30,18 MPa$

$\tau_{\eta \xi} = \tau_{\xi \eta} = - \dfrac{80 Mpa - (-50 MPa)}{2} \cdot \sin(2 \alpha) + (-20 MPa) \cdot \cos(2 (-60^\circ))= 66,29 MPa$

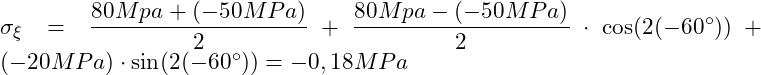
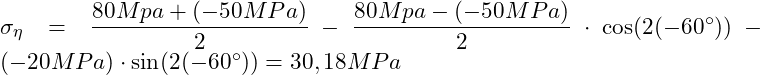
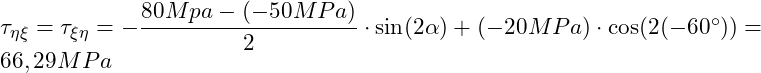
Wir haben nun die Spannungen bestimmt. Diese wirken wie folgt:

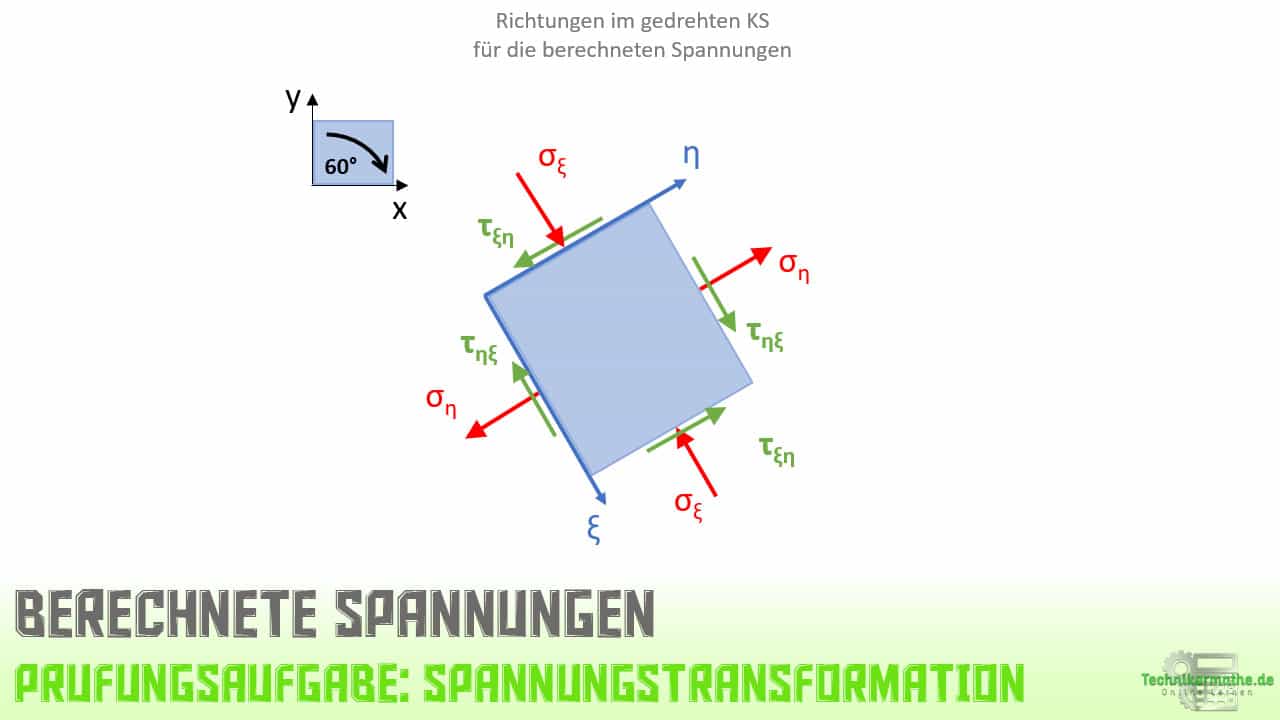
Ebener Spannungszustand, Spannungstransformation, Koordinatentransformation, Spannungen, Scheibe, Drehung des Koordinatensystems — Koordinatentransformation

Die Normalspannung σ_ξ ist negativ und wirkt demnach genau entgegengesetzt.

wie gehts weiter?

Nachdem du jetzt weisst, was ein ebener Spannungszustand ist und wie mit diesem Berechnungen durchgeführt werden, schauen wir uns in der folgenden Lerneinheit eine Prüfungsaufgabe an, in welcher du die Anwendung der obigen Formeln erlernst. Danach wird das Thema Ebener Spannungszustand dir keine Probleme mehr bereiten.

Was gibt es noch bei uns?

Optimaler Lernerfolg durch tausende Übungsaufgaben

Quizfrage 1

“Wusstest du, dass unter jedem Kursabschnitt eine Vielzahl von verschiedenen interaktiven Übungsaufgaben bereitsteht, mit denen du deinen aktuellen Wissensstand überprüfen kannst?”

Alle Technikerschulen im Überblick

Zum Verzeichnis der Technikerschulen (Alles Rund um die Schulen) — Zum Verzeichnis der Technikerschulen

Kennst du eigentlich schon unser großes Technikerschulen-Verzeichnis für alle Bundesländer mit allen wichtigen Informationen (Studiengänge, Kosten, Anschrift, Routenplaner, Social-Media) ? Nein? – Dann schau einfach mal hinein:

Was ist Technikermathe?

Unser Dozent Jan erklärt es dir in nur 2 Minuten!

Oder direkt den > kostenlosen Probekurs < durchstöbern? – Hier findest du Auszüge aus Alle Onlinekurse Technikermathe!

Geballtes Wissen in derzeit 26 Kursen

Hat dir dieses Thema gefallen? – Ja? – Dann schaue dir auch gleich die anderen Themen zu den Kursen

WT3 (Werkstoffprüfung) und
TM1 (Technische Mechanik – Statik) an.

Lerne nun erfolgreich mit unserem Onlinekurs Technische Mechanik 1 — TM1 (Technische Mechanik)

Lerne nun erfolgreich mit unserem Onlinekurs Werkstofftechnik 3 — WT3 (Werkstoffprüfung)

Perfekte Prüfungsvorbereitung für nur 14,90 EUR/Jahr pro Kurs

++ Günstiger geht’s nicht!! ++

Oder direkt Mitglied werden und Alle unsere Onlinekurse (inkl. Webinare + Unterlagen) sichern ab 7,40 EUR/Monat ++ Besser geht’s nicht!! ++