TM2 – Prüfungsaufgabe: Normalspannung & Verschiebung im Stab [Formel, Beispiel, Video]

In dieser Lerneinheit schauen wir uns eine Aufgabe an, in welcher wir die Normalspannung, die Verschiebung und die Längenänderung eines hängenden Stabs bestimmen wollen.

Für ein optimales Verständnis helfen dir drei ausführliche Videoclips und zwei anschauliche Rechenbeispiele zu dem Thema.

Dieser Lerntext ist ein Auszug aus unserem Onlinekurs TM2 – Festigkeitslehre.

Ganz unten auf der Seite findest du die die gleiche Aufgabe mit unterschiedlichen Werten als Video.

Prüfungsaufgabe: Hängender Stab – Normalspannung und Verschiebung

Aufgabenstellung

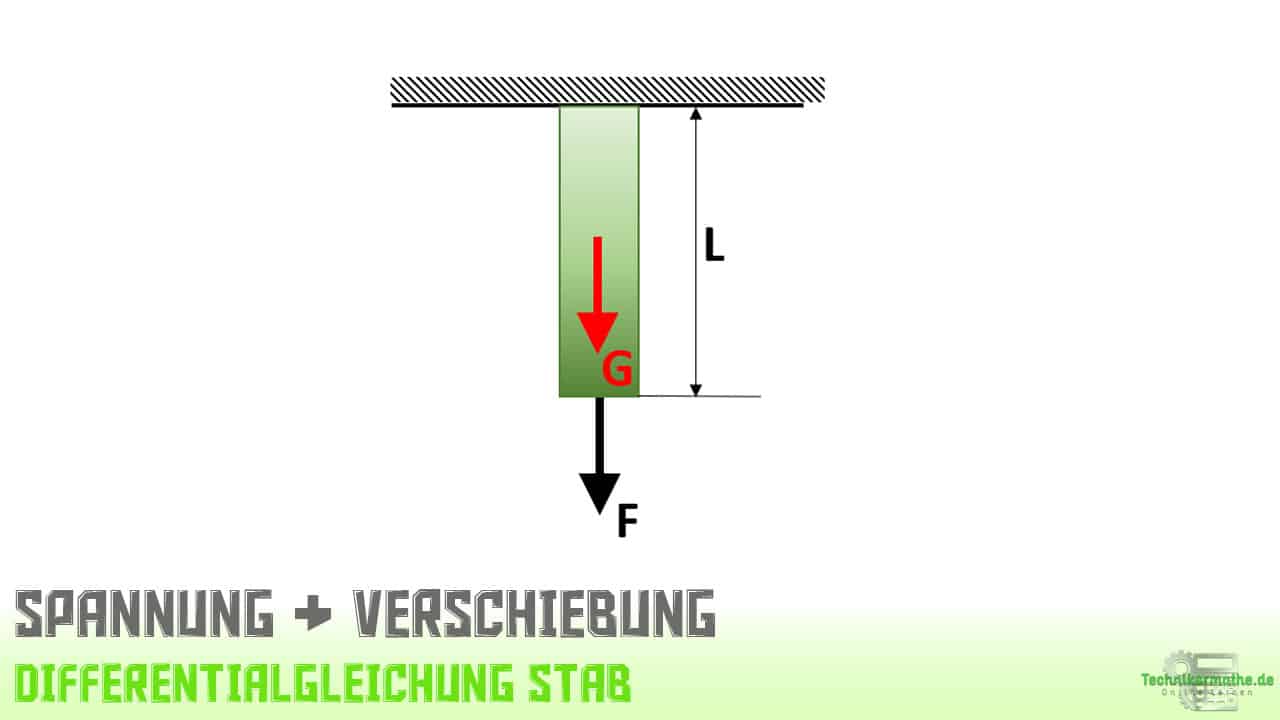
Hängender Stab, Normalspannung, Verschiebung, Beispiel, Stabverlängerung, Längenänderung — Hängender Stab: Normalspannung, Verschiebung, Stabverlängerung

Gegeben sei ein Stab der Länge L = 50 cm und einer Querschnittsfläche von A = 25cm², welcher am oberen Ende fest eingespannt ist. Der Stab weist eine Gewichtskraft von G = 20 N auf und wird durch eine Zugkraft am unteren Ende von F = 15 N belastet. Der Elastizitätsmodul beträgt E = 2,1 · 10¹¹ N/m².

a) Bestimme die Normalspannung in Abhängigkeit von x!

b) Bestimme die Verschiebung in Abhängigkeit von x!

c) Bestimme die Stabverlängerung!

Lösung a) Normalspannung berechnen

Wir wollen zunächst die Normalspannung in Abhängigkeit von x bestimmen. Diese können wir bestimmen zu:

$\sigma = \dfrac{N}{A}}$

Wir müssen also zunächst die Normalkraft bestimmen. Dazu führen wir einen Schnitt durch den Stab durch und tragen die Normalkraft N ab:

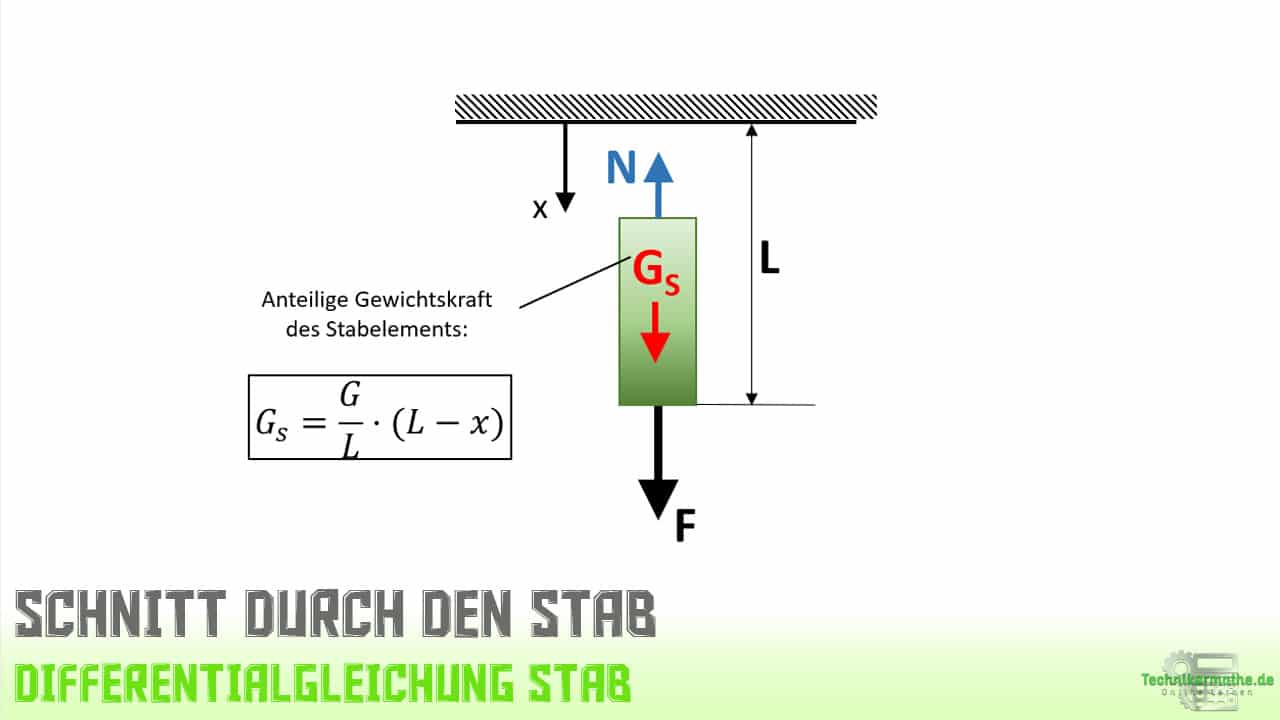
Hängender Stab, Normalspannung, Verschiebung, Normalkraft, Schnitt, Zugkraft — Normalkraft im hängenden Zugstab

Der Schnitt wird in Abhängigkeit von x durchgeführt. Wir betrachten zur Berechnung der Normalkraft N das untere Stabelement. Dieses Stabelement weist nicht die volle Gewichtskraft G auf. Je größer wir den Schnitt von der Einspannung entfernt vornehmen, desto kleiner wird das Stabelement und desto weniger Gewicht weist dieses auf.

Die anteilige Gewichtskraft (wir bezeichnen sie einfach mit G_S) können wir mittels Dreisatz berechnen:

G → L (Gewichtskraft gilt bei Länge L)

Wir haben eine Länge des Stabelements von L – x gegeben. Bei dieser Länge ergibt sich die gesuchte anteilige Gewichtskraft:

GS → L-x

Wir wenden nun den Dreisatz an und erhalten:

$G_s = \dfrac{G}{L} \cdot (L-x)$

Wir können als nächstes die Normalkraft N aus der vertikalen Gleichgewichtsbedingung berechnen:

$\sum F_{iy} = 0$ Die Summe aller vertikalen Kräfte muss Null ergeben

Wir wählen als Vorzeichenkonvention, dass alle nach oben gerichteten Kräfte positiv berücksichtigt werden:

$N - G_s - F = 0$

Wir haben alle vertikalen Kräfte am Stabelement berücksichtigt. Wir lösen die Gleichung als nächstes nach der gesuchten Normalkraft N auf:

$N = G_s + F$

$N = \dfrac{G}{L} \cdot (L-x) +F$

Einsetzen der gegebenen Werte:

$N = \dfrac{20 N}{0,5m} \cdot (0,5m-x) +15 N$

Auflösen der Klammer:

$N(x) = -40 \frac{N}{m} x + 35 N$ Normalkraftverlauf

Die gegebene Normalkraft ist abhängig von x, also davon wo genau der Schnitt durchgeführt wird. Wird zum Beispiel der Schnitt direkt an der Einspannung durchgeführt, dann ist x = 0 und die Normalspannung beträgt:

$N(x = 0) = -40 \frac{N}{m} \cdot 0 + 35 N = 35N$

Die Normalspannung beträgt dort 35N, weil die gesamte Gewichtskraft sowie die Zugkraft wirken.

Wir der Schnitt bei L = 25cm (bei der Hälfte des Stabs) durchgeführt, so beträgt die Normalkraft:

$N(x = 0,25m) = -40 \frac{N}{m} \cdot 0,25m + 35 N = 25N$

In diesem Fall geht nur die Hälfte der Gewichtskraft in die Berechnung ein.

Bei x = 50 cm wirkt nur noch die Zugkraft F:

$N(x = 0,5m) = -40 \frac{N}{m} \cdot 0,5m + 35 N = 15N$

Wir suchen die Normalspannung und können dazu die folgende Gleichung heranziehen:

$\sigma = \dfrac{N}{A}$

Einsetzen des Normalkraftverlaufs sowie der Querschnittsfläche:

$\sigma(x) = \dfrac{-40 \frac{N}{m} x + 35 N}{0,0025m^2}$

$\sigma(x) = -16.000 \frac{N}{m^3} x + 14.000 \frac{N}{m^2}$ Normalspannungsverlauf

Dadurch, dass der Normalkraftverlauf abhängig von x ist, ist auch die Normalspannung σ abhängig von x.

Bei der Einspannung bei x = 0 ist eine Normalspannung von σ = 14.000 N/m² gegeben bzw. 1,4 N/cm² und am Stabende bei x = L = 50 cm ergibt sich eine Normalspannung von σ = 6.000 N/m² bzw. 0,6 N/cm².

Lösung b) Verschiebung bestimmen

Wir können zur Bestimmung der Verschiebung in Abhängigkeit von x (also vom Schnitt) die Differentialgleichung der Verschiebung heranziehen:

$EAu'' = -n$

$EAu' = N(x)$

Da wir den Normalkraftverlauf bereits bestimmt haben, können wir die zweite Gleichung heranziehen:

$EAu' = -40 \frac{N}{m} x + 35 N$

Wir können diese Gleichung nun einmal integrieren:

$EAu = \int (-40 \frac{N}{m} x + 35 N) dx$

$EAu = (-40 \frac{N}{m} \frac{1}{2} x^2 + 35 N \cdot x + C)$

$EAu = - 20 \frac{N}{m} x^2 + 35 N \cdot x + C$

Was kommt als Nächstes?

Wichtig: Hier muss eine Integrationskonstante berücksichtigt werden, die wir als nächstes aus den Randbedingungen berechnen können.

Integrationskonstante aus Randbedingungen

Die Randbedingungen sind an den Stabenden gegeben, also bei x = 0 und bei x = L. Wir müssen uns nun überlegen, welche Randbedingung eine Aussage zur Verschiebung u zulässt. Da bei x = 0 der Stab fest eingespannt ist, kann sich dieses Ende nicht verschieben. Es gilt also: u = 0. Bei x = 0 gilt also u = 0. Diesen Zusammenhang setzen wir in die obige Gleichung ein:

$EA \cdot 0 = -20 \frac{N}{m} 0^2 + 35 N \cdot 0 + C$

$\rightarrow: \; C = 0$

Damit ergibt sich also:

$EAu = -20 \frac{N}{m} x^2 + 35 N \cdot x$

Auflösen nach der Verschiebung:

$u = \dfrac{-20 \frac{N}{m} x^2 + 35 N \cdot x}{EA}$

Einsetzen von A = 0,0025m² und E = 2,1 · 10¹¹ N/m²:

$u = \dfrac{-20 \frac{N}{m} x^2 + 35 N \cdot x}{525 \cdot 10^6 \frac{N}{m^2}}$ Verschiebung in Abhängigkeit von x

Wir können nun die Verschiebung im Stab für einzelne Schnitte berechnen, indem wir für x die Werte einsetzen, für welche wir die Verschiebung im Stab bestimmen wollen.

Lösung c) Stabverlängerung berechnen

Die Stabverlängerung können wir nun berechnen, indem wir ganz einfach die Differenz der Verschiebungen an den Stabenden bestimmen:

$\triangle l = u(L) - u(0) = 0,00001cm - 0cm = 0,00001 cm$

Der Stab verlängert sich um 0,00001 cm infolge der Gewichtskraft G und der Zugkraft F.

Video: Hängender Stab

In den folgenden beiden Videos zeigen wir dir, wie du die Normalspannung sowie den Verschiebungsverlauf für einen hängenden Zugstab berechnen kannst.

Was gibt es noch bei uns?

Optimaler Lernerfolg durch tausende Übungsaufgaben

Übungsbereich (Demo) - Lerne mit mehr als 4000 Übungsaufgaben für deine Prüfungen

Quizfrage 1

“Wusstest du, dass unter jedem Kursabschnitt eine Vielzahl von verschiedenen interaktiven Übungsaufgaben bereitsteht, mit denen du deinen aktuellen Wissensstand überprüfen kannst?”

Alle Technikerschulen im Überblick

Zum Verzeichnis der Technikerschulen (Alles Rund um die Schulen) — Zum Verzeichnis der Technikerschulen

Kennst du eigentlich schon unser großes Technikerschulen-Verzeichnis für alle Bundesländer mit allen wichtigen Informationen (Studiengänge, Kosten, Anschrift, Routenplaner, Social-Media) ? Nein? – Dann schau einfach mal hinein:

Was ist Technikermathe?

Unser Dozent Jan erklärt es dir in nur 2 Minuten!

Oder direkt den > kostenlosen Probekurs < durchstöbern? – Hier findest du Auszüge aus Alle Onlinekurse Technikermathe!

Geballtes Wissen in derzeit 26 Kursen

Hat dir dieses Thema gefallen? – Ja? – Dann schaue dir auch gleich die anderen Themen zu den Kursen

WT3 (Werkstoffprüfung) und
TM1 (Technische Mechanik – Statik) an.

Lerne nun erfolgreich mit unserem Onlinekurs Technische Mechanik 1 — TM1 (Technische Mechanik)

Lerne nun erfolgreich mit unserem Onlinekurs Werkstofftechnik 3 — WT3 (Werkstoffprüfung)

Perfekte Prüfungsvorbereitung für nur 14,90 EUR/Jahr pro Kurs

++ Günstiger geht’s nicht!! ++

Oder direkt Mitglied werden und Alle unsere Onlinekurse (inkl. Webinare + Unterlagen) sichern ab 7,40 EUR/Monat ++ Besser geht’s nicht!! ++