TM2 – Prüfungsaufgabe: Normalspannung im konischen Stab [Formel, Berechnung]

In dieser Lerneinheit betrachten wir eine Aufgabe zur Berechnung der Normalspannung in einem Stab mit veränderlichem Querschnitt.

Jetzt schauen wir uns die Berechnung der Normalspannung mit Hilfe einer Prüfungsaufgabe an.

Für ein optimales Verständnis helfen dir drei ausführliche Videoclips und zwei anschauliche Rechenbeispiele zu dem Thema.

Dieser Lerntext ist ein Auszug aus unserem Onlinekurs TM2 – Festigkeitslehre.

Prüfungsaufgabe: Normalspannung berechnen (konischer Stab)

Aufgabenstellung

Normalspannung, Stab, veränderlicher Querschnitt, konischer Stab, Beispiel, Spannungen im Stab, Zugstab, kegelförmiger Stab — Prüfungsaufgabe: Normalspannung berechnen (konischer Stab)

In der obigen Grafik siehst du einen konisch verlaufenden Stab mit runder Querschnittsfläche, welcher auf Zug mit der Kraft F = 60 N belastet wird. Die Länge des Stabes betrage L = 1,2m. Der Radius am Anfang des Stabes sei gegeben mit r₀ = 0,2m.

a) Bestimme die Normalspannung bei einem senkrechten Schnitt bei beliebigem Querschnitt (ohne Zahlenwerte)!

b) Berechne die Normalspannung bei einem senkrechten Schnitt bei x = 1m!

Normalspannungsverlauf bestimmen

Wir sollen einen senkrechten Schnitt durch den obigen Stab durchführen. Da der Stab konisch (=kegelförmig, veränderlicher Querschnitt) verläuft, also im Querschnitt nicht konstant ist, ist die auftretende Normalspannung abhängig davon, wo genau der Schnitt durchgeführt wird. Somit ist die Normalspannung in jedem Schnittbereich unterschiedlich.

Die Normalspannung im Stab bei einem senkrechten Schnitt können wir wie folgt berechnen:

$\sigma_0 = \dfrac{N}{A}$

Da nun sich aber die Querschnittsfläche A mit zunehmendem x ändert, ändert sich auch die Normalspannung $\sigma_0$ . Je größer die Querschnittsfläche A wird, desto kleiner wird die Normalspannung $\sigma$ .

Wir haben einen Stab mit runder Querschnittsfläche gegeben. Die Fläche eines Kreises wird mit der folgenden Formel berechnet:

$A = \pi \cdot r^2$

Da der Radius sich ändert (er wird mit zunehmendem x größer), müssen wir hier zunächst die Funktion des Radius berechnen:

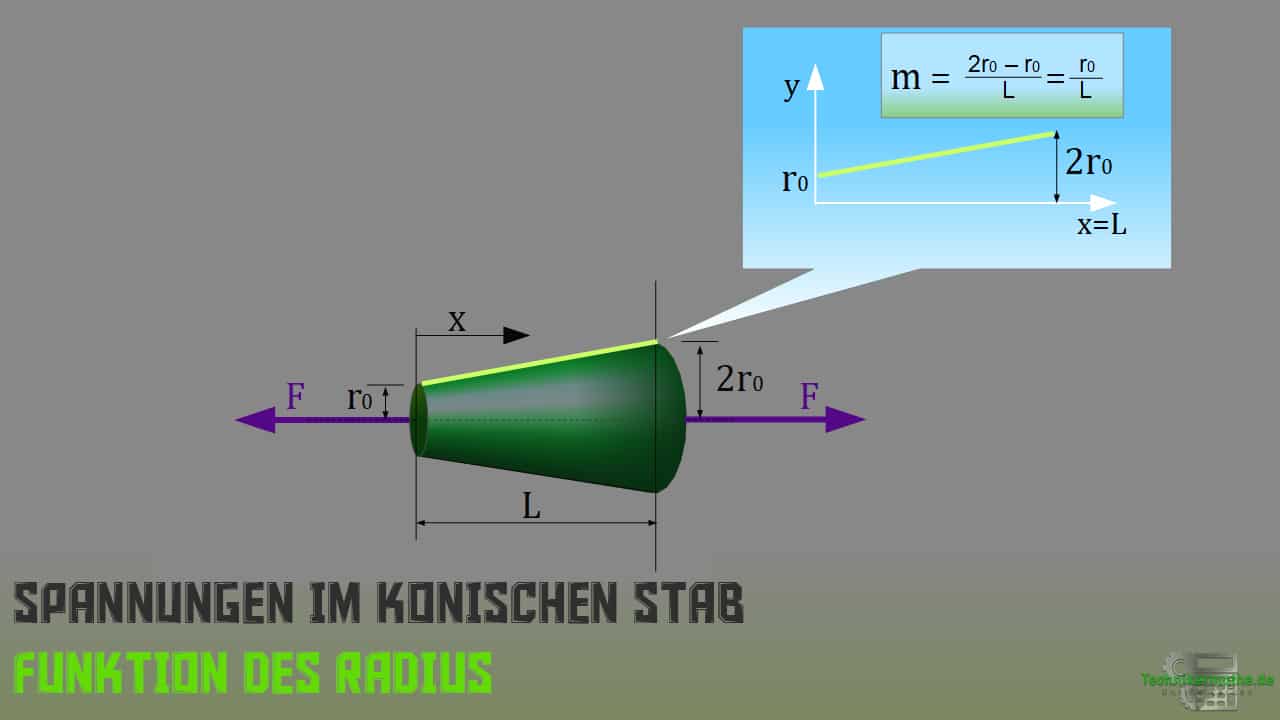
Normalspannung berechnen, konischer Stab, Normalspannung, Stab, veränderlicher Querschnitt, lineare Funktionsgleichung, lineare Funktion, Steigung, kegelförmiger Stab — Steigung bestimmen, konischer Stab

In der obigen Grafik siehst du in grün die Funktion des Radius ausgehend von der Stabachse. Dieser beginnt bei r₀ und endet bei 2r₀. Wir können diese Funktion (in grün) in ein x,y-Koordinatensystem übertragen und hier die lineare Funktionsgleichung anwenden:

$y = m \cdot x + b$

Der y-Wert ist nichts anderes als der Radius r(x):

$r(x) = m \cdot x + b$

Wir können nun die Steigung m berechnen, indem wir vom Stabanfang ausgehend L Schritte nach rechts gehen (in positive x-Richtung) und dann 2r₀ – r₀ = r₀ Schritte nach oben (in positive y-Richtung).

Damit erhalten wir:

$m = \dfrac{\text{Schritte in y-Richtung}}{\text{Schritte in x-Richtung}}$

$m = \dfrac{r_0}{L}$

Wir setzen die Steigung m ein:

$r(x) = \dfrac{r_0}{L} \cdot x + b$

Der Schnittpunkt mit der y-Achse ist gegeben bei b = r₀:

$r(x) = \dfrac{r_0}{L} \cdot x + r_0$ Funktion des Radius

Führen wir nun zum Beispiel einen senkrechten Schnitt bei x = 1m durch, so erhalten wir den Radius der Querschnittsfläche an dieser Stelle.

Fläche berechnen

Wir können nun mit der obigen Funktion für den Radius die Querschnittsfläche in Abhängigkeit von x bestimmen.

$A = \pi \cdot r^2$

$A = \pi \cdot (\dfrac{r_0}{L} \cdot x + r_0)^2$

Normalspannung berechnen

Die Normalspannung berechnen wir bei einem senkrechten Schnitt mit der folgenden Gleichung:

$\sigma_0 = \dfrac{N}{A}$

Zunächst setzen wir die Fläche ein:

$\sigma_0 = \dfrac{N}{\pi \cdot (\dfrac{r_0}{L} \cdot x + r_0)^2}$

Wir benötigen noch die Größe der Normalkraft. Wir haben zwar schon in den vorangegangenen Abschnitten die Normalkraft für einen Zugstab bestimmt, wollen hier aber trotzdem nochmal aufführen, wie wir diese aus der horizontalen Gleichgewichtsbedingung berechnen.

Dazu führen wir einen senkrechten Schnitt durch den Stab und tragen die auftretende Normalkraft ab:

Normalspannung, konischer Stab, kegelförmiger Stab, Schnitt, Normalkraft, senkechter Schnitt — Normalkraft: Konischer Stab

Gleichgewichtsbedingung in x-Richtung:

$\sum F_{ix} = 0}$

$-F + N = 0$

$N = F$

Einsetzen in die Gleichung:

$\sigma_0 = \dfrac{F}{\pi \cdot (\dfrac{r_0}{L} \cdot x + r_0)^2}$ Normalspannungsverlauf (konischer Stab)

Wir haben nun den Normalspannungsverlauf für den obigen Stab in Abhängigkeit vom Schnitt bestimmt.

Normalspannung berechnen

Wir haben nun alle relevanten Größen berechnet und können nun die Zahlenwerte einsetzen.

r₀ = 0,2m | L = 1,2m | F = 60 N | x = 1m

$\sigma_0 = \dfrac{60 N}{\pi \cdot (\dfrac{0,2m}{1,2m} \cdot 1m + 0,2m)^2} = 142,06 frac{N}{m^2}$

Die Normalspannung bei einem senkrechten Schnitt bei x = 1m beträgt für den obigen konischen Stab 142,06 N/m².

Was gibt es noch bei uns?

Optimaler Lernerfolg durch tausende Übungsaufgaben

Übungsbereich (Demo) - Lerne mit mehr als 4000 Übungsaufgaben für deine Prüfungen

Quizfrage 1

“Wusstest du, dass unter jedem Kursabschnitt eine Vielzahl von verschiedenen interaktiven Übungsaufgaben bereitsteht, mit denen du deinen aktuellen Wissensstand überprüfen kannst?”

Alle Technikerschulen im Überblick

Zum Verzeichnis der Technikerschulen (Alles Rund um die Schulen) — Zum Verzeichnis der Technikerschulen

Kennst du eigentlich schon unser großes Technikerschulen-Verzeichnis für alle Bundesländer mit allen wichtigen Informationen (Studiengänge, Kosten, Anschrift, Routenplaner, Social-Media) ? Nein? – Dann schau einfach mal hinein:

Was ist Technikermathe?

Unser Dozent Jan erklärt es dir in nur 2 Minuten!

Oder direkt den > kostenlosen Probekurs < durchstöbern? – Hier findest du Auszüge aus Alle Onlinekurse Technikermathe!

Geballtes Wissen in derzeit 26 Kursen

Hat dir dieses Thema gefallen? – Ja? – Dann schaue dir auch gleich die anderen Themen zu den Kursen

WT3 (Werkstoffprüfung) und
TM1 (Technische Mechanik – Statik) an.

Lerne nun erfolgreich mit unserem Onlinekurs Technische Mechanik 1 — TM1 (Technische Mechanik)

Lerne nun erfolgreich mit unserem Onlinekurs Werkstofftechnik 3 — WT3 (Werkstoffprüfung)

Perfekte Prüfungsvorbereitung für nur 14,90 EUR/Jahr pro Kurs

++ Günstiger geht’s nicht!! ++

Oder direkt Mitglied werden und Alle unsere Onlinekurse (inkl. Webinare + Unterlagen) sichern ab 7,40 EUR/Monat ++ Besser geht’s nicht!! ++