TM2 – Normalspannung bei reiner Biegung [Definition, Formel, Beispiel]

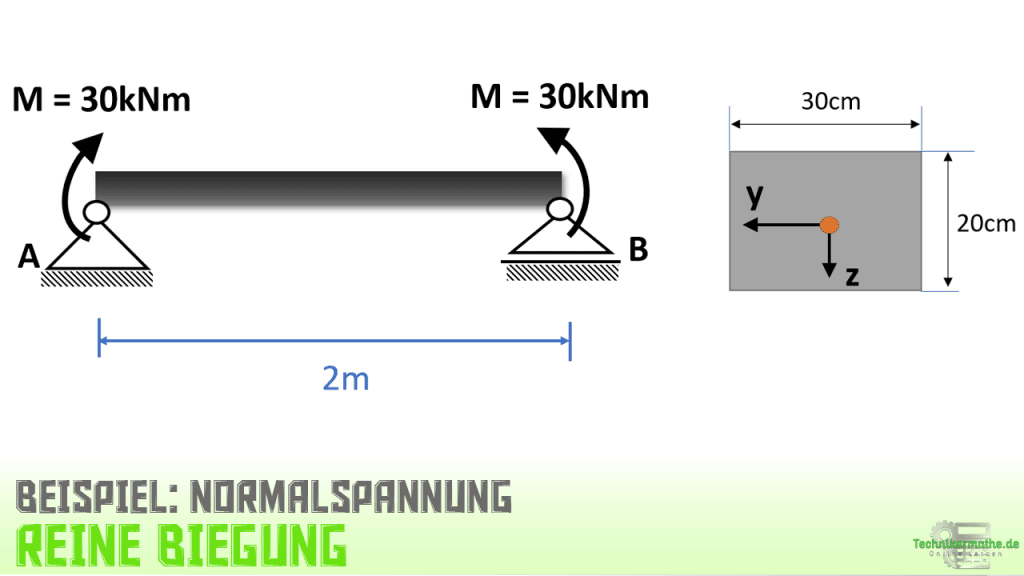
In dieser Lerneinheit betrachten wir die reine Biegung am Balken. Reine Biegung ist dann gegeben, wenn jeweils ein Moment an den Balkenenden angebracht wird. Bei reiner Biegung ist der Querkraftverlauf Null und der Momentenverlauf konstant.

In dieser Lerneinheit wollen wir uns mit Hilfe einer typischen Klausuraufgabe anschauen, wie die Normalspannung bei reiner Biegung berechnet wird.

Dieser Lerntext ist ein Auszug aus unserem Onlinekurs TM2 – Festigkeitslehre.

Reine Biegung – Definition

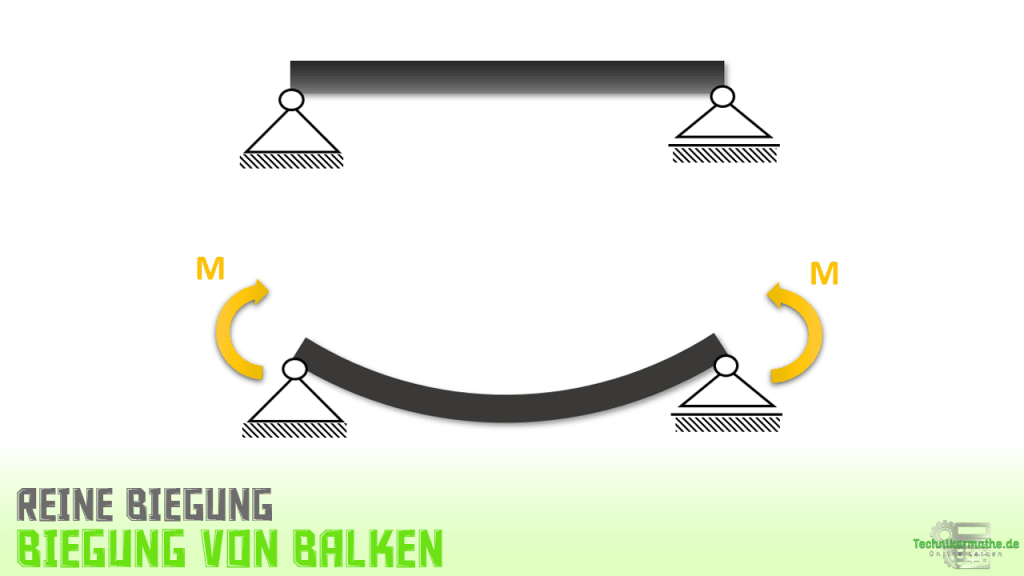
Reine Biegung, querkraftfreie Biegung, Biegung, Normalspannung bei reiner Biegung, Normalspannung, Durchbiegung, Momentenverlauf — Reine Biegung

Eine reine Biegung bzw. querkraftfreie Biegung entsteht durch das Aufbringen zweier Momente an den Ende eines Balkens. Das Schnittmoment ist in diesem Fall im gesamten Balken konstant.

Normalspannung – Formel

Bei einer reinen Biegung treten Normalspannungen aber keine Schubspannungen auf. Die Berechnung der Normalspannungen erfolgt über die folgende Gleichung (auf die Herleitung sei verzichtet):

Normalspannung

$\sigma_x = \dfrac{M}{I_{y}} \cdot z$

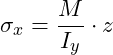
Hierbei ist

$M$ = Schnittmoment (Schnittgröße M bestimmen)

$I_y$ = Flächenträgheitsmoment in Bezug auf die y-Achse (Betrachtung des Querschnitts)

$z$ = Abstand zur neutralen Faser in z-Richtung (Betrachtung des Querschnitts)

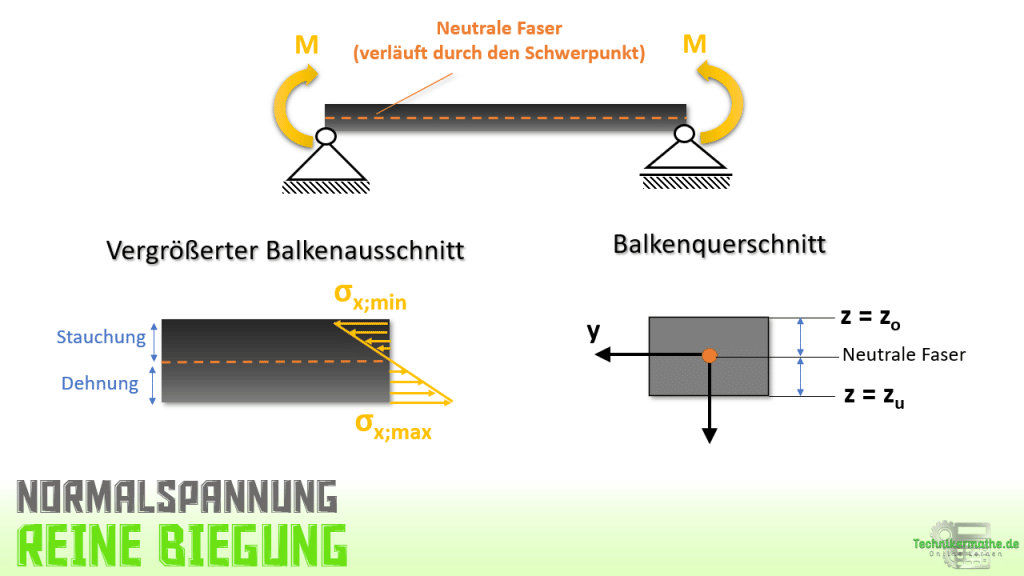
Normalspannung bei reiner Biegung, reine Biegung, Normalspannung, Biegung, Neutrale Faser, Moment — Normalspannungen bei reiner Biegung

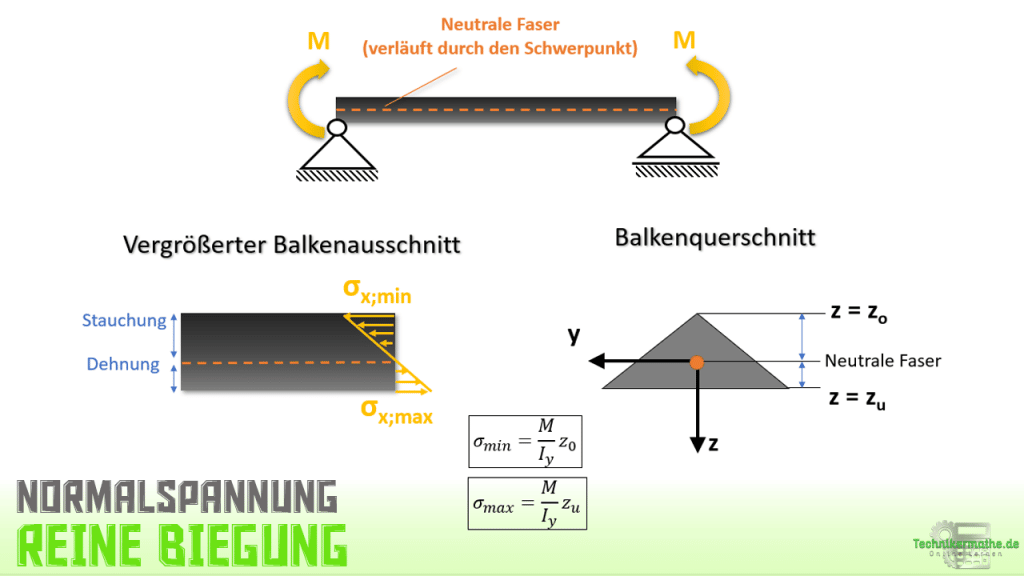
Der Balken in der obigen Grafik wird infolge der auftretenden Momente an den Balkenenden nach unten gebogen. Betrachten wir den vergrößerten Balkenausschnitt, so tritt oberhalb der neutralen Faser eine Stauchung und unterhalb der neutralen Faser eine Dehnung des Balkens auf. Damit ergeben sich oberhalb der neutralen Faser Druckspannungen (=negative Normalspannungen) und unterhalb der neutralen Faser Zugspannungen (=positive Normalspannungen). Die Normalspannung an der neutralen Faser ist gleich Null.

Maximale Normalspannung

Merk’s dir!

Das Spannungsmaximum bzw. Spannungsminimum findet sich infolge der angenommenen linearen Verteilung der Spannung dort, wo der Abstand zur neutralen Faser am Größten ist (an den Randfasern).

Im obigen Fall (rechteckiger Querschnitt) liegt der Schwerpunkt genau in der Mitte und damit auch die neutrale Faser. Die Abstände zur oberen Randfaser z₀ und zur unteren Randfaser z_u sind demnach identisch. Somit sind minimale und maximale Normalspannungen betragsmäßig gleich groß.

$\sigma_{x;min} = \dfrac{M}{I_{y}} \cdot z_o$

$\sigma_{x;max} = \dfrac{M}{I_{y}} \cdot z_u$

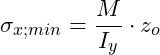
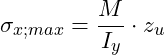
In der nachfolgenden Grafik siehst du einen dreieckigen Querschnitt. Hier sind die Abstände zu den Randfasern (ausgehend von der neutralen Faser) nicht mehr identisch. Der Abstand z₀ ist größer als z_u. Damit ist die minimale Normalspannung betragsmäßig größer als die maximale Normalspannung:

Normalspannung bei reiner Biegung, Randfaser, Neutrale Faser, Spannung — Normalspannungen bei reiner Biegung, Randfaser, Neutrale Faser, Spannung

Prüfungsaufgabe : Normalspannungen bei reiner Biegung

Aufgabenstellung

Beispiel, reine Biegung, querkraftfreie Biegung, Spannung, Normalspannung, Biegespannung — Beispiel: Normalspannung (reine Biegung)

Gegeben sei der obige Balken, der durch zwei Momente an den Balkenenden belastet wird. Bestimme die auftretende maximale und minimale Normalspannungen!

Wir haben hier reine Biegung gegeben, da nur äußere Momente an den Balkenenden angreifen. Damit liegt im gesamten Balken ein konstantes Biegemoment vor.

Die Gleichung zur Berechnung der Normalspannungen lautet:

$\sigma_x = \dfrac{M}{I_{y}} \cdot z$

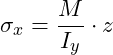
Wir suchen das Spannungsminimum und Spannungsmaximum, die an den Randfasern auftritt:

$\sigma_{x;min} = \dfrac{M}{I_{y}} \cdot z_0$

$\sigma_{x;max} = \dfrac{M}{I_{y}} \cdot z_u$

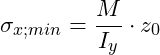
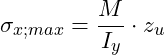
Biegemoment berechnen

Zunächst berechnen wir das Biegemoment, welches im gesamten Balken konstant ist. Wir können also irgendwo einen gedanklichen Schnitt durch den Balken durchführen, das Biegemoment abtragen und dann aus der Momentengleichgewichtsbedingung berechnen.

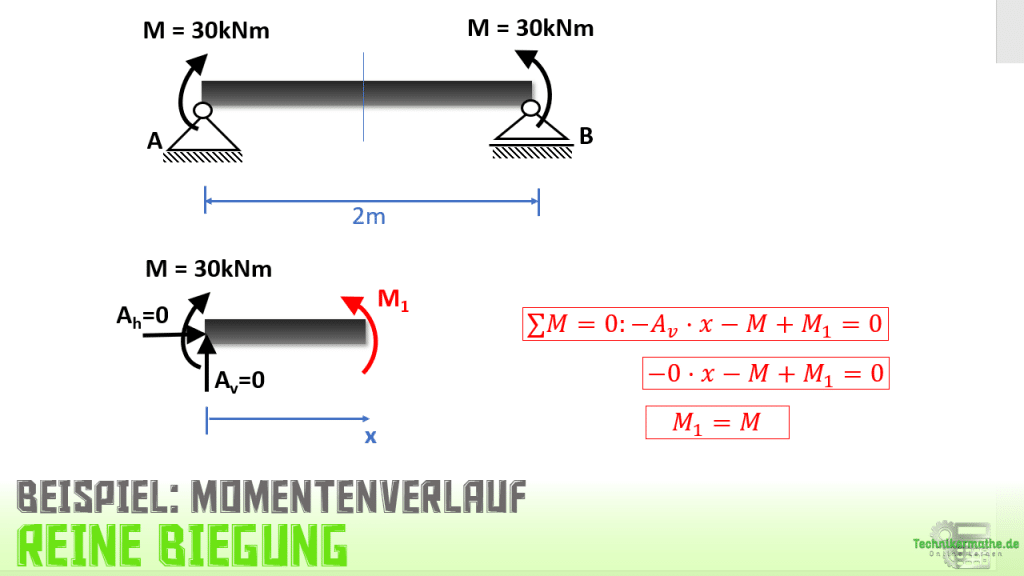
Reine Biegung, Momentenverlauf, Beispiel, Biegemoment, Schnittgrößen, Beispiel — Momentenverlauf bei reiner Biegung

Zuvor müssen natürlich die Lagerkräfte berechnet werden. Da wir aber keine äußeren Querkräfte (vertikalen Kräfte) und keine äußeren Normalkräfte (Horizontalkräfte) gegeben haben, werden die Auflagerkräfte A_h und A_v zu Null.

Wir können als nächstes die Momentengleichgewichtsbedingung zur Berechnung des Schnittmoments M₁ aufstellen:

$\sum M = 0$ :

$-A_v \cdot x - M + M_1 = 0$

Auflösen nach M₁:

$M_1 = A_v \cdot x + M$

Mit A_v = 0 ergibt sich:

$M_1 = M$

$M_1 = 30 kNm$

Bei reiner Biegung im gesamten Balken ist das Schnittmoment gleich dem angreifenden äußeren Moment.

Merk’s dir!

Die Berechnung von Schnittgrößen findest du detailliert in unserem Kurs TM1-Statik.

Flächenträgheitsmoment berechnen

Im nächsten Schritt berechnen wir das Flächenträgheitsmoment bezüglich der y-Achse. Dazu betrachten wir den Balkenquerschnitt. Es handelt sich hierbei um eine rechteckige Fläche. Wir können das Flächenträgheitsmoment aus Tabellenwerken entnehmen bzw. aus der Lerneinheit Flächenträgheitsmomente einiger Querschnitte):

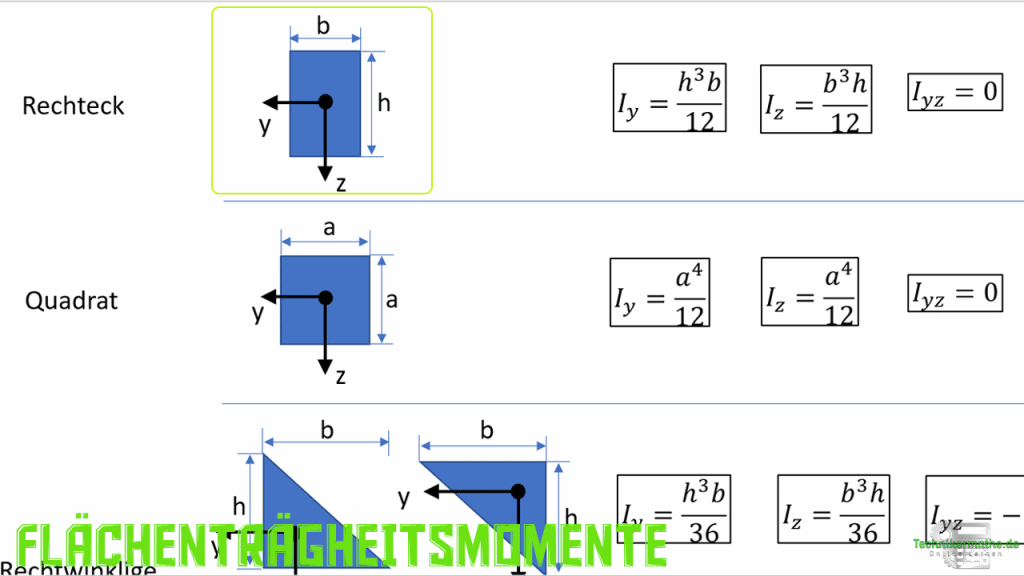
Reine Biegung, Beispiel, Normalspannung, Flächenträgheitsmoment, Rechteck — Flächenträgheitsmomente: Rechteck

Wir übernehmen die Gleichungen und setzen die Werte aus der Aufgabenstellung ein:

$I_y = \dfrac{h^3 \cdot b}{12} = \dfrac{(20cm)^3 \cdot 30cm}{12} = 20.000cm^4$

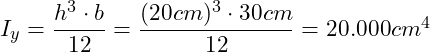
Abstände zur Randfaser

Als letztes benötigen wir noch die Abstände von der neutralen Faser hin zu den Randfasern, also zur oberen und unteren Randfaser. Dazu betrachten wir auch wieder den Querschnitt. Die Randfaser verläuft durch den Schwerpunkt, welcher sind bei einem Rechteck genau in der Mitte befindet:

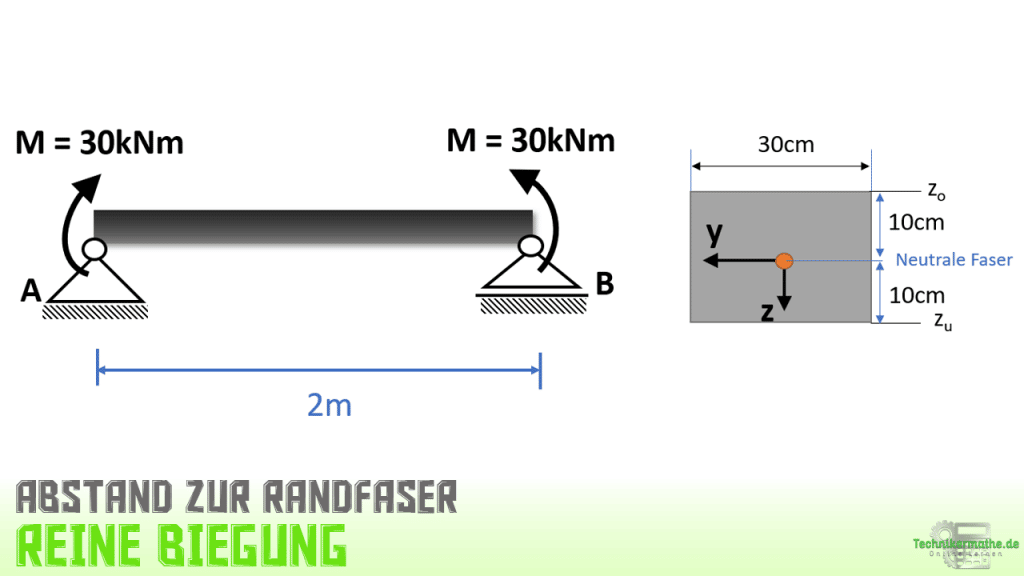
Reine Biegung, Normalspannung, Randfaser, Momentenverlauf, Abstand, Balken, Moment, Querschnitt — Abstand zur Randfaser – Reine Biegung

Die Abstände zur oberen Randfaser z₀ und zur unteren Randfaser z_u ausgehend von der neutralen Faser sind für ein Rechteck betragsmäßig gleich groß:

$z_o = -10cm$ (negative z-Achse)

$z_u = 10 cm$

Normalspannung berechnen

Im letzten Schritt können wir die Normalspannung berechnen:

$\sigma_{x;min} = \dfrac{M}{I_y} \cdot z_0$

$\sigma_{x;max} = \dfrac{M}{I_y} \cdot z_u$

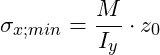
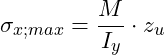
Wir haben das Biegemoment in kNm gegeben, die Flächenträgheitsmomente in cm⁴ und die Abstände zur Randfaser in cm. Wir haben hier nun zwei Maßeinheiten für die Länge gegeben, einmal Meter [m] und einmal Zentimeter [cm]. Wir müssen uns hier für eine Längeneinheit entscheiden und wählen Zentimeter. So müssen wir zunächst das Moment in kNcm umrechnen:

$1m = 100 cm$

$3 kNm = 3 kN \cdot 100 cm = 300 kNcm$

Einsetzen ergibt:

$\sigma_{x;min} = \dfrac{300 kNcm}{20.000cm^4} \cdot (-10cm) = -0,15 \frac{kN}{cm^2}$

$\sigma_{x;max} = \dfrac{300 kNcm}{20.000cm^4} \cdot 10cm = 0,15 \frac{kN}{cm^2}$ $

Die minimale bzw. maximale Normalspannung beträgt an den Randfaser 0,15 kN/cm².

Was kommt als Nächstes?

In der folgenden Lerneinheit betrachten wir die Querkraftbiegung und die Berechnung der damit auftretenden Normalspannung und Schubspannung.

Was gibt es noch bei uns?

Optimaler Lernerfolg durch tausende Übungsaufgaben

Quizfrage 1

“Wusstest du, dass unter jedem Kursabschnitt eine Vielzahl von verschiedenen interaktiven Übungsaufgaben bereitsteht, mit denen du deinen aktuellen Wissensstand überprüfen kannst?”

Alle Technikerschulen im Überblick

Zum Verzeichnis der Technikerschulen (Alles Rund um die Schulen) — Zum Verzeichnis der Technikerschulen

Kennst du eigentlich schon unser großes Technikerschulen-Verzeichnis für alle Bundesländer mit allen wichtigen Informationen (Studiengänge, Kosten, Anschrift, Routenplaner, Social-Media) ? Nein? – Dann schau einfach mal hinein:

Was ist Technikermathe?

Unser Dozent Jan erklärt es dir in nur 2 Minuten!

Oder direkt den > kostenlosen Probekurs < durchstöbern? – Hier findest du Auszüge aus Alle Onlinekurse Technikermathe!

Geballtes Wissen in derzeit 26 Kursen

Hat dir dieses Thema gefallen? – Ja? – Dann schaue dir auch gleich die anderen Themen zu den Kursen

WT3 (Werkstoffprüfung) und
TM1 (Technische Mechanik – Statik) an.

Lerne nun erfolgreich mit unserem Onlinekurs Technische Mechanik 1 — TM1 (Technische Mechanik)

Lerne nun erfolgreich mit unserem Onlinekurs Werkstofftechnik 3 — WT3 (Werkstoffprüfung)

Perfekte Prüfungsvorbereitung für nur 14,90 EUR/Jahr pro Kurs

++ Günstiger geht’s nicht!! ++

Oder direkt Mitglied werden und Alle unsere Onlinekurse (inkl. Webinare + Unterlagen) sichern ab 7,40 EUR/Monat ++ Besser geht’s nicht!! ++