TM2 – Hauptnormalspannung berechnen [Erklärung, Video, Berechnung]

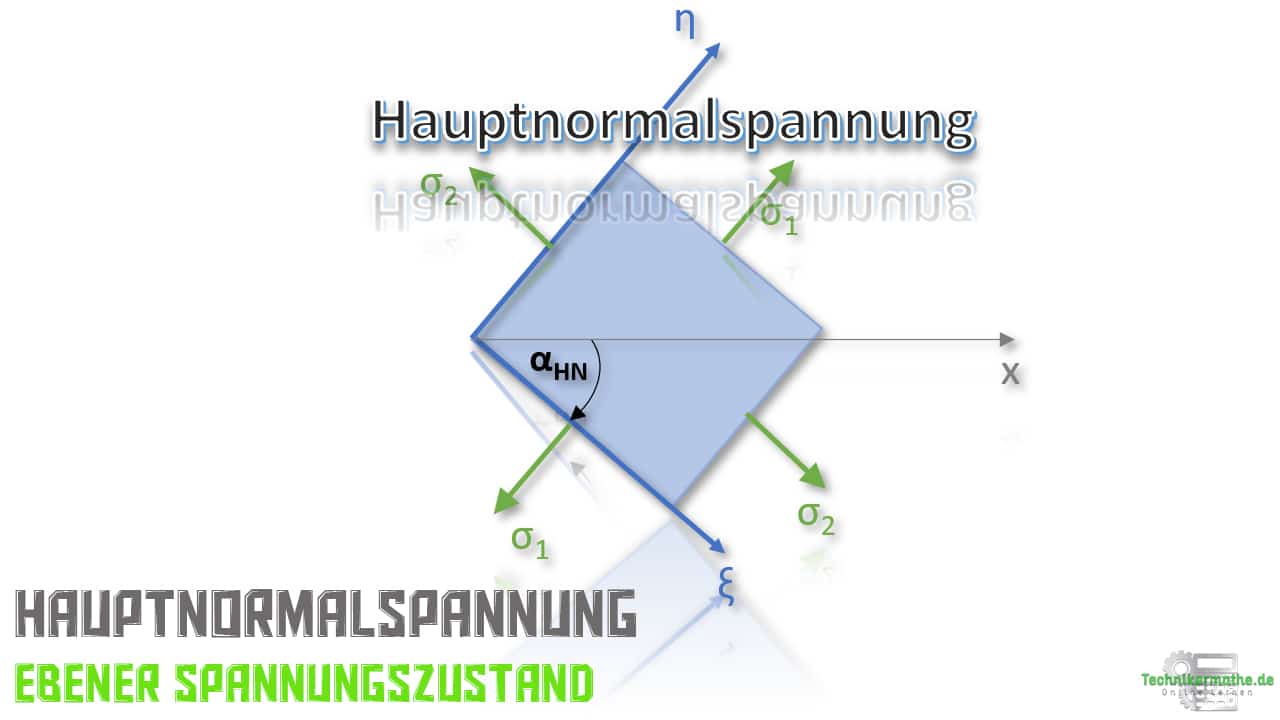
Hauptspannungen sind die Extremwerte der Spannungen und unterteilen sich in die Hauptnormalspannungen und Hauptschubspannungen. Die Hauptnormalspannungen sind die Extremwerte der Normalspannungen, die Hauptschubspannungen die Extremwerte der Schubspannungen.

Wir wollen in dieser Lerneinheit die Hauptnormalspannungen berechnen.

Für ein optimales Verständnis helfen dir drei ausführliche Videoclips und zwei anschauliche Rechenbeispiele zu dem Thema.

Dieser Lerntext ist ein Auszug aus unserem Onlinekurs TM2 – Festigkeitslehre.

Wichtig bei der Dimensionierung von Bauteilen und bei der Auswahl von Materialien sind die maximalen Spannungswerte, die nicht überschritten werden dürfen. Deswegen ist es von besonderem Interesse diese maximal auftretenden Spannungen innerhalb eines ebenen Bauteils zu kennen. Diese maximalen Werte werden auch als Hauptspannungen bezeichnet.

Uns interessiert in diesem Zusammenhang welchen Wert die Hauptspannungen annehmen können und unter welchem Winkel diese auftreten.

Die Extremwerte der Spannungen werden auch als Hauptspannungen bezeichnet und unterteilen sich in die Hauptnormalspannungen und Hauptschubspannungen. Die Hauptnormalspannungen sind die Extremwerte der Normalspannungen, die Hauptschubspannungen die Extremwerte der Schubspannungen.

Wir betrachten zunächst die Hauptnormalspannungen.

Hauptnormalspannung & Hauptrichtung

Die Hauptnormalspannungen kannst du mit den folgenden beiden Gleichung bestimmen:

$\sigma_{1} = \dfrac{\sigma_x + \sigma_y}{2} + \sqrt{\dfrac{\sigma_x - \sigma_y}{2})^2 + \tau_{xy}^2}$

$\sigma_{2} = \dfrac{\sigma_x + \sigma_y}{2} - \sqrt{\dfrac{\sigma_x - \sigma_y}{2})^2 + \tau_{xy}^2}$

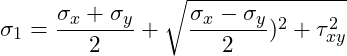
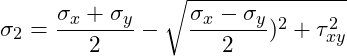
Die Hauptnormalspannung kann die beiden Extremwerte σ₁ und σ₂ annehmen.

Merk’s dir!

Beim Auftreten der Hauptnormalspannungen fallen die Schubspannungen weg. In diesem Fall gilt also $\tau_{xy} = 0$ .

Die Hauptrichtung α_HN ist der Winkel der Koordinatendrehung unter welchem die Hauptnormalspannungen auftreten. Du kannst diesen Winkel mittels der folgenden Gleichung berechnen:

$\tan(2 \alpha_{HN}) = \dfrac{2 \cdot \tau_{xy}}{\sigma_x - \sigma_y}$

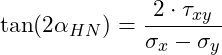
Die Hauptrichtung wird in den meisten Fällen wie oben angegeben. Um nun den Winkel aus dieser Gleichung bestimmen zu können, müssen wir diese noch umstellen. Dazu wenden wir den Arkustangens (tan^-1) auf beiden Seiten an:

$2 \alpha_{HN} = \tan^{-1}(\dfrac{2 \cdot \tau_{xy}}{\sigma_x - \sigma_y})$

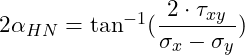
Danach teilen wir beide Seiten durch 2 und erhalten:

$\alpha_{HN} = \frac{1}{2} \cdot \tan^{-1}(\dfrac{2 \cdot \tau_{xy}}{\sigma_x - \sigma_y})$

Merk’s dir!

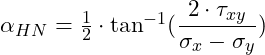
Bei der Hauptrichtung α_HNhandelt es sich um den Winkel der Koordinatendrehung, also um die Drehung der x-Achse.

Um herauszufinden, welche der beiden Hauptnormalspannungen σ₁ und σ₂ dann in Richtung der gedrehten x-Achse (der ξ-Achse) zeigt, kannst du den Winkel ganz einfach die Transformationsgleichungen des ebenen Spannungszustands einsetzen:

$\sigma_{\xi} = \dfrac{\sigma_x + \sigma_y}{2} + \dfrac{\sigma_x - \sigma_y}{2} \cdot \cos(2 \alpha) + \tau_{xy} \cdot \sin(2 \alpha)$

Video: Hauptnormalspannungen berechnen

Im folgenden Video zeige ich dir, wie du die Hauptnormalspannungen berechnest.

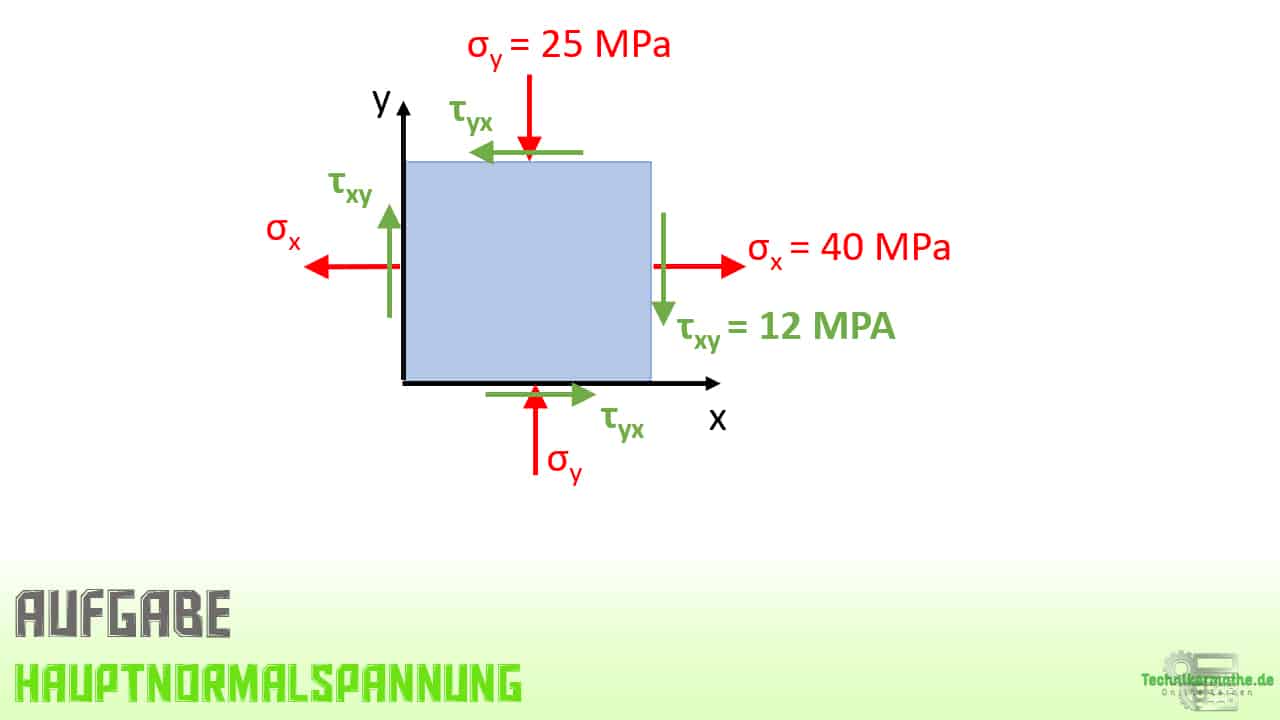
Aufgabe: Hauptnormalspannung berechnen

Aufgabenstellung

Gegeben sei der folgende Spannungszustand:

Hauptnormalspannung berechnen, ebener Spannungszustand, Beispiel, Hauptnormalspannungen, Normalspannungen, Koordinatentransformation, Spannungstransformation — Beispiel: Hauptnormalspannungen berechnen

Gegeben sei der obige ebene Spannungszustand. Berechne die Hauptnormalspannungen und den Winkel, unter welchem diese auftreten.

Zur Berechnung der Hauptnormalspannungen benötigen wir die folgenden Gleichungen:

$\sigma_{1} = \dfrac{\sigma_x + \sigma_y}{2} + \sqrt{\dfrac{\sigma_x - \sigma_y}{2})^2 + \tau_{xy}^2}$

$\sigma_{2} = \dfrac{\sigma_x + \sigma_y}{2} - \sqrt{\dfrac{\sigma_x - \sigma_y}{2})^2 + \tau_{xy}^2}$

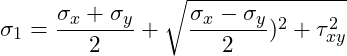
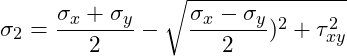
Bevor wir die Berechnung durchführen schauen wir uns zunächst den ebenen Spannungszustand mit positiven Spannungen an:

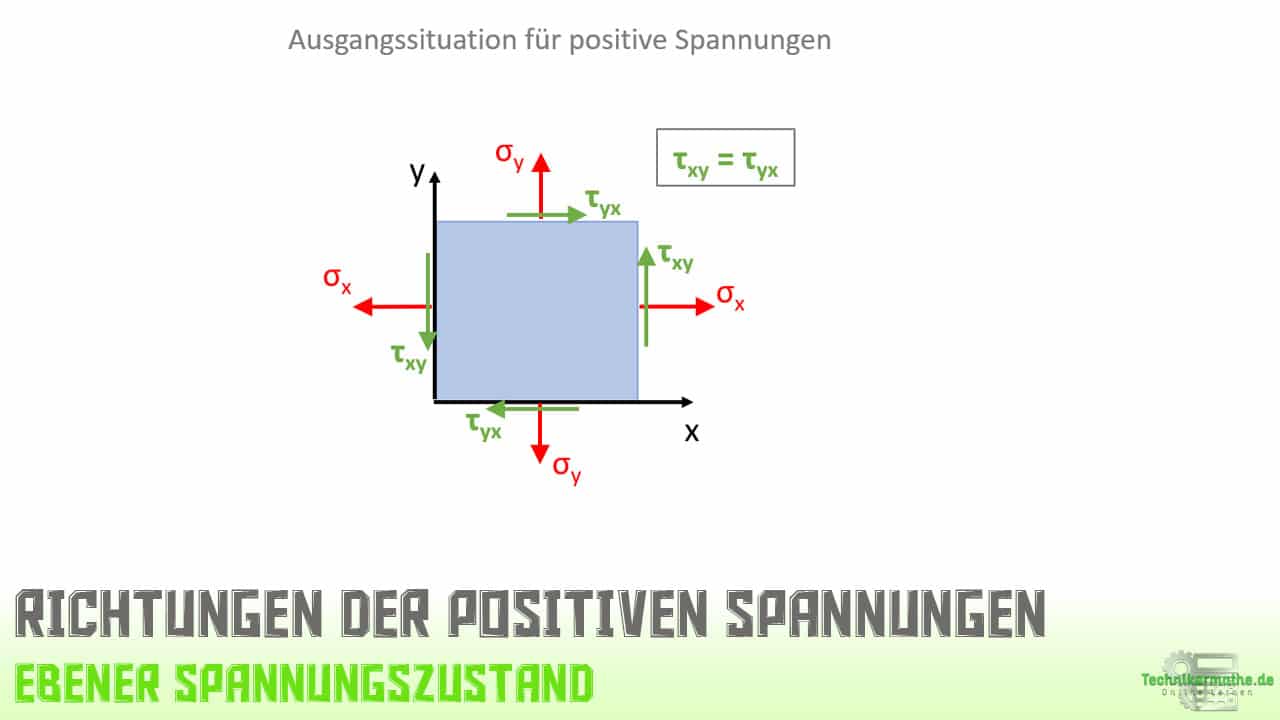
Spannungstransformation, ebener Spannungszustand, Nachhilfe Techniker, Hauptnormalspannungen, Beispiel — Spannungszustand für positive Spannungen

Wenn wir den positiven Spannungszustand mit der Aufgabenstellung vergleichen sehen wir, dass die Normalspannung in y-Richtung und die Schubspannung negativ sein muss, da diese genau entgegengesetzt wirken.

Es gilt also für das Beispiel:

$\sigma_x = 40 MPa$

$\sigma_y = -25 MPa$

$\tau_{xy} = -12 MPa$

Wir können nun die Hauptnormalspannungen berechnen:

$\sigma_{1} = \dfrac{40 MPa + (-25 MPa)}{2} + \sqrt{\dfrac{40 MPa - (-25 MPa)}{2})^2 + (-12 MPa)^2}$

$\sigma_{1} = 42,14 MPa$

$\sigma_{2} = \dfrac{40 MPa + (-25 MPa)}{2} - \sqrt{\dfrac{40 MPa - (-25 MPa)}{2})^2 + (-12 MPa)^2}$

$\sigma_{2} = -27,14 MPa$

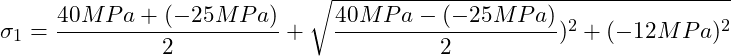
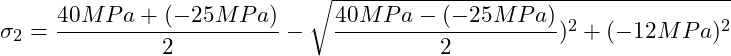
Wir haben die beiden Hauptnormalspannungen berechnet. Hierbei handelt es sich um die maximalen Normalspannungen, die innerhalb des betrachteten Bauteils mit dem in der Aufgabenstellung gegeben Spannungszustand auftreten können.

Wir wollen als nächstes wissen unter welchem Winkel die Hauptnormalspannungen auftreten. Wir sprechen hier von dem Winkel, um welchem das x,y-Koordinatensystem gedreht werden muss, damit die Hauptnormalspannungen gegeben sind. Diesen Winkel berechnest du mit der folgenden Gleichung:

$\alpha_{HN} = \frac{1}{2} \cdot \tan^{-1}(\dfrac{2 \cdot \tau_{xy}}{\sigma_x - \sigma_y})$

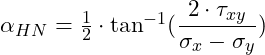
Wir setzen die gegeben Werte ein:

$\alpha_{HN} = \frac{1}{2} \cdot \tan^{-1}(\dfrac{2 \cdot (-12 MPa)}{40 MPa - (-25 MPa)}) = -10,13^\circ$

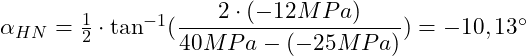
Es ergibt sich ein Winkel von α_HN = -10,13°. Das negative Vorzeichen zeigt an, dass die Drehung des Ausgangskoordinatensystems in einer Rechtsdrehung (mit dem Uhrzeigersinn) erfolgt. Wir müssen nun noch wissen, welche der obigen Hauptnormalspannungen in ξ-Richtung und η-Richtung wirkt. Dazu verwenden wir die Formeln für die Spannungstransformation:

$\sigma_{\xi} = \dfrac{\sigma_x + \sigma_y}{2} + \dfrac{\sigma_x - \sigma_y}{2} \cdot \cos(2 \alpha) + \tau_{xy} \cdot \sin(2 \alpha)$

$\sigma_{\eta} = \dfrac{\sigma_x + \sigma_y}{2} - \dfrac{\sigma_x - \sigma_y}{2} \cdot \cos(2 \alpha) - \tau_{xy} \cdot \sin(2 \alpha)$

Es reicht aus, wenn wir eine der Gleichungen verwenden. Wir setzen nun die gegeben Ausgangswerte ein und als Winkel die berechnete Hauptrichtung α_HN = -10,13°:

$\sigma_{\xi} = \dfrac{40 MPa+ (-25 MPa)}{2} + \dfrac{40 MPa- (-25 MPa}{2} \cdot \cos(2 \cdot (-10,13^\circ) + (-12 MPa) \cdot \sin(2 \cdot (-10,13^\circ)) = 42,14 MPa$

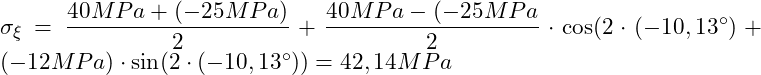
Bei einer Drehung des Ausgangskoordinatensystems um 10,13° in einer Rechtsdrehung ergibt sich eine Normalspannung in ξ-Richtung von 42,14 MPa. Dies entspricht der Hauptnormalspannung σ₁.

Merk’s dir!

Demnach zeigt die Hauptnormalspannung σ₁ in ξ-Richtung und die Hauptnormalspannung σ₂ in η-Richtung.

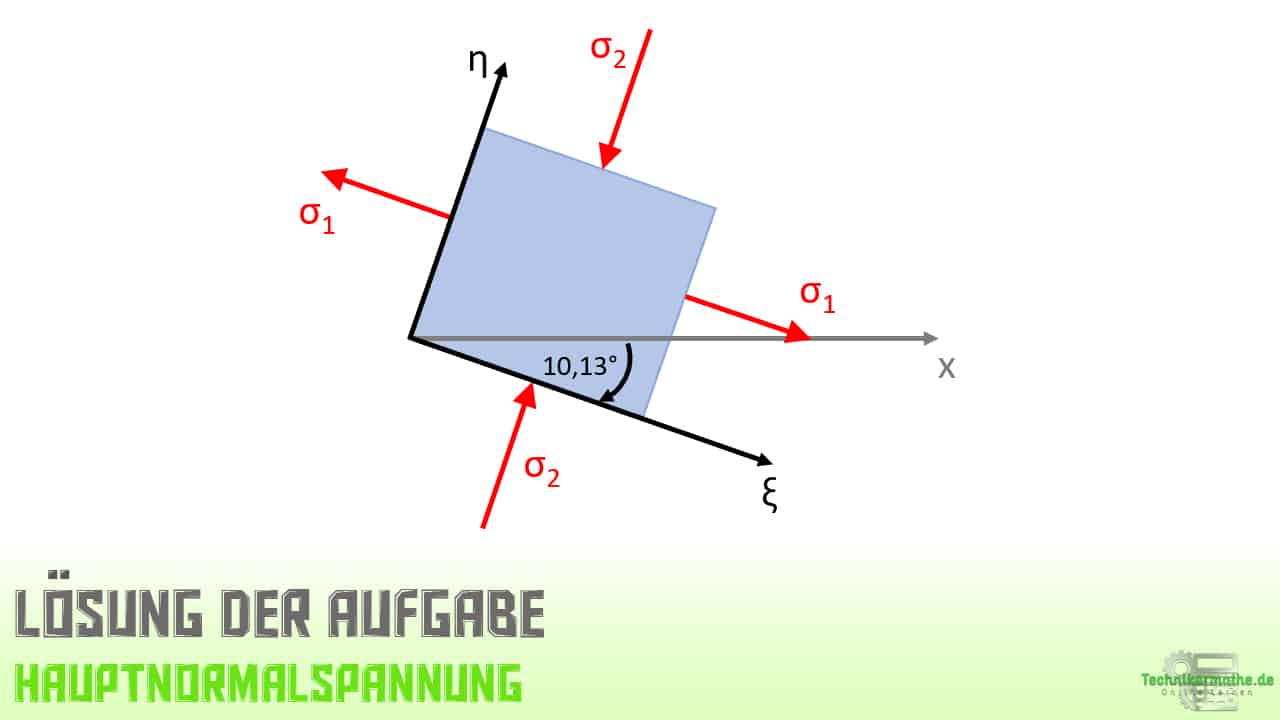
Hauptnormalspannung berechnen, Techniker Prüfungsvorbereitung, Hauptnormalspannungen, Hauptrichtung, Spannungen, Normalspannungen, Extremwerte — Lage der Hauptnormalspannungen

Schubspannungen werden zu Null

Beim Auftreten der Hauptnormalspannungen ist die Schubspannung Null. Das können wir anhand der Gleichung für die Spannungstransformation zeigen:

$\tau_{\eta \xi} = \tau_{\xi \eta} = - \dfrac{\sigma_x - \sigma_y}{2} \cdot \sin(2 \alpha) + \tau_{xy} \cdot \cos(2 \alpha)$

Einsetzen der Werte:

$\tau_{\eta \xi} = \tau_{\xi \eta} = - \dfrac{40 MPa - (-25 MPa)}{2} \cdot \sin(2 \cdot (-10,13^\circ)) + (-12 MPa) \cdot \cos(2 \cdot (-10,13^\circ)) = 0$

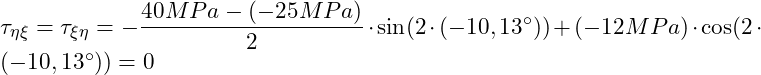
Tatsächlich ergibt sich für die obige Berechnung ein Wert von -0,00344.. . Dieser Wert resultiert daher, weil wir den Winkel von -10,13° gerundet einsetzen. Würden wir den Winkel ungerundet einsetzen, so ergäbe sich der Wert Null für die Schubspannung.

Was kommt als Nächstes?

In der folgenden Lerneinheit behandeln wir die Hauptschubspannungen und zeigen, wie diese berechnet werden.

Was gibt es noch bei uns?

Optimaler Lernerfolg durch tausende Übungsaufgaben

Quizfrage 1

“Wusstest du, dass unter jedem Kursabschnitt eine Vielzahl von verschiedenen interaktiven Übungsaufgaben bereitsteht, mit denen du deinen aktuellen Wissensstand überprüfen kannst?”

Alle Technikerschulen im Überblick

Zum Verzeichnis der Technikerschulen (Alles Rund um die Schulen) — Zum Verzeichnis der Technikerschulen

Kennst du eigentlich schon unser großes Technikerschulen-Verzeichnis für alle Bundesländer mit allen wichtigen Informationen (Studiengänge, Kosten, Anschrift, Routenplaner, Social-Media) ? Nein? – Dann schau einfach mal hinein:

Was ist Technikermathe?

Unser Dozent Jan erklärt es dir in nur 2 Minuten!

Oder direkt den > kostenlosen Probekurs < durchstöbern? – Hier findest du Auszüge aus Alle Onlinekurse Technikermathe!

Geballtes Wissen in derzeit 26 Kursen

Hat dir dieses Thema gefallen? – Ja? – Dann schaue dir auch gleich die anderen Themen zu den Kursen

WT3 (Werkstoffprüfung) und
TM1 (Technische Mechanik – Statik) an.

Lerne nun erfolgreich mit unserem Onlinekurs Technische Mechanik 1 — TM1 (Technische Mechanik)

Lerne nun erfolgreich mit unserem Onlinekurs Werkstofftechnik 3 — WT3 (Werkstoffprüfung)

Perfekte Prüfungsvorbereitung für nur 14,90 EUR/Jahr pro Kurs

++ Günstiger geht’s nicht!! ++

Oder direkt Mitglied werden und Alle unsere Onlinekurse (inkl. Webinare + Unterlagen) sichern ab 7,40 EUR/Monat ++ Besser geht’s nicht!! ++