Hauptachsen sind Achsen, die durch den Schwerpunkt einer Fläche bzw. eines Querschnitts verlaufen und für die das Deviationsmoment verschwindet (= zu Null wird). Die zu den Hauptachsen dazugehörigen Flächenträgheitsmomente werden als Hauptträgheitsmomente bezeichnet.
Hauptachsen und Hauptträgheitsmoment – Erklärung
Achsen, die durch den Schwerpunkt einer Fläche bzw. eines Querschnitts verlaufen und für die das Deviationsmoment verschwindet, werden als Hauptachsen bezeichnet. Die zu den Hauptachsen dazugehörigen Flächenträgheitsmomente heißen Hauptträgheitsmomente. Die Hauptträgheitsmomente sind nichts anderes als die Extremwerte der Flächenträgheitsmomente, also diejenigen Werte, bei welchen die Flächenträgheitsmomente für den betrachteten Querschnitt maximal bzw. minimal werden.
Hauptachsen
Wir wissen bereits aus den vorangegangenen Lerneinheiten, dass das Deviationsmoment verschwindet, wenn mindestens eine der gegebenen Achsen eine Symmetrieachse darstellt. Was ist aber, wenn keine der Achsen eine Symmetrieachse darstellt, wie in der folgenden Grafik zu sehen ist:
In der obigen Grafik siehst du, dass keine der beiden Achsen eine Symmetrieachse darstellt. Damit wird das Deviationsmoment Iyz ungleich Null.
Es existieren aber auch für den obigen Querschnitt zwei senkrecht aufeinander stehende Achsen, für welche das Deviationsmoment verschwindet (Iyz = 0). Diese beiden Achsen werden Hauptachsen genannt.
Zur Berechnung der Lage der Hauptachsen (=Hauptrichtung) kannst du die folgende Gleichung heranziehen:
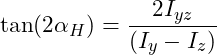
Die Hauptrichtung ist derjenigen Winkel, bei welchen die Hauptachsen gegeben sind.
Hast du bereits einen Querschnitt gegeben, bei welchem mindestens eine der gegebenen y,z – Achsen eine Symmetrieachse darstellt, so sind beide Achsen (y- und z-Achse) bereits Hauptachsen des Querschnitts.
Hauptträgheitsmomente
Die zu den Hauptachsen dazugehörigen Flächenträgheitsmomente heißen Hauptträgheitsmomente.
Die Hauptträgheitsmomente sind nichts anderes als die Extremwerte der Flächenträgheitsmomente, also derjenige Wert, bei welchem die Flächenträgheitsmomente für den betrachteten Querschnitt maximal bzw. minimal werden.
Zur Berechnung der Hauptträgheitsmomente kannst du die folgende Gleichung heranziehen (analog zu den Hauptspannungen):
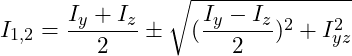
Betrachten wir ein Beispiel zur Berechnung.
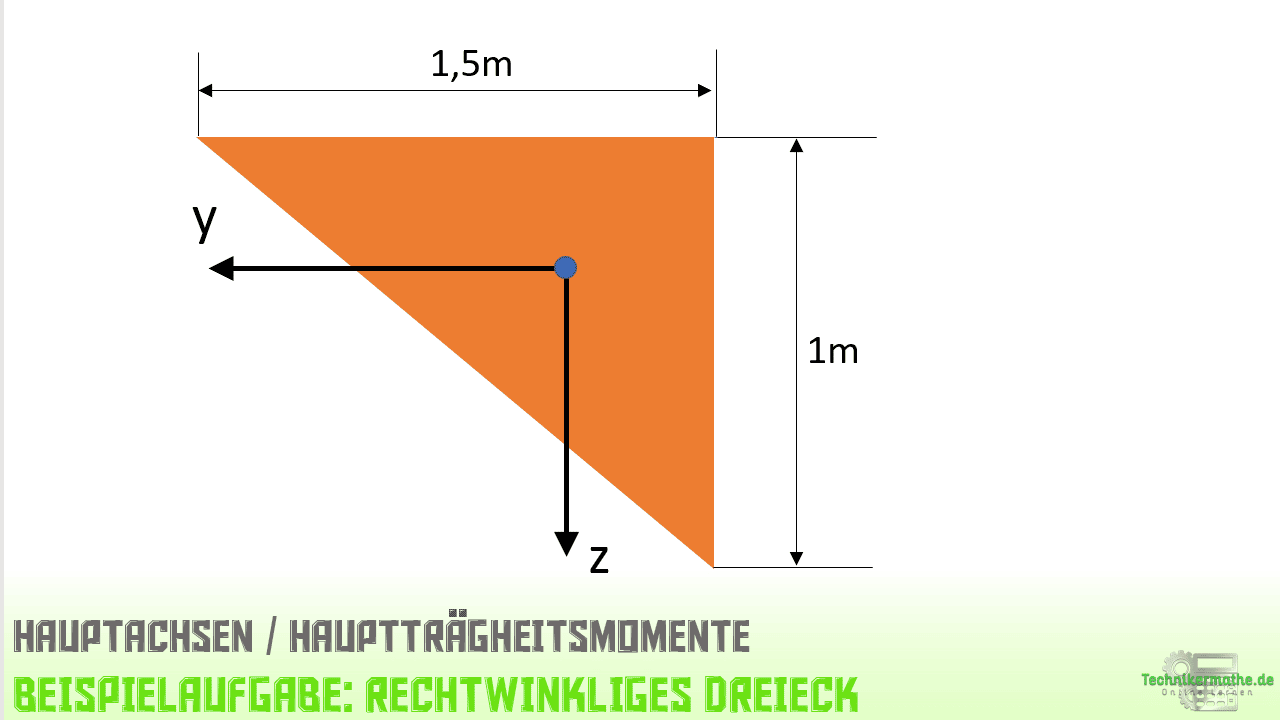
Aufgabe: Hauptachsen & Hauptträgheitsmomente
Hauptachsen
Weder die y-Achse noch die z-Achse sind Symmetrieachsen des gegebenen Querschnitts. Demnach sind diese Achsen keine Hauptachsen des Querschnitts. Zur Berechnung der Lage der Hauptachsen, können wir die folgende Gleichung heranziehen:
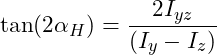
Zunächst benötigen wir hierzu die axialen Flächenträgheitsmomente Iy und Iz sowie das Deviationsmoment Iyz für das gegebene y,z-Koordinatensystem. Diese können wir Tabellenwerken entnehmen.
Für ein Dreieck gelten die folgenden Formeln:
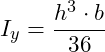
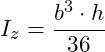
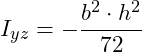
Im nächsten Schritt setzen wir die in der Aufgabenstellung gegebenen Abmessungen in die obigen Gleichungen ein. Es gilt h = 1m und b = 1,5m:
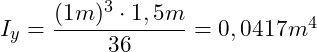
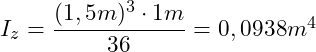
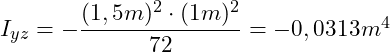
Wir können nun die gegebenen Werte in die Gleichung einsetzen:
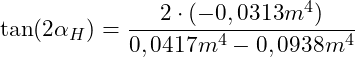
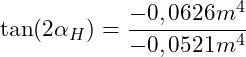
![]()
Nach dem Winkel ![]() auflösen:
auflösen:
![]()
![]()
![]()
![]()
![]()
Mit dem Taschenrechner das Ergebnis berechnen:
![]()
Die Hauptachsen treten unter einem Winkel von 25,11° auf. Zur Bestimmung der Hauptachsen wird das y,z-Koordinatensystem um 25,11° in einer Linksdrehung gedreht. Eine Linksdrehung ist gegeben, weil der berechnete Winkel positiv ist. Bei einem negativen Winkel wird das y,z-Koordinatensystem in einer Rechtsdrehung gedreht.
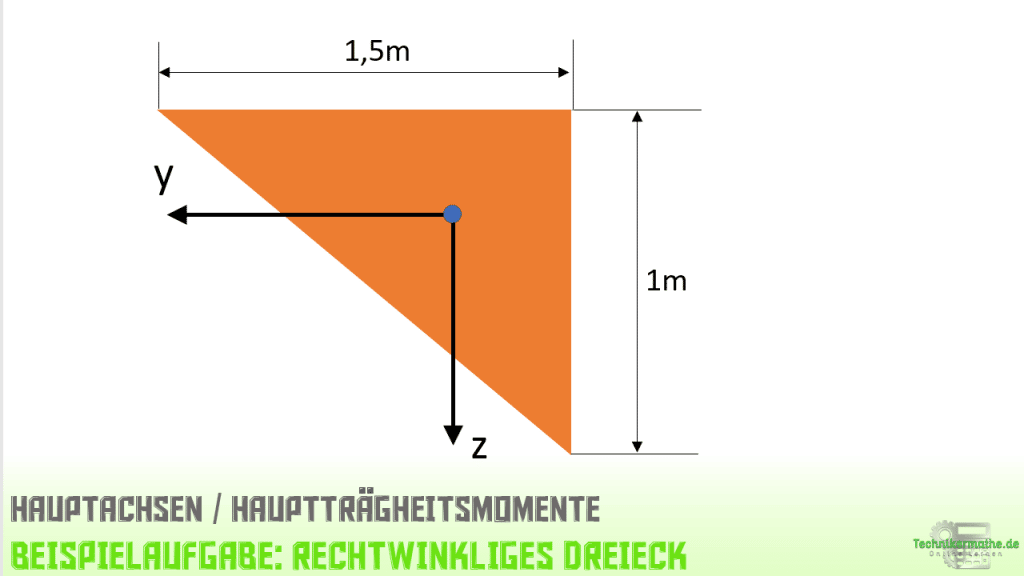
In der folgenden Grafik siehst du die Lage der Hauptachsen für das gegebene rechtwinklige Dreieck:
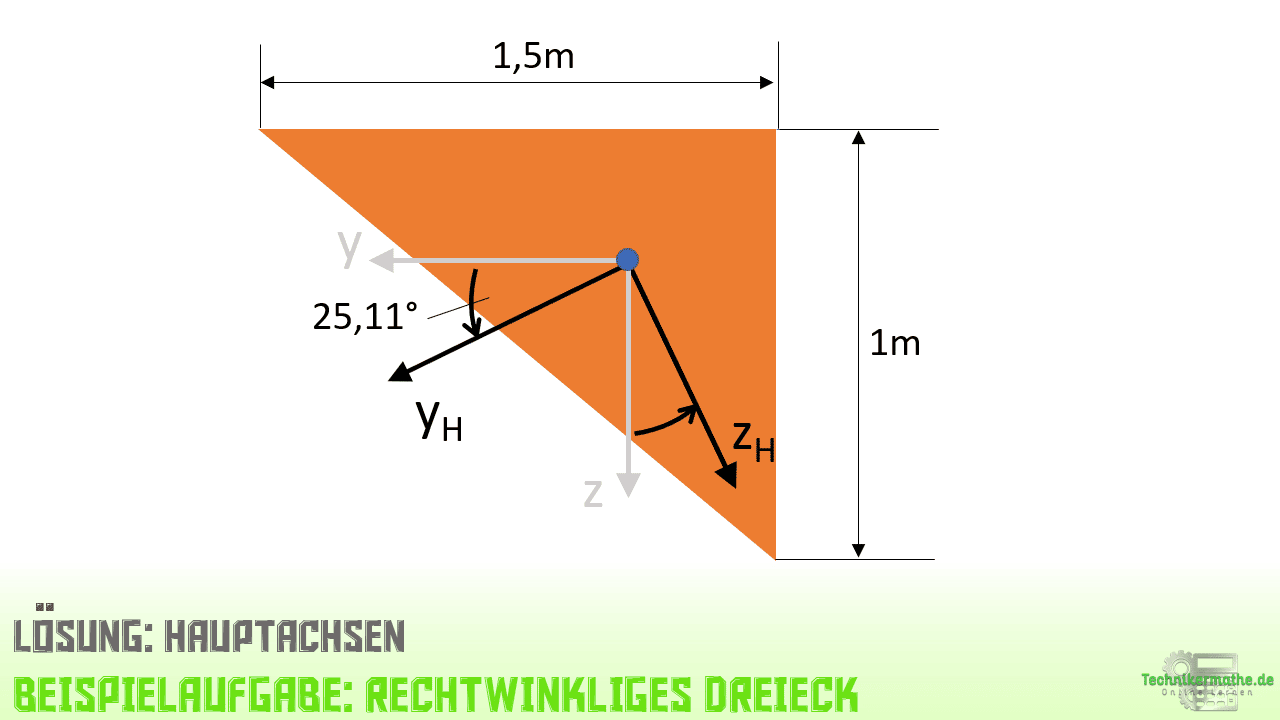
In der obigen Grafik siehst du die Lage der Hauptachsen yH und zH. Das Ausgangskoordinatensystem haben wir in einer Linksdrehung mit dem Winkel 25,11° gedreht.
Hauptträgheitsmomente
Es gibt genau eine bestimmte Stellung, bei welcher die axialen Flächenträgheitsmomente maximal bzw. minimal werden sowie das Deviationsmoment Iyz verschwindet. Und zwar genau dann, wenn die Hauptachsen gegeben sind.
Wir berechnen nun also die Extremwerte der Flächenträgheitsmomente für das gerade ermittelte yH,zH-Koordinatensystem.
Zur Berechnung der Hauptträgheitsmomente ziehen wir die folgende Gleichung heran:
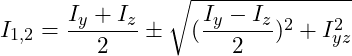
Auch hier setzen wir wieder die Flächenträgheitsmomente Iy und Iz sowie das Deviationsmoment Iyz (aus Tabellenwerken entnommen, siehe oben) heran:
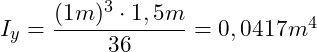
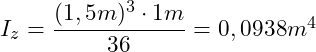
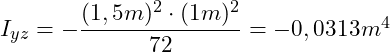
Das Flächenträgheitsmoment Iz ist größer, als das Flächenträgheitsmoment Iy. Demnach berechnen wir im Folgenden das Maximum der starken Achse (Drehung Iz = I1) und das Minimum der “schwächeren” Achse (Drehung Iy = I2).
Einsetzen der Werte in die Gleichung zur Berechnung der Hauptträgheitsmomente:
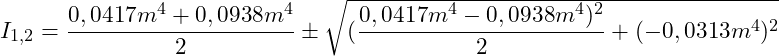
![]()
![]() Drehung Iz um 25,11°
Drehung Iz um 25,11°
![]() Drehung Iy um 25,11°
Drehung Iy um 25,11°
Der maximale Wert von I1 = 0,1286m4 gehört zur Hauptachse yH, der minimale Wert von I2 = 0,007m4 gehört zur Hauptachse zH.
In der folgenden Lerneinheit schauen wir uns den Satz von Steiner zur Berechnung der Flächenträgheitsmomente für parallele Achse sowie für zusammengesetzte Flächen.
Was gibt es noch bei uns?
Optimaler Lernerfolg durch tausende Übungsaufgaben

Quizfrage 1
“Wusstest du, dass unter jedem Kursabschnitt eine Vielzahl von verschiedenen interaktiven Übungsaufgaben bereitsteht, mit denen du deinen aktuellen Wissensstand überprüfen kannst?”
Was ist Technikermathe?
Unser Dozent Jan erklärt es dir in nur 2 Minuten!
Oder direkt den > kostenlosen Probekurs < durchstöbern? – Hier findest du Auszüge aus Alle Onlinekurse Technikermathe!
Geballtes Wissen in derzeit 26 Kursen
Hat dir dieses Thema gefallen? – Ja? – Dann schaue dir auch gleich die anderen Themen zu den Kursen
WT3 (Werkstoffprüfung) und
TM1 (Technische Mechanik – Statik) an.


Perfekte Prüfungsvorbereitung für nur 14,90 EUR/Jahr pro Kurs
++ Günstiger geht’s nicht!! ++
Oder direkt Mitglied werden und Alle unsere Onlinekurse (inkl. Webinare + Unterlagen) sichern ab 7,40 EUR/Monat ++ Besser geht’s nicht!! ++
Social Media? - Sind wir dabei!
Dein Technikermathe.de-Team