⚙️TM2 | Gewicht an zwei Seilen [Grundlagen, Erklärung, Videoclips, Aufgaben & Tipps]

In dieser Prüfungsaufgabe betrachten wir ein Gewicht, dass an zwei Seilen befestigt ist. Wir wollen hier die Seilkräfte berechnen, die Längenänderung der Seile und die daraus resultierende vertikale Absenkung des Gewichts.

In dieser Lerneinheit betrachten wir eine Prüfungsaufgabe zur Bestimmung der Seilkräfte und der Verschiebung infolge der Seilverlängerung.

Mehr zu diesem Thema und der Mechanik findest du im Kurs: TM2 – Festigkeitslehre.

Oder lieber mit den Grundlagen starten? Alles dazu findest du im Kurs: Ma1-Grundlagen der Mathematik

Was bedeutet „Gewicht an zwei Seilen“?

Wenn ein Gewicht an zwei Seilen hängt, wirken Kräfte entlang der Seile, die das Gewicht in einem Gleichgewichtszustand halten. Ziel ist es hier die unbekannten Seilkräfte zu berechnen. Diese können wir berechnen, indem wir die Kräfte zerlegen und anschließend die Gleichgewichtsbedingungen anwenden. Zusätzlich betrachten wir die Längenänderung der Seile infolge des angehängten Gewichts und die damit verbundene Absenkung.

Aufgaben | Gewicht an zwei Seilen

Aufgabe 1: Gewicht an zwei Seilen

Aufgabenstellung

Gewicht an Seilen, Seilkräfte, Gleichgewichtsbedingungen, Seilkräfte berechnen, Beispiel, Absenkung, Verschiebung, Längenänderung — Beispiel: Seilkräfte und Absenkung bestimmen

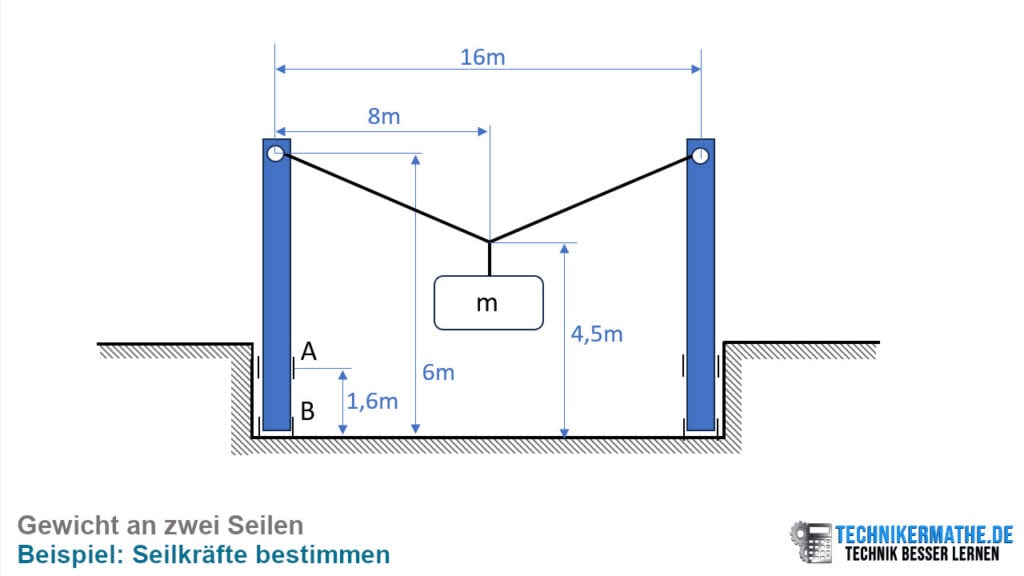
Gegeben seien zwei an Mauern verankerte Masten, an denen zwei Seile befestigt sind. Ein Gewicht mit der Masse m = 140kg ist mittig an den zwei Seilen befestigt.

a) Bestimme die Seilkräfte.

b) Um welches Maß senkt sich die Last im Vergleich zum unbelasteten Zustand ab? Das Seil besteht aus 8 Litzen mit je 17 Drähten von 0,75mm Durchmesser (E-Modul: 85.000 N/mm²). Die Biegung der Masten soll unberücksichtigt bleiben.

Lösung a) Seilkräfte

Die beiden Seile sowie das Gewicht treffen sich alle in einem einzigen Punkt. Damit haben wir hier ein zentrales Kräftesystem gegeben. Wir können nun diesen gemeinsamen Punkt, der sich im Gleichgewicht befindet, freischneiden. Wir tragen dann die Seilkräfte (also Zugkräfte) und die Gewichtskraft an:

Gewicht an zwei Seilen, Gewichtskraft, Seilkräfte, Seilkraft, Freischnitt, Absenkung, Längenänderung, — Freischnitt

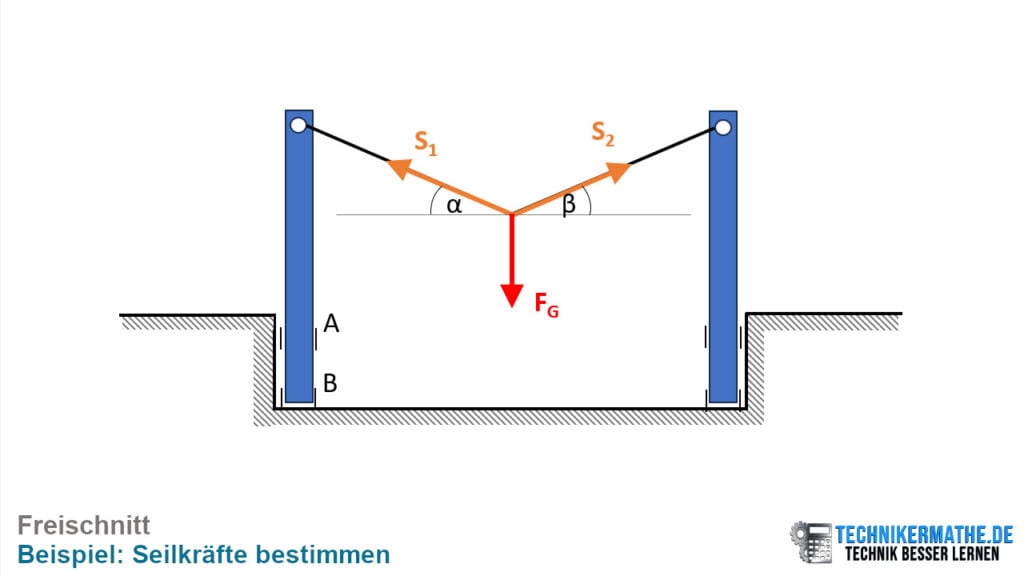
Der Betrag und die Richtung der Gewichtskraft sind gegeben:

$F_G = m \cdot g = 140kg \cdot 9,81 \frac{m}{s^2} = 1.373,4 N$

Die beiden Seilkräfte können wir in ihre x- und y-Komponenten zerlegen, so dass wir die Gleichgewichtsbedingungen anwenden können, um die Seilkräfte zu berechnen. Da sich alle drei Kräfte in einem einzigen Punkt schneiden, können wir hier die Gleichgewichtsbedingung in x-Richtung und die Gleichgewichtsbedingung in y-Richtung anwenden. Die Momentengleichgewichtsbedingung fällt weg, da keine Momente wirken.

Merk’s dir!

Die drei Kräfte liegen alle in dem gemeinsame Angriffspunkt. Damit ist schonmal per Definition ein zentrales Kräftesystem gegeben. Momente werden durch die drei Kräfte auf den Angriffspunkt nicht ausgeübt.

Wir führen die Kräftezerlegung durch, damit wir die Gleichgewichtsbedingungen anwenden können:

Gewicht an Seilen, Seilkräfte, Kräftezerlegung — Kräftezerlegung

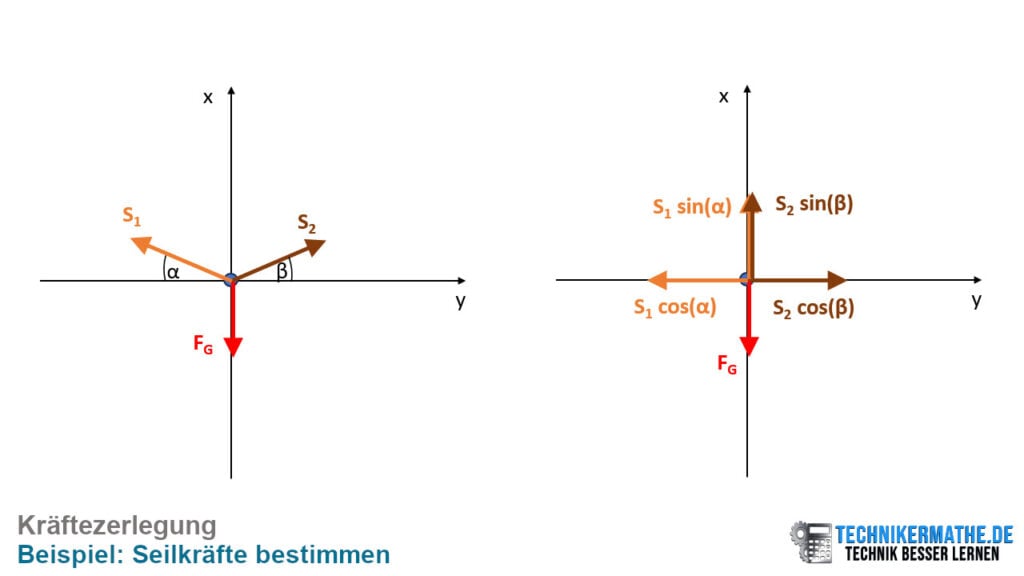
Wir suchen noch die Winkel α und β. Diese können wir aus der Geometrie mittels Trigonometrie am rechtwinkligen Dreieck wie folgt berechnen:

Gewicht an zwei Seilen, Trigonometrie, Seilkräfte, Längenänderung, Beispiel, Absenkung — Trigonometrie am rechtwinkligen Dreieck

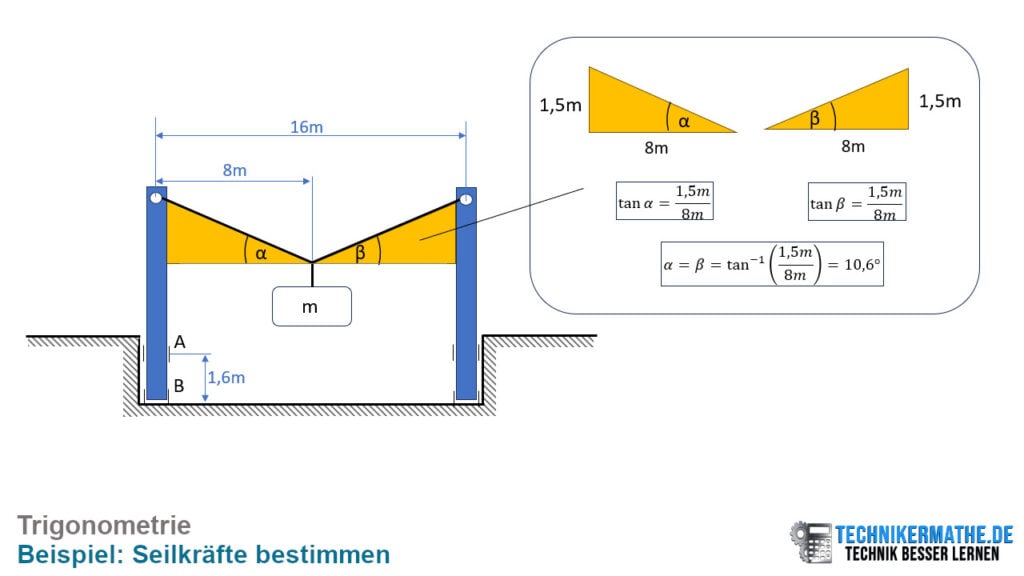
In unserem Beispiel ist die Aufhängung genau mittig und deswegen sind die Winkel α und β gleich groß. Das Gewicht m verteilt sich damit auf die beiden Seilkräfte zu gleichen Teilen. Damit sind die beiden Seilkräfte S₁ und S₂ gleich groß.

Es gilt also:

$S_1 = S_2$

Wir können als nächstes die beiden Gleichgewichtsbedingungen der Ebene für ein zentrales Kräftesystem anwenden, um die unbekannten Seilkräfte (bzw. die unbekannte Seilkraft) zu bestimmen.

Horizontale Gleichgewichtsbedingung

$\rightarrow:$

$\sum F_{ix} = 0:$

(1) $S_2 \cdot \cos(\beta) - S_1 \cdot \cos(\alpha) = 0$

Vertikale Gleichgewichtsbedingung

$\uparrow:$

$\sum F_{iy} = 0$ :

(2) $-F_G + S_1 \cdot \sin(\alpha) + S_2 \cdot \sin(\beta) = 0$

Wir lösen nun beide Gleichgewichtsbedingungen nach einer Unbekannten (S₁ oder S₂) auf und setzen diese gleich:

$S_2 = \frac{S_1 \cdot \cos(\alpha)}{\cos(\beta)}$

$S_2 = \frac{F_G - S_1 \cdot \sin(\alpha)}{\sin(\beta)}$

Gleichsetzen:

$\frac{S_1 \cdot \cos(\alpha)}{\cos(\beta)} = \frac{F_G - S_1 \cdot \sin(\alpha)}{\sin(\beta)}$

Wir können nun hier die Vereinfachungen einsetzen. Es gilt:

$\beta = \alpha$

Damit erhalten wir:

$\frac{S_1 \cdot \cos(\alpha)}{\cos(\alpha)} = \frac{F_G - S_1 \cdot \sin(\alpha)}{\sin(\alpha)}$

$S_1 = \frac{F_G}{\sin(\alpha)} - S_1$

$2 \cdot S_1 = \frac{F_G}{\sin(\alpha)}$

$S_1 = \frac{1}{2} \frac{F_G}{\sin(\alpha)}$

$S_1 = \frac{1}{2} \frac{1.373,4 N}{\sin(10,6^\circ)} = 3.733,1 N$

Da S₁ gleich S₂, erhalten wir für die andere Stabkraft denselben Wert:

$S_2 = 3.733,1 N$

Ob die Berechnung richtig war, können wir anhand der Parallelogrammkonstruktion herausfinden, indem wir den Kosinussatz anwenden:

$F_R = F_H = F_G = \sqrt{S_1^2 + S_2^2 - 2 \cdot S_1 \cdot S_2 \cdot \cos(\gamma)}$

$F_G = \sqrt{(3.733,1 N)^2 + (3.733,1 N)^2 - 2 \cdot 3.733,1 N \cdot 3.733,1 N \cdot \cos(10,6^\circ)}$

$F_G = 1.373,4 N$

Lösung b) Absenkung des Gewichts

Als nächstes wollen wir die Absenkung des Gewichts bestimmen. Infolge des angreifenden Gewichts verlängern sich die beiden Stahldrähte. Wir berechnen also erst die Längenänderung und dann die vertikale Absenkung aus der Geometrie.

Die Längenänderung kann mittels der folgenden Gleichung berechnet werden:

$\Delta l = \frac{F \cdot L}{EA}$

Die in der Formel angegeben Kraft F ist die Kraft entlang des Seils, also die oben berechnete Seilkraft. Wir berechnen die Längenänderung für das Seil S₁. Dieselbe Längenänderung erfährt auch das Seil S₂, da die Seilkräfte, Längen und E-Module beider Seile identisch sind.

$\Delta l = \frac{S_1 \cdot L}{EA}$

Wir haben alle Werte außer die Fläche A und die Länge L gegeben. Diese können wir aus den Angaben der Aufgabenstellung berechnen.

Fläche berechnen

In der Aufgabenstellung haben wir ein Seil mit 8 Litzen mit je 17 Drähten gegeben:

Grafik

Da es sich hierbei um kreisförmige Drähte handelt, können wir die Fläche eines einzelnen Drahtes mit der folgenden Formel berechnen:

$A_{Draht} = \pi \cdot r^2$

Der Durchmesser je Draht beträgt 0,75mm. Der Radius damit r = 0,375mm:

$A_{Draht} = \pi \cdot (0,375mm)^2 = 0,442mm^2$

Wir haben insgesamt pro Litze 17 Drähte gegeben:

$A_{Litze} = 0,442mm^2 \cdot 17 = 7,514mm^2$

Wir haben insgesamt 8 Litzen gegeben:

$A_{Seil} = 7,514mm^2 \cdot 8 = 60,112mm^2$

Länge und Längenänderung berechnen

Als nächstes berechnen wir die Länge des Seils aus der Geometrie wie folgt:

Länge berechnen, Seil, Gewicht an Seilen, Längenänderung, Seillänge, Gewicht an zwei Seilen, Seilkräfte — Längenänderung berechnen

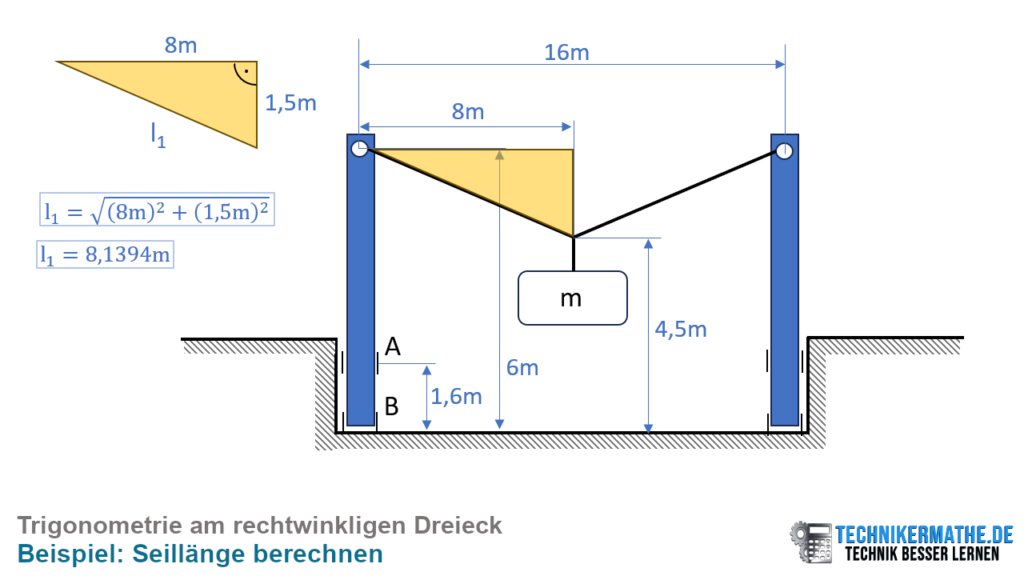
Wir können die Länge mittels Satz des Pythagoras berechnen. Dabei ist die Länge des Seils die Hypotenuse des oben konstruierten rechtwinkligen Dreiecks:

$L = \sqrt{8m)^2 + (1,5m)^2} = 8,1394m$

Nachdem wir die Querschnittsfläche und Länge des Seils bestimmt haben, können wir als nächstes die Längenänderung berechnen:

$\Delta l = \frac{S_1 \cdot L}{EA}$

Der Elastizitätsmodul ist in der Einheit N/mm² angegeben. Da wir die Länge in Meter und die Fläche in mm² gegeben haben, müssen wir entweder die Länge in mm oder den Elastizitätsmodul in N/m² und die Fläche in m² umrechnen. Wir wählen die Länge in mm:

$L = 8,1394m = 8.139,4mm$

Wir können nun alle Werte einsetzen:

$\Delta l = \frac{3.733,1 N \cdot 8.139,4mm}{85.000 \frac{N}{mm} \cdot 60,112mm^2}$

$\Delta l = 5,9468mm$

Die Länge des Seils S₁ verlängert sich um 5,9468mm.

Die Länge des Seils S₂ verlängert sich ebenfalls um 5,9468mm.

Alternative Berechnung der Längenänderung über die Spannung und Dehnung (Hooksche Gesetz)

Alternativ können wir die Längenänderung auch über das Hooksche Gesetz bestimmen:

$\sigma= \epsilon \cdot E$ Hooksche Gesetz

$\epsilon= \frac{\sigma}{E}$

Die Normalspannung berechnen wir zu:

$\sigma = \frac{F}{A} = \frac{S_1}{A}$

$\sigma = \frac{3.733,1 N}{60,112mm^2} = 62,1024 \frac{N}{mm^2}$

Einsetzen in das Hooksche Gesetz aufgelöst nach der Dehnung:

$\epsilon= \frac{62,1024 \frac{N}{mm^2}}{85.000 \frac{N}{mm^2}}$

$\epsilon = 0,000731$

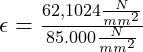
In Prozent: 0,0731 %

Die Dehnung des Seils erfolgt um 0,0731%.

Mittels der Ausgangslänge des Seils können wir die Längenänderung berechnen:

$\Delta l = L \cdot \epsilon = 8.139,4mm \cdot 0,000731 = 5,95mm$

Absenkung des Gewichts

Nachdem wir die Längenänderungen der beiden Seile berechnet haben, können wir die Absenkung des Gewichts bestimmen. Dazu benötigen wir wieder die Geometrie:

Absenkung, Längenänderung, Verschiebung, Gewicht, Seile, Geometrie, Verschiebungsplan, Verschiebung, Absenkung Gewicht, vertikale Verschiebung, Verschiebung eines Knotens — Absenkung bestimmen

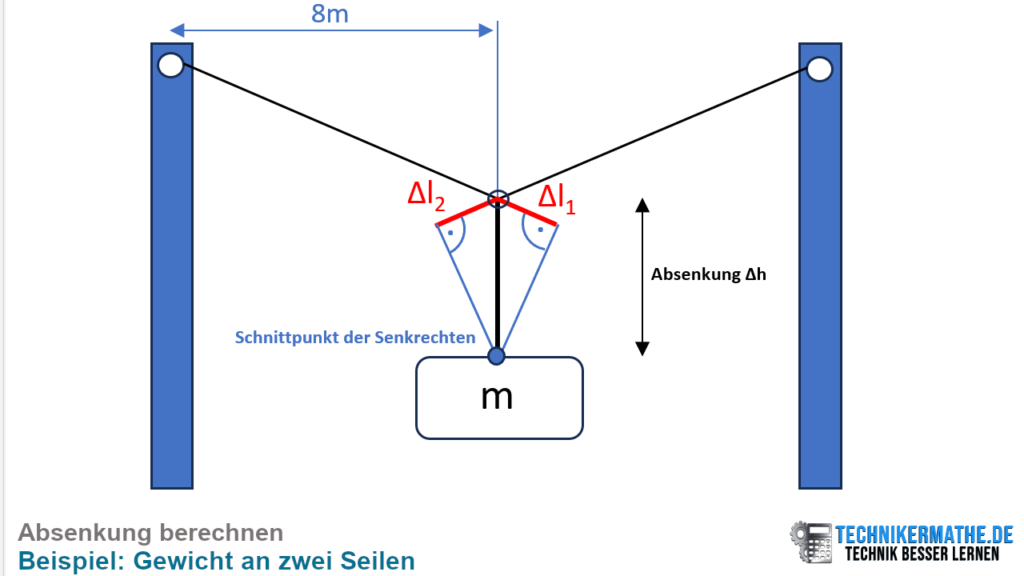
In der obigen Grafik haben wir das Seil S₁ verlängert um $\Delta l_1$ und das Seil S₂ verlängert um $\Delta l_2$ eingezeichnet (wobei die Längenänderung für beide Seile gleich ist). Danach haben wir von den verlängerten Seilen eine dazu orthogonale Linie (im 90°-Winkel) gezogen. Dort, wo sie sich diese beiden Linien treffen, liegt der neue gemeinsame Angriffspunkt, der sich infolge des angreifenden Gewichts m ergibt.

Die Längenänderungen wurden innerhalb der Grafik sehr groß eingezeichnet, so dass sich die neue Lage des Punktes ist in der Grafik sehr weit entfernt vom ursprünglichen Punkt ergibt. Das dient dazu, die Verschiebung besser veranschaulichen können. Die tatsächliche Verschiebung des Punktes ist sehr klein und wäre damit kaum sichtbar und damit für geometrische Berechnungen ungeeignet.

Die mittige Ausrichtung des Gewichts (jeweils im Abstand von 6m zu den Masten) ändert sich hier nicht, da die Längenänderungen der beiden Seile identisch sind. Damit müssen wir nur den vertikalen Abstand (die Absenkung des Gewichts) berechnen.

Das können wir indem wir auch hier wieder die Geometrie betrachten:

Absenkung berechnen, Seil, Gewicht an zwei Seilen, Längenänderung, Verschiebung, Knoten, — Absenkung bestimmen

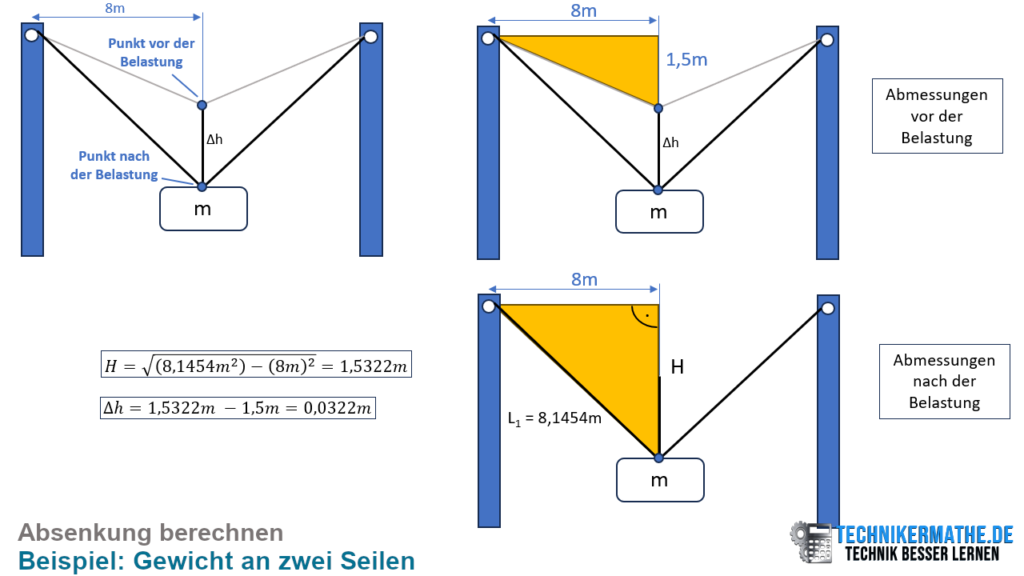
In der obigen Grafik sehen wir (stark vergrößert eingezeichnet) die Absenkung des Gewichts. Wir suchen den vertikalen Abstand des Punktes. Vor der Belastung war der Punkt (an dem das Gewicht hängt) bei h = 1,5m (von dem oberen Punkt des Masten aus gesehen) gegeben. Nach der Belastung befindet sich der Punkt in einem Abstand von H vom oberen Punkt des Masten betrachtet. Diesen Abstand berechnen wir mittels der Trigonometrie am rechtwinkligen Dreieck.

Wir betrachten dazu die untere Grafik. Wir haben die Hypotenuse gegeben. Diese ist nichts anderes als die neue Länge des Seils S₁. Die neue Länge ist die Ausgangslänge addiert mit der Längenänderung:

$L_{1, neu} = L_1 + \Delta l_1 = 8.139,4mm + 5,95mm = 8145,35mm = 8,1454m$

Wir haben zudem den horizontalen Abstand vom Masten zur Aufhängung mit 8m gegeben (dieser ändert sich hier nicht, da die Längenänderungen der beiden Seile gleich groß ist). Wir können hier also den Satz des Pythagoras anwenden:

$L_{1, neu}^2 = (8m)^2 + H^2$

Auflösen nach der gesuchten Größe H:

$H^2 = L_{1, neu}^2 - (8m)^2$

$H = \sqrt{L_{1, neu}^2 - (8m)^2}$

$H = \sqrt{8,1454m^2 - (8m)^2}$

$H = 1,5322m$

Der neue Punkt befindet sich also in einer Höhe (ausgehend vom oberen Masten) von 1,5322m. Wir können nun die Differenz aus der alten Höhe (1,5m) und der neue Höhe bilden:

$\Delta h = 1,5322m - 1,5m = 0,0322m$

Damit senkt sich das Gewicht nach der Belastung um 0,0322m ab.

Anwendung in der Praxis

Diese Methoden werden oft in der Bauingenieurwesen, Architektur und vielen anderen Bereichen angewendet, um die Stabilität und das Gleichgewicht von Strukturen zu berechnen, die durch Seile oder Kabel gestützt werden.

Mögliche Fragestellungen | Häufig gestellte Fragen (FAQs)

1. Was ist die Gewichtskraft?

Die Gewichtskraft ist die Kraft, die auf einen Körper aufgrund der Schwerkraft wirkt, berechnet durch $F_G = m \cdot g$ .

2. Wie werden die Seilkräfte zerlegt?

Seilkräfte werden in horizontale und vertikale Komponenten zerlegt, basierend auf den Winkeln, die die Seile mit der Horizontalen bilden.

3. Was sind die Gleichgewichtsbedingungen?

Die Summe der horizontalen Kräfte und die Summe der vertikalen Kräfte müssen jeweils null sein, damit das System im Gleichgewicht ist.

4. Wie löst man das Gleichungssystem?

Man stellt Gleichungen für die horizontalen und vertikalen Kräfte auf und löst diese nach den unbekannten Seilkräften auf.

5. Warum sind diese Berechnungen wichtig?

Diese Berechnungen sind wichtig für das Verständnis und die Planung von stabilen Strukturen, bei denen Kräfte durch Seile übertragen werden.

Zusammenfassung

Die Berechnung der unbekannten Seilkräfte erfordert die Kenntnis über die Kräftezerlegung und die Anwendung von Gleichgewichtsbedingungen.

Durch das Erstellen eines Freikörperdiagramms, das Zerlegen der Seilkräfte und das Aufstellen und Lösen von Gleichungen können die Kräfte in den Seilen bestimmt werden.

Die Berechnung der Längenänderung und die Einzeichnung dieser in einen Verschiebeplan sind notwendige Voraussetzung, um die vertikale Absenkung des Gewichts anhand der Geometrie bestimmten zu können.

Was kommt als Nächstes?

In der folgenden Lerneinheit starten wir mit der Mengenlehre.

Was gibt es noch bei uns?

Optimaler Lernerfolg durch tausende Übungsaufgaben

Übungsbereich (Demo) - Lerne mit mehr als 4000 Übungsaufgaben für deine Prüfungen — Übungsbereich (Demo) – Lerne mit mehr als 4000 Übungsaufgaben für deine Prüfungen

Quizfrage 1

“Wusstest du, dass unter jedem Kursabschnitt eine Vielzahl von verschiedenen interaktiven Übungsaufgaben bereitsteht, mit denen du deinen aktuellen Wissensstand überprüfen kannst?”

Alle Technikerschulen im Überblick

Zum Verzeichnis der Technikerschulen (Alles Rund um die Schulen) — Zum Verzeichnis der Technikerschulen

Kennst du eigentlich schon unser großes Technikerschulen-Verzeichnis für alle Bundesländer mit allen wichtigen Informationen (Studiengänge, Kosten, Anschrift, Routenplaner, Social-Media) ? Nein? – Dann schau einfach mal hinein:

Was ist Technikermathe?

Unser Dozent Jan erklärt es dir in nur 2 Minuten!

Oder direkt den > kostenlosen Probekurs < durchstöbern? – Hier findest du Auszüge aus jedem unserer Kurse!

Geballtes Wissen in derzeit 26 Kursen

Hat dir dieses Thema gefallen? – Ja? – Dann schaue dir auch gleich die anderen Themen zu den Kursen

WT3 (Werkstoffprüfung) und
TM1 (Technische Mechanik – Statik) an.

Lerne nun erfolgreich mit unserem Onlinekurs Technische Mechanik 1 — TM1 (Technische Mechanik)

Lerne nun erfolgreich mit unserem Onlinekurs Werkstofftechnik 3 — WT3 (Werkstoffprüfung)

Perfekte Prüfungsvorbereitung für nur 14,90 EUR/Jahr pro Kurs

++ Günstiger geht’s nicht!! ++

Oder direkt Mitglied werden und Zugriff auf alle 26 Kurse (inkl. Webinare + Unterlagen) sichern ab 7,40 EUR/Monat ++ Besser geht’s nicht!! ++