TM2 – Flächenträgheitsmomente mittels Integration [Formeln, Video, Berechnung]

Das Flächenträgheitsmoment ist ein Maß dafür, wie gut ein Querschnittsprofil gegen Biegung widerstehen kann. Es ist eine wichtige Eigenschaft bei der Berechnung von Biegebeanspruchungen in Balken oder Trägern. Je größer das Flächenträgheitsmoment ist, desto widerstandsfähiger ist der Querschnitt gegen Biegung.

Vereinfacht ausgedrückt: Stell dir vor, du hast einen Balken, den du verbiegen möchtest. Das Flächenträgheitsmoment ist wie ein Maß dafür, wie schwer es ist, diesen Balken zu biegen. Wenn das Flächenträgheitsmoment größer ist, ist es schwieriger, den Balken zu biegen, und er wird weniger stark verformt.

In dieser Lerneinheit wollen wir das Flächenträgheitsmoment mittels Integration bestimmen. Wir zeigen wie das Flächenträgheitsmomente mittels Integration ermittelt wird (rechteckiger Querschnitt).

Für ein optimales Verständnis helfen dir drei ausführliche Videoclips und zwei anschauliche Rechenbeispiele zu dem Thema.

Dieser Lerntext ist ein Auszug aus unserem Onlinekurs TM2 – Festigkeitslehre.

Flächenträgheitsmoment – Definition

Das axiale Flächenträgheitsmoment ist ein Maß für den Widerstand eines Querschnitts gegen Biegung. Je größer das Moment ist, desto schwieriger ist es, den betrachteten Körper zu verbiegen.

Zum besseren Verständnis schauen wir uns mal die folgende Grafik an:

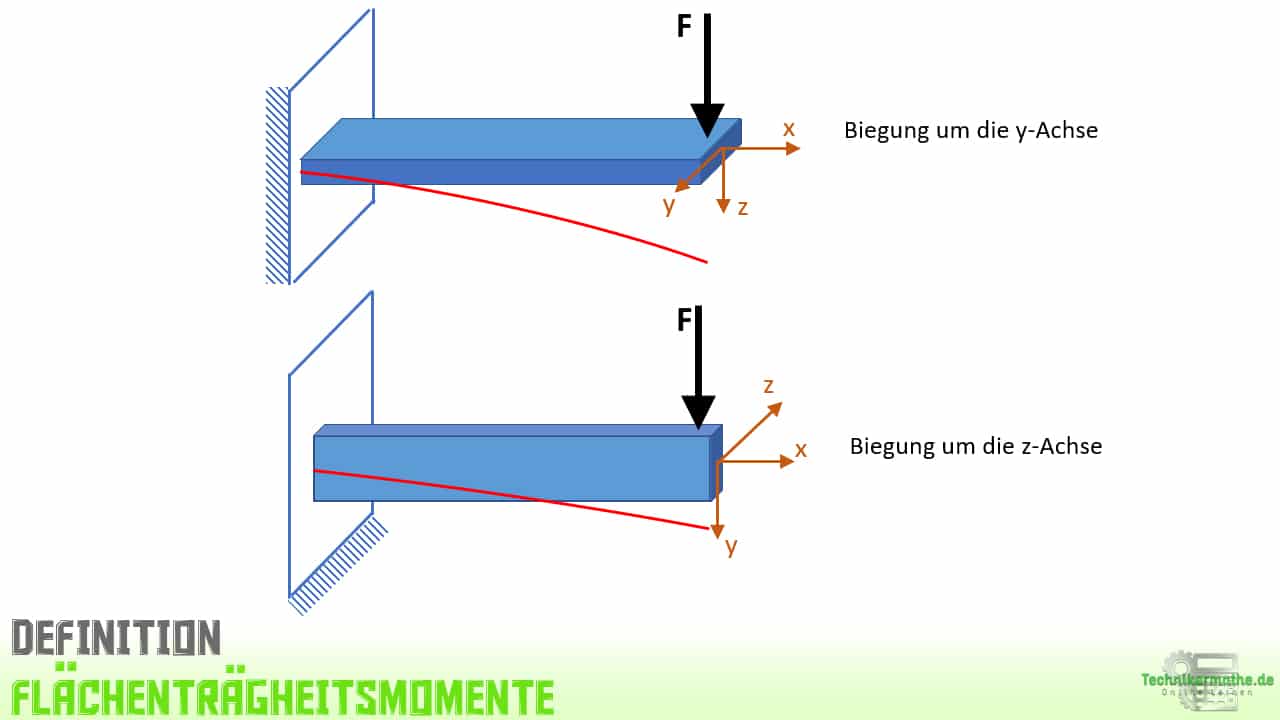
Flächenträgheitsmomente, Definition, Flächenträgheitsmoment, Biegung, Definition, Beispiel — Definition: Flächenträgheitsmoment

In der obigen Grafik ist ein Balken mit einem rechteckigen Querschnitt gegeben. Die y,z-Achsen liegen im Schwerpunkt des Querschnitts.

Betrachten wir zunächst die Biegung um die y-Achse. Damit diese Situation eintritt, müssen äußere Kräfte (bzw. die resultierende äußere Kraft) in Richtung der z-Achse wirken. Ist dies der Fall, so biegt sich der Balken um die y-Achse.

Für die Biegung des Balkens um die z-Achse betrachten wir denselben Balken und stellen ihn uns um 90° gedreht vor, damit wir die Situation grafisch besser darstellen können. Damit nun eine Durchbiegung um die z-Achse resultiert, müssen äußere Kräfte (bzw. die resultierende äußere Kraft) in Richtung der y-Achse wirken.

Wenn wir nun beide Fälle betrachten, so sollte jedem aus der eigenen Erfahrung heraus klar sein, dass der Widerstand bei Biegung um die y-Achse geringer ist, als bei der Biegung des Balkens um die z-Achse.

Damit ist für den obigen Fall das Flächenträgheitsmoment I_y (Widerstand bei Biegung um die y-Achse) kleiner, als das Flächenträgheitsmoment I_z (Widerstand bei Biegung um die z-Achse).

Formeln: Flächenträgheitsmomente

Die beiden Flächenträgheitsmomente I_y und I_z werden auch als Flächenträgheitsmomente 2. Grades oder axiale Flächenträgheitsmomente bezeichnet und können mittels der folgenden Gleichungen berechnet werden:

$I_y = \int z^2 dA$

Flächenträgheitsmoment bezüglich der y-Achse: Maß für den Widerstand gegen Biegung um die y-Achse

$I_z = \int y^2 dA$

Flächenträgheitsmoment bezüglich der z-Achse: Maß für den Widerstand gegen Biegung um die z-Achse

Grundsätzlich werden die obige Gleichungen kaum verwendet, da die Flächenträgheitsmomente in Bezug auf ihre Hauptachsen Tabellenwerken entnommen werden können. Sollen dann Flächenträgheitsmomente für Koordinatenachsen berechnet werden, die nicht im Schwerpunkt liegen, so kann der Satz von Steiner herangezogen werden (siehe spätere Lerneinheit dieser Lektion).

Hauptachsen

Hauptachsen sind Achsen, die im Schwerpunkt der Querschnittsfläche liegen. Eine Symmetrieachse ist auch gleichzeitig eine Hauptachse des Querschnitts. Alle dazu senkrechten Achsen sind ebenfalls Hauptachsen.

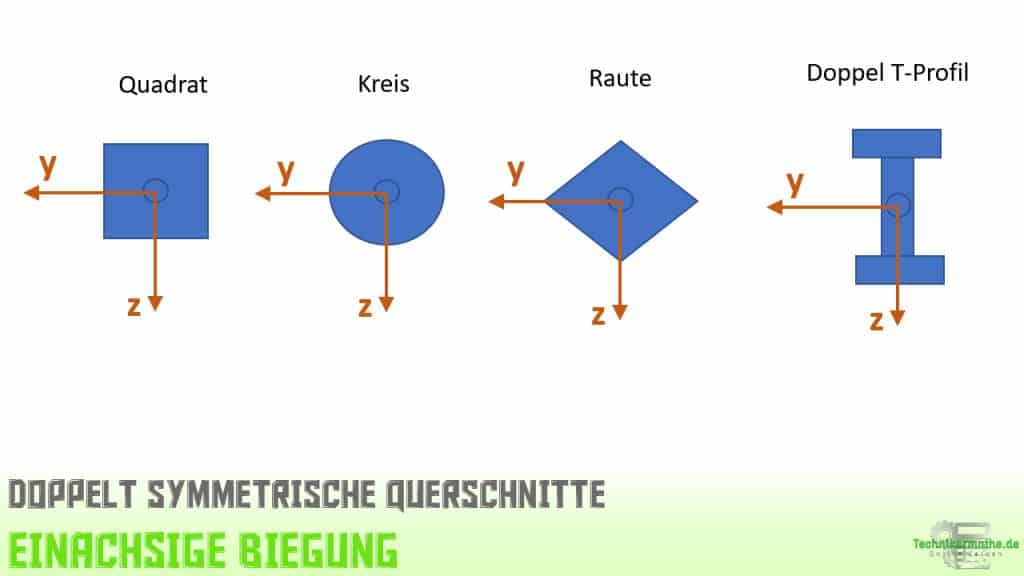
Betrachten wir das y,z-Koordinatensystem eines Querschnitts, so sind bei einem doppelt symmetrischen Querschnitt beide Achsen Hauptachsen.

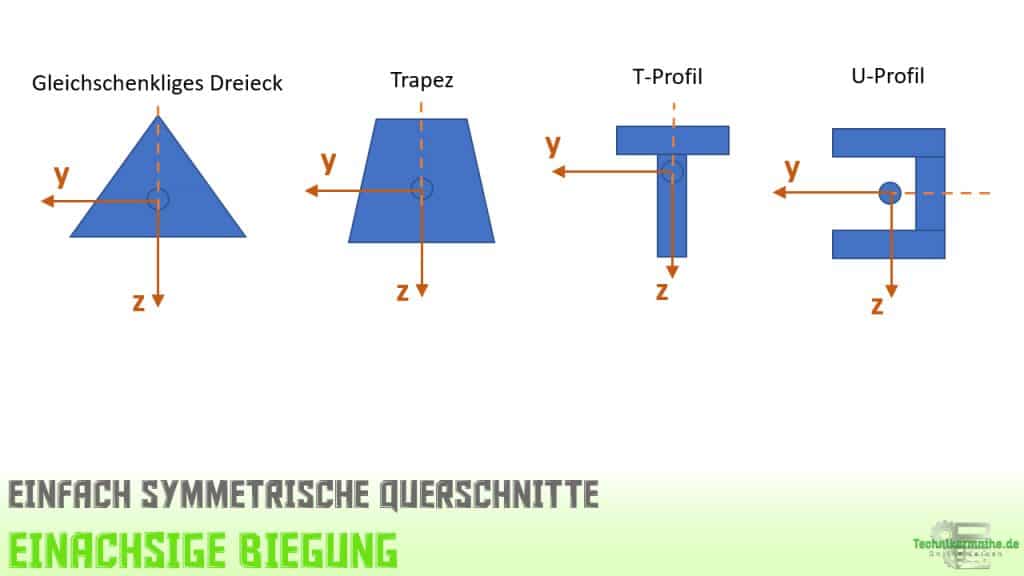
Einfach symmetrische Querschnitte, einfach symmetrisch, symmetrisch, Symmetrieachsen, Hauptachsen, Flächenträgheitsmoment — Einfach symmetrische Profile

Bei einem einfach symmetrischen Querschnitt sind auch beide Achsen Hauptachsen, weil eine Achse die Symmetrieachse ist (=Hauptachse) und die andere Achse zu dieser Symmetrieachse senkrecht steht und damit auch eine Hauptachse darstellt.

Damit sind für die folgenden Berechnungen die beiden y,z-Achsen immer die Hauptachsen des Querschnitts, da wir von einfach und doppelt symmetrischen Querschnitten ausgehen.

Aufgabe: Flächenträgheitsmomente mittels Integration (Rechteck)

Aufgabenstellung

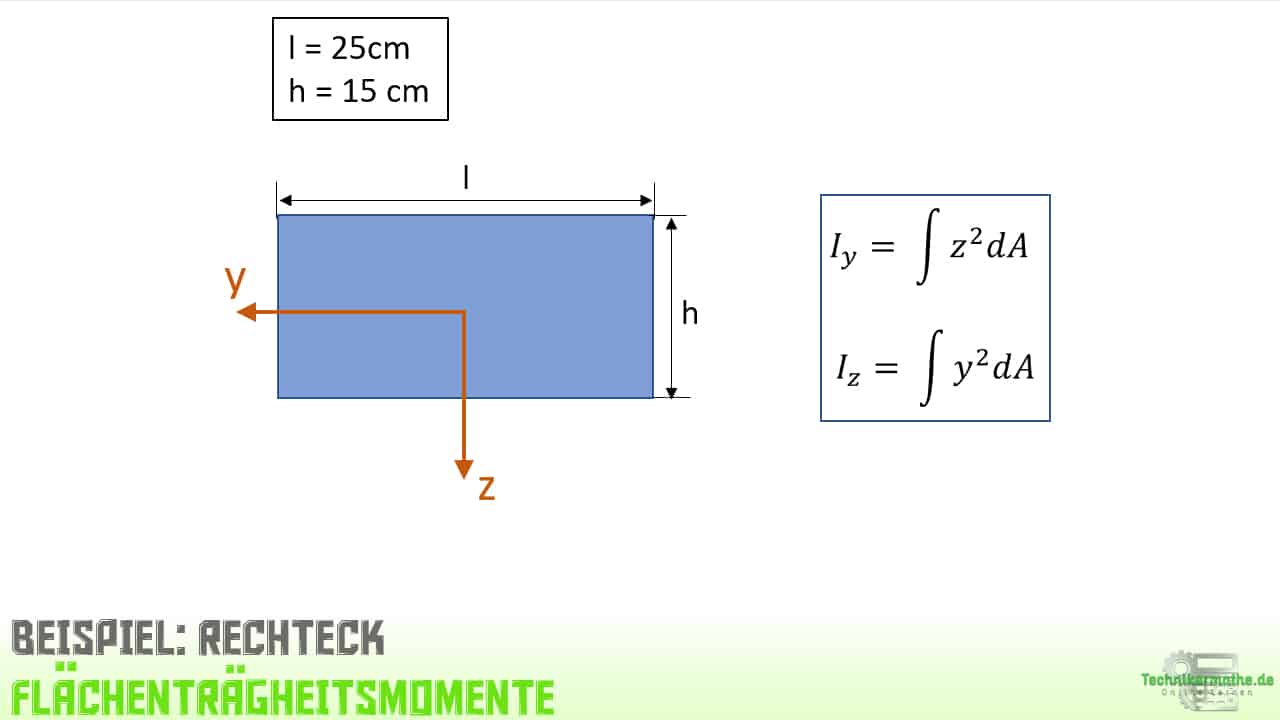
Flächenträgheitsmoment, Beispiel, Berechnung, Integration, Rechteck, rechteckiger Querschnitt — Beispiel: Flächenträgheitsmomente durch Integration

Gegeben sei der obige rechteckige Querschnitt eines Balkens. Es sollen die beiden axialen Flächenträgheitsmomente I_y und I_z berechnet werden und zwar in Bezug auf die beiden angegebenen y,z-Schwerpunktachsen.

Beide Achsen sind Hauptachsen des Querschnitts. Damit können die Flächenträgheitsmomente I_y und I_z ganz einfach aus Tabellenwerken entnommen werden. Wir wollen uns hier aber anschauen, wie diese mittels Integration bestimmt werden.

Lösung im Video

Lösung in Textform

Flächenträgheitsmoment I_y

Zunächst betrachten wir das Flächenträgheitsmoment I_y. Wir wollen also wissen, wie groß der Widerstand gegen Biegung um die y-Achse ist. Bei der Integration gehen wir nun so vor, dass wir einen infinitesimalen (sehr sehr kleinen) Streifen über die Höhe h (in Richtung der z-Achse) laufen lassen. Wir integrieren also über die z-Achse. Dazu müssen wir aber auch die Koordinaten des Rechtecks in Bezug auf die z-Achse genau angeben:

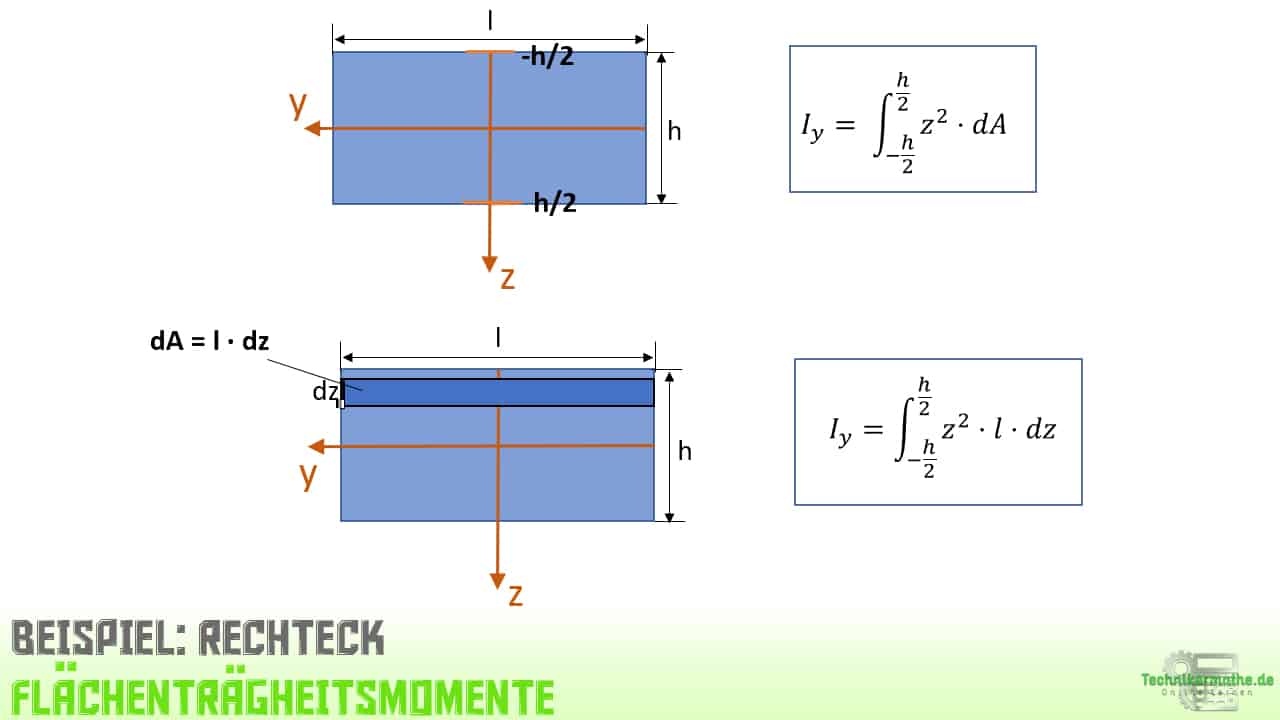
Flächenträgheitsmomente, Beispiel, Berechnung, Integration, Rechteck, Infinitesimaler Streifen — Infinitesimaler Streifen

In der Grafik haben wir zunächst die Koordinaten des Rechtecks in Bezug auf die z-Achse angegeben. Die Achsen greifen im Schwerpunkt der Querschnittsfläche an. Damit ist der Teil oberhalb des Schwerpunkts im negativen z-Bereich und der Teil unterhalb des Schwerpunkts im positiven z-Bereich. Das gesamte Rechteck hat eine Höhe von h. Da der Schwerpunkt eines Rechtecks genau in der Mitte liegt, sind beide Teile h/2 hoch.

Wir können also zunächst die Integralgrenzen angeben:

$I_y = \int_{-h/2}^{h/2} z^2 \cdot dA$

Als nächstes lassen wir einen infinitesimalen Streifen dA über die gesamte Höhe h laufen. In der obigen Gleichung ist $dA$ der Flächeninhalt des infinitesimalen Streifens. Diesen können wir auch ersetzen durch Länge mal Höhe. Die Länge ist in diesem Fall $l$ , die Höhe ist $dz$ :

$dA = l \cdot dz$

Einsetzen:

$I_y = \int_{-h/2}^{h/2} z^2 \cdot l \cdot dz$

Wir haben nun die Gleichung aufgestellt und können mit der Integration beginnen:

$I_y = [ \frac{1}{3} z^3 \cdot l ]_{-h/2}^{h/2}$

Einsetzen der Grenzen:

$I_y = [ \frac{1}{3} (\frac{h}{2})^3 \cdot l - \frac{1}{3} (\frac{-h}{2})^3 \cdot l]$

$I_y = [ \frac{1}{3} \frac{h^3}{8} \cdot l - \frac{1}{3} \frac{-h^3}{8} \cdot l]$

$I_y = [ \frac{1}{24} h^3 \cdot l + \frac{1}{24} h^3 \cdot l]$

$I_y = \frac{h^3 \cdot l}{12}$

Flächenträgheitsmoment I_z

Als nächstes betrachten wir das Flächenträgheitsmoment I_z, wir wollen also das Maß für die Biegung um die z-Achse bestimmen. Bei der Integration gehen wir nun so vor, dass wir einen infinitesimalen (sehr sehr kleinen) Streifen über die Länge l (in Richtung der y-Achse) laufen lassen. Wir integrieren also über die y-Achse. Dazu müssen wir aber auch die Koordinaten des Rechtecks in Bezug auf die y-Achse genau angeben:

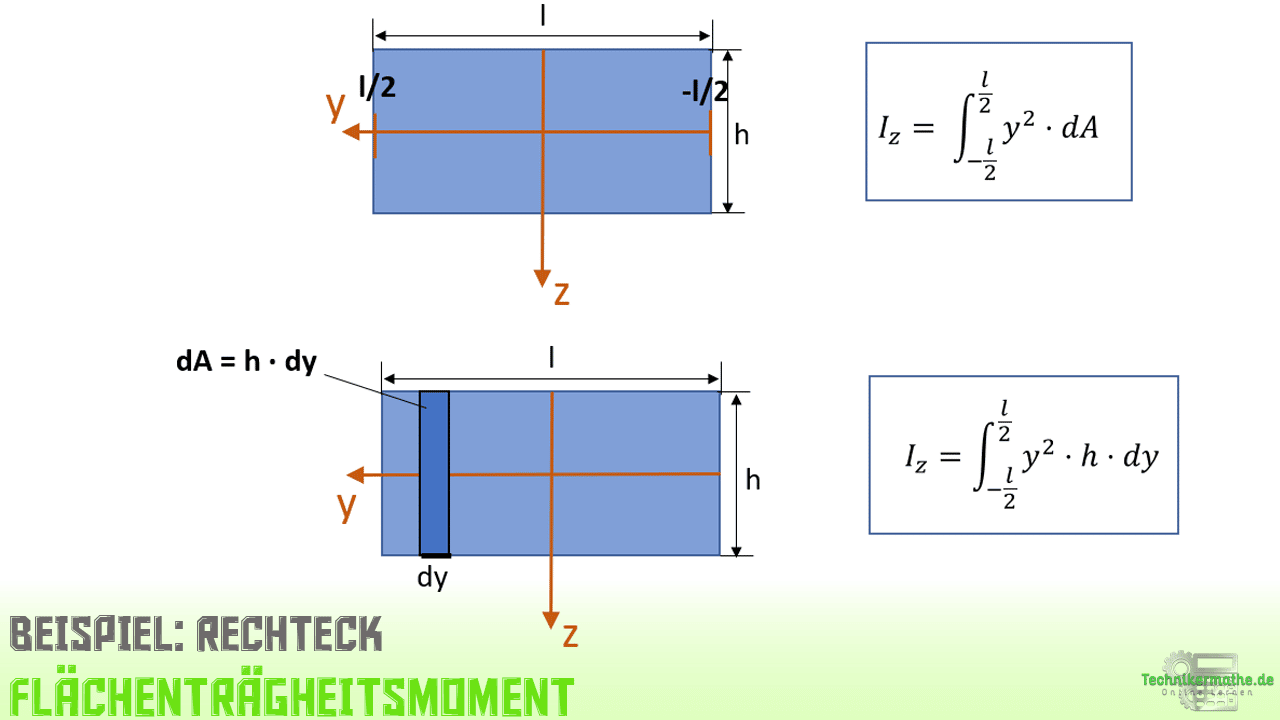
Flächenträgheitsmoment, Beispiel, Rechteck, Integration, Flächenträgheitsmomente, — Infinitesimaler Streifen

In der Grafik haben wir zunächst die Koordinaten des Rechtecks in Bezug auf die y-Achse angegeben. Die Achsen greifen im Schwerpunkt der Querschnittsfläche an. Damit ist der Teil rechts vom Schwerpunkt im negativen y-Bereich und der Teil links vom Schwerpunkt im positiven y-Bereich. Das gesamte Rechteck hat eine Breite von l. Da der Schwerpunkt eines Rechtecks genau in der Mitte liegt, sind beide Teile l/2 groß.

Wir können also zunächst die Integralgrenzen angeben:

$I_z = \int_{-l/2}^{l/2} y^2 \cdot dA$

Als nächstes lassen wir einen infinitesimalen Streifen dA über die gesamte Breite l laufen. In der obigen Gleichung ist $dA$ der Flächeninhalt des infinitesimalen Streifens. Diesen können wir auch ersetzen durch Länge mal Höhe. Die Länge ist in diesem Fall $dy$ , die Höhe ist $h$ :

$dA = h \cdot dy$

Einsetzen:

$I_z = \int_{-l/2}^{l/2} z^2 \cdot h \cdot dy$

Wir haben nun die Gleichung aufgestellt und können mit der Integration beginnen:

$I_z = [ \frac{1}{3} y^3 \cdot h ]_{-l/2}^{l/2}$

Einsetzen der Grenzen:

$I_z = [ \frac{1}{3} (\frac{l}{2})^3 \cdot h - \frac{1}{3} (\frac{-l}{2})^3 \cdot h]$

$I_z = [ \frac{1}{3} \frac{l^3}{8} \cdot h - \frac{1}{3} \frac{-l^3}{8} \cdot h]$

$I_z = [ \frac{1}{24} l^3 \cdot h + \frac{1}{24} l^3 \cdot h]$

$I_z = \frac{l^3 \cdot h}{12}$

Was gibt es noch bei uns?

Optimaler Lernerfolg durch tausende Übungsaufgaben

Quizfrage 1

“Wusstest du, dass unter jedem Kursabschnitt eine Vielzahl von verschiedenen interaktiven Übungsaufgaben bereitsteht, mit denen du deinen aktuellen Wissensstand überprüfen kannst?”

Alle Technikerschulen im Überblick

Zum Verzeichnis der Technikerschulen (Alles Rund um die Schulen) — Zum Verzeichnis der Technikerschulen

Kennst du eigentlich schon unser großes Technikerschulen-Verzeichnis für alle Bundesländer mit allen wichtigen Informationen (Studiengänge, Kosten, Anschrift, Routenplaner, Social-Media) ? Nein? – Dann schau einfach mal hinein:

Was ist Technikermathe?

Unser Dozent Jan erklärt es dir in nur 2 Minuten!

Oder direkt den > kostenlosen Probekurs < durchstöbern? – Hier findest du Auszüge aus Alle Onlinekurse Technikermathe!

Geballtes Wissen in derzeit 26 Kursen

Hat dir dieses Thema gefallen? – Ja? – Dann schaue dir auch gleich die anderen Themen zu den Kursen

WT3 (Werkstoffprüfung) und
TM1 (Technische Mechanik – Statik) an.

Lerne nun erfolgreich mit unserem Onlinekurs Technische Mechanik 1 — TM1 (Technische Mechanik)

Lerne nun erfolgreich mit unserem Onlinekurs Werkstofftechnik 3 — WT3 (Werkstoffprüfung)

Perfekte Prüfungsvorbereitung für nur 14,90 EUR/Jahr pro Kurs

++ Günstiger geht’s nicht!! ++

Oder direkt Mitglied werden und Alle unsere Onlinekurse (inkl. Webinare + Unterlagen) sichern ab 7,40 EUR/Monat ++ Besser geht’s nicht!! ++