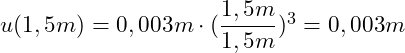TM2 – Konstante und örtliche Dehnung im Stab [Formeln, Beispiele, Berechnung]

Dehnungen im Stab beziehen sich auf die Verlängerung des Stabes entlang seiner Längsrichtung, wenn er einer Zugkraft ausgesetzt ist. Wenn du zum Beispiel an beiden Enden eines Stabes ziehst, wird er sich in Richtung der Zugkraft dehnen. Die Dehnung wird oft als Verhältnis der Verlängerung zur ursprünglichen Länge des Stabes ausgedrückt und kann in Prozent oder als Bruchteil angegeben werden.

Dehnung im Stab ist ein wichtiges Konzept in der Festigkeitslehre und wird verwendet, um die Belastung und Verformung von Materialien unter Zugkraft zu analysieren.

In diesem Kursabschnitt befassen wir uns mit Dehnungen im Stab. Dehnungen im Stab können auf unterschiedliche Weise wirken.

Für ein optimales Verständnis helfen dir drei ausführliche Videoclips und zwei anschauliche Rechenbeispiele zu dem Thema.

Dieser Lerntext ist ein Auszug aus unserem Onlinekurs TM2 – Festigkeitslehre.

Konstante Dehnung

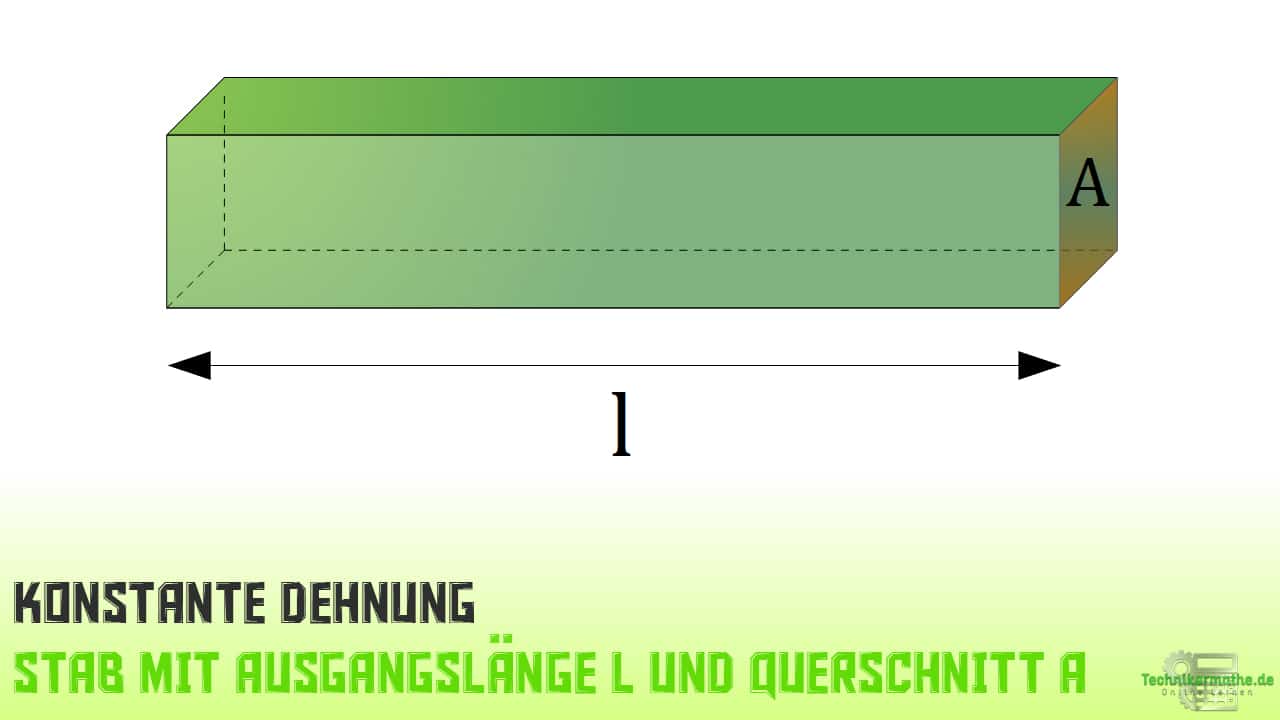
Wir wollen zunächst die konstante Dehnung betrachten, d.h. die Dehnung ist im gesamten Stab gleich. Dazu betrachten wir einen elastischen Stab der Länge l mit konstantem Querschnitt A:

Bringen wir nun eine Zugkraft an den Stab an, so verlängert sich dieser um $\triangle l$ :

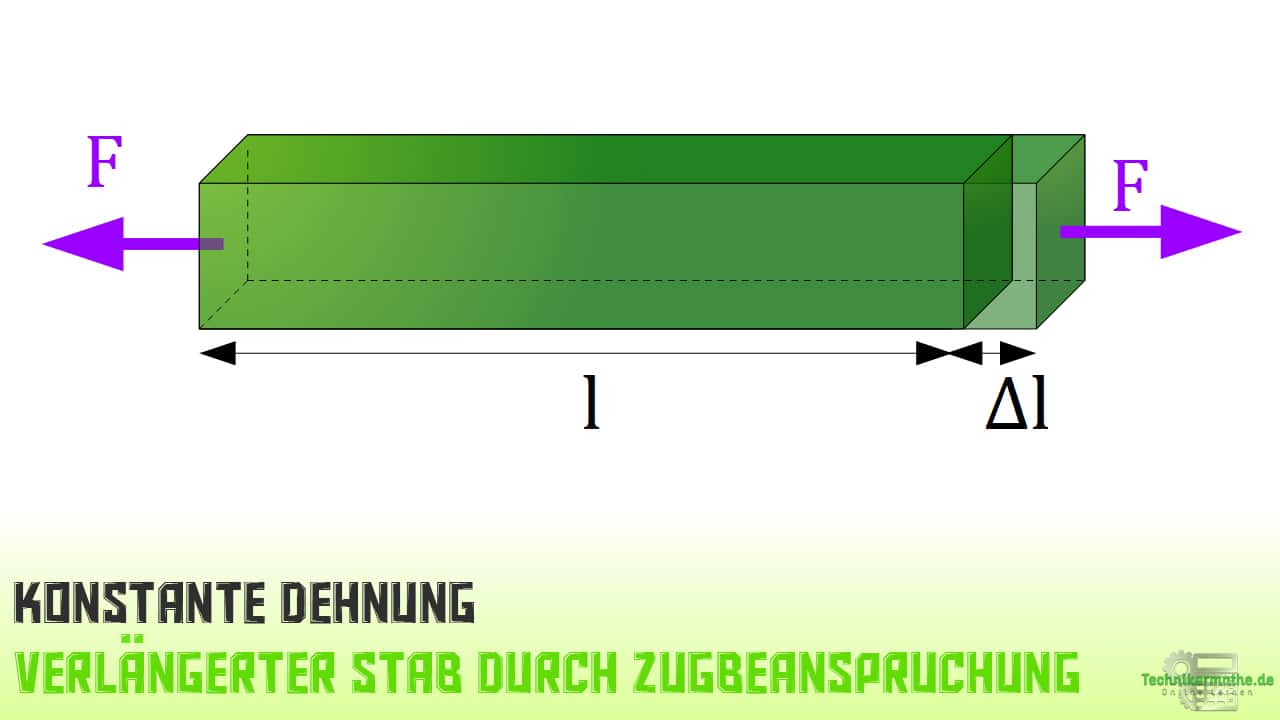
Dehnungen im Stab, konstante Dehnung, Zugkraft, Zugstab, Dehnung — Zugkraft: Konstante Dehnung

Als Dehnung wird dabei das Verhältnis zwischen der Längenänderung $\triangle l$ und der Ausgangslänge $l$ beschrieben:

Dehnung im Stab

$\epsilon = \dfrac{\triangle l}{l}$

mit

$l$ Ausgangslänge des Stabs

$\triangle l$ Längenänderung

Merk’s dir!

Die Dehnung ist eine dimensionslose Größe. Verlängert sich der Stab, so wird die Längenänderung $\triangle l$ positiv berücksichtigt, bei einer Verkürzung wird die Längenänderung negativ berücksichtigt.

Einführungsbeispiel: Dehnung im Stab

Gegeben sei ein Stab mit eine Länge von l = 2 m. Der Stab verkürzt sich aufgrund von Druckkräften um 0,02m.

Wie groß ist die Dehnung im Stab?

$\epsilon = \dfrac{-0,02m}{2m} = -0,01$ .

Die Dehnung im Stab beträgt infolge der Druckkräfte -1%. Damit zieht sich der Stab um 1% zusammen.

Die obige Gleichung gilt nur, wenn die Dehnung im Stab über die gesamte Stabachse konstant bleibt. Ist die Dehnung nicht im gesamten Stab konstant, so spricht man von einer örtlichen Dehnung.

Örtliche Dehnung

Ist eine örtliche Dehnung gegeben, so ist die Dehnung nicht mehr im gesamten Stab konstant. Wir müssen dann ein Stabelement betrachten, um die Gleichung für die örtliche Dehnung herzuleiten.

In der obigen Grafik ist ein Stab der Länge l gegeben. Wir betrachten zunächst ein infinitesimal kleines Element des Stabes im unbelasteten Zustand mit der Länge dx. Die linke Querschnittsfläche ist also mit Position $x$ gegeben, die rechte Querschnittsfläche mit der Position $x + dx$ .

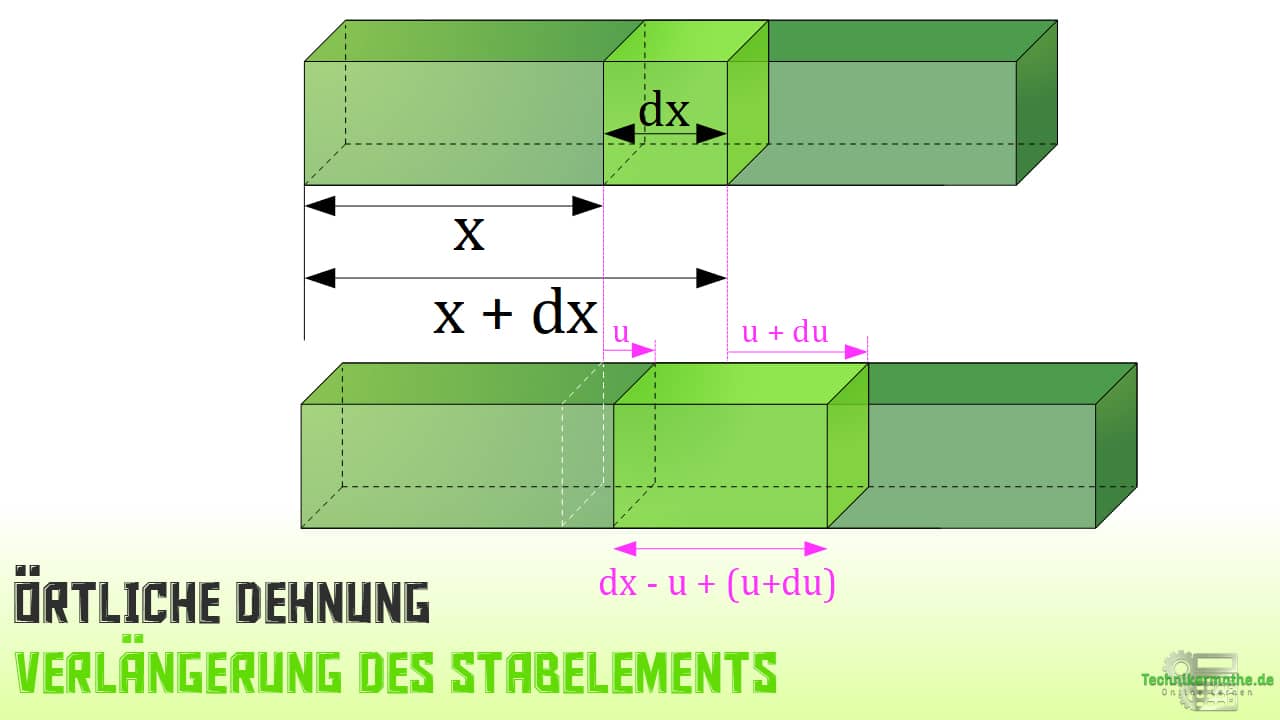
örtliche Dehnung, Dehnung im Stab, Dehnung, Längenänderung, Verlängerung, Stab — Dehnungen im Stab: Örtliche Dehnung

Wir betrachten im nächsten Schritt eine Verlängerung des Stabes z.B. durch eine Zugkraft. Damit verschieben sich die Querschnittsflächen am linken und rechten Rand des Stabelements. Die Verschiebung des linken Querschnitts bezeichnen wir mit $u$ , die Verschiebung am rechten Querschnitt mit $u + du$ .

Wir können aus diesen Angaben nun die Länge des Stabelements berechnen:

$dx - u + (u + du) = dx - u + u + du = dx + du$

Die neue Länge des Stabelements beträgt also $dx + du$ . Hierbei ist $dx$ die Ausgangslänge und damit $du$ die Längenänderung.

Die Dehnung ist allgemein der Quotient aus Längenänderung $du$ und Ausgangslänge $dx$ :

Örtliche Dehnung

$\epsilon(x) = \dfrac{du}{dx}$

Ist die Verschiebung $u(x)$ gegeben, so können wir durch Differenzieren (Ableiten) der Funktion nach x die örtliche Dehnung $\epsilon (x)$ berechnen:

$\epsilon (x) = \dfrac{du}{dx}} = u'(x)$

Ist die örtliche Dehnung $\epsilon(x)$ gegeben, so kannst du die Verschiebung u(x) aus der obigen Gleichung bestimmen. Dazu löst du diese zunächst nach $du$ auf:

$du = \epsilon(x) dx$

Danach kannst du durch die Integration die Verschiebung u(x) bestimmen:

$\int_0^l du = \int_0^l \epsilon(x) \; dx$

$u(l) - u(0) = \int_0^l \epsilon(x) \; dx$

Hierbei ist u(l) – u(0) nichts anderes als die Änderung der Länge des Stabes:

Längenänderung bei örtlicher Dehnung

$\triangle l = \int_0^l \epsilon(x) \; dx$

Beispiel 1: Längenänderung berechnen

Aufgabenstellung

Gegeben sei ein Stab mit der Länge l = 1,2m, welcher infolge einer Zugkraft verlängert wird. Die dadurch resultierende Dehnung sei linear und gegeben mit:

$\epsilon(x) = 0,005 \cdot \dfrac{x}{l}$

Bestimme die Längenänderung!

Zur Berechnung der Änderung der Länge wenden wir die folgende Gleichung an:

$\triangle l = \int_0^l \epsilon(x) \; dx$

Wir setzen als nächstes die örtliche Dehnung ein:

$\triangle l = \int_0^l 0,005 \cdot \dfrac{x}{l} \; dx$

Als nächstes führen wir die Integration durch:

$\triangle l = \int_0^l 0,005 \cdot \dfrac{x}{l} \; dx$

Konstanten vor das Integral ziehen:

$\triangle l = \dfrac{0,005}{l} \int_0^l x \; dx$

Integration durchführen:

$\triangle l = \dfrac{0,005}{l} [\dfrac{1}{2} x^2 ]_0^l$

$\triangle l = \dfrac{0,005}{l} [\dfrac{1}{2} l^2 - \dfrac{1}{2} 0^2 ]$

$\triangle l = \dfrac{0,005}{l} \dfrac{1}{2} l^2$

$\triangle l = 0,0025 l$

Die Ausgangslänge beträgt l = 1,2m:

$\triangle l = 0,0025 \cdot 1,2m = 0,003m$

Die Längenänderung ist gegeben mit 0,003 Meter. Damit Verlängert sich der Stab um 0,003 Meter auf 1,203 Meter.

Beispiel 2: Örtliche Dehnung berechnen

Aufgabenstellung

Gegeben sei ein Stab der Länge l. Die Verschiebung, also die Änderung der Länge sei gegeben mit der folgenden Funktion:

$u(x) = u_0 \cdot (\dfrac{x}{l})^3$

Gegeben seien außerdem die folgenden Zahlenwerte:

$u_0 = 0,003m , l = 1,5m$

1.Bestimme die Längenänderung Δl!

2.Wie groß ist die Dehnung an den Stelllen x/l = 0,4 und x/l = 0,8?

Längenänderung bestimmen

Zunächst bestimmen wir die Längenänderung wie folgt:

$\triangle l = u(l) - u(0)$

Wir setzen also zunächst x = l = 1,5m und dann x = 0 und ziehen die beiden Ergebnisse voneinander ab:

$u(1,5m) = 0,003m \cdot (\dfrac{1,5m}{1,5m})^3 = 0,003m$

$u(0) = 0,003m \cdot (\dfrac{0}{1,5m})^3 = 0$

Es ergibt sich damit eine Längenänderung von:

$\triangle l = 0,003m - 0 = 0,003m$

Dehnung bestimmen

Im nächsten Schritt bestimmen die Dehnung $\epsilon(x)$ . Dazu müssen wir zunächst die Dehnung mittels der folgenden Gleichung bestimmen:

$\epsilon (x) = u'(x)$

Wir leiten also die Verschiebungsfunktion u(x) ab und erhalten damit den Dehnungsverlauf:

$\epsilon(x) = u'(x) = 3 \cdot u_0 \cdot (\dfrac{x}{l})^2$

Nachdem wir den Dehnungsverlauf allgemein bestimmt haben, wollen wir als nächstes die Dehnung an den Stellen x/l = 0,5 und x/l = 1 bestimmen:

$\epsilon(x) = 0,009m \cdot (0,5)^2 = 0,00225$

$\epsilon(x) = 0,009m \cdot (0,5)^2 = 0,009$

Die Dehnung an der Stelle x/l = 0,5 (genau mittig) beträgt 0,225% und an der Stelle x/l = 1 (am rechten Rand) beträgt 0,9%.

Was kommt als Nächstes?

Nachdem du jetzt alles zu Dehnungen im Stab weißt, behandeln wir in der folgenden Lektion den Zugversuch, das Spannungs-Dehnungs-Diagramm sowie die Hookesche Gerade.

Was gibt es noch bei uns?

Optimaler Lernerfolg durch tausende Übungsaufgaben

Quizfrage 1

“Wusstest du, dass unter jedem Kursabschnitt eine Vielzahl von verschiedenen interaktiven Übungsaufgaben bereitsteht, mit denen du deinen aktuellen Wissensstand überprüfen kannst?”

Alle Technikerschulen im Überblick

Zum Verzeichnis der Technikerschulen (Alles Rund um die Schulen) — Zum Verzeichnis der Technikerschulen

Kennst du eigentlich schon unser großes Technikerschulen-Verzeichnis für alle Bundesländer mit allen wichtigen Informationen (Studiengänge, Kosten, Anschrift, Routenplaner, Social-Media) ? Nein? – Dann schau einfach mal hinein:

Was ist Technikermathe?

Unser Dozent Jan erklärt es dir in nur 2 Minuten!

Oder direkt den > kostenlosen Probekurs < durchstöbern? – Hier findest du Auszüge aus Alle Onlinekurse Technikermathe!

Geballtes Wissen in derzeit 26 Kursen

Hat dir dieses Thema gefallen? – Ja? – Dann schaue dir auch gleich die anderen Themen zu den Kursen

WT3 (Werkstoffprüfung) und
TM1 (Technische Mechanik – Statik) an.

Lerne nun erfolgreich mit unserem Onlinekurs Technische Mechanik 1 — TM1 (Technische Mechanik)

Lerne nun erfolgreich mit unserem Onlinekurs Werkstofftechnik 3 — WT3 (Werkstoffprüfung)

Perfekte Prüfungsvorbereitung für nur 14,90 EUR/Jahr pro Kurs

++ Günstiger geht’s nicht!! ++

Oder direkt Mitglied werden und Alle unsere Onlinekurse (inkl. Webinare + Unterlagen) sichern ab 7,40 EUR/Monat ++ Besser geht’s nicht!! ++