TM2 – Biegelinie und Verdrehung (Neigungswinkel) aus Tabelle [Erklärung, Beispiel, Berechnung]

Wir betrachten in dieser Lerneinheit eine Aufgabe zur Berechnung der Biegelinie und der Verdrehung (Angabe des Neigungswinkels) anhand einer Tabelle.

Der Neigungswinkel bei der Durchbiegung von Balken gibt die Neigung der Balkenachse in der Einheit Radiant oder Grad an. Es ist also nichts anderes als der Winkel von der ursprünglichen Lage der Balkenachse hin zur gebogenen Balkenachse, die durch äußere Kräfte oder Momente hervorgerufen wird.

In diesem Kursabschnitt befassen wir uns mit der Bestimmung der Biegelinie und Verdrehung an den Auflagern.

Für ein optimales Verständnis helfen dir drei ausführliche Videoclips und zwei anschauliche Rechenbeispiele zu dem Thema.

Dieser Lerntext ist ein Auszug aus unserem Onlinekurs TM2 – Festigkeitslehre.

In dieser Aufgabe wollen wir die Biegelinie und die Verdrehung (=Neigungswinkel) an den Auflagern bestimmen. Wir werden dazu die Tabelle: Übersicht der Biegelinien heranziehen (die gesamte Tabelle findest du im Kapitel TM2-13-9, wir zeigen hier die relevanten Ausschnitte). Das hat den Vorteil, dass wir die Biegelinie nicht mehr durch Integration bestimmen müssen. Es entfällt ebenfalls die Bestimmung der Lagerkräfte sowie die Bestimmung des Momentenverlaufs.

Merk’s dir!

Habt ihr eine Aufgabe gegeben, so gleicht sie mit der Tabelle: Übersicht der Biegelinien ab. Es gibt außerdem noch weitere Übersichten im Internet, in denen ihr Biegelinien für unterschiedliche Balkenbelastungen und Lagerungen findet. Findet ihr eure Aufgabe dort wieder, so könnt ihr die Biegelinie einfach ablesen und die gegebenen Werte einsetzen. Das erspart euch eine Menge an Arbeit.

Andernfalls müsst ihr den bereits bekannten Weg gehen:

Lagerkräfte bestimmen
Momentenverlauf /-verläufe bestimmen
Biegelinie/n durch Integration bestimmen
Integrationskonstanten über die Rand-und Übergangsbedingungen ermitteln

Wir betrachten nun eine Aufgabe in welcher wir die Biegelinie aus der Tabelle ablesen können.

Beispiel : Biegelinie und Verdrehung

Aufgabenstellung

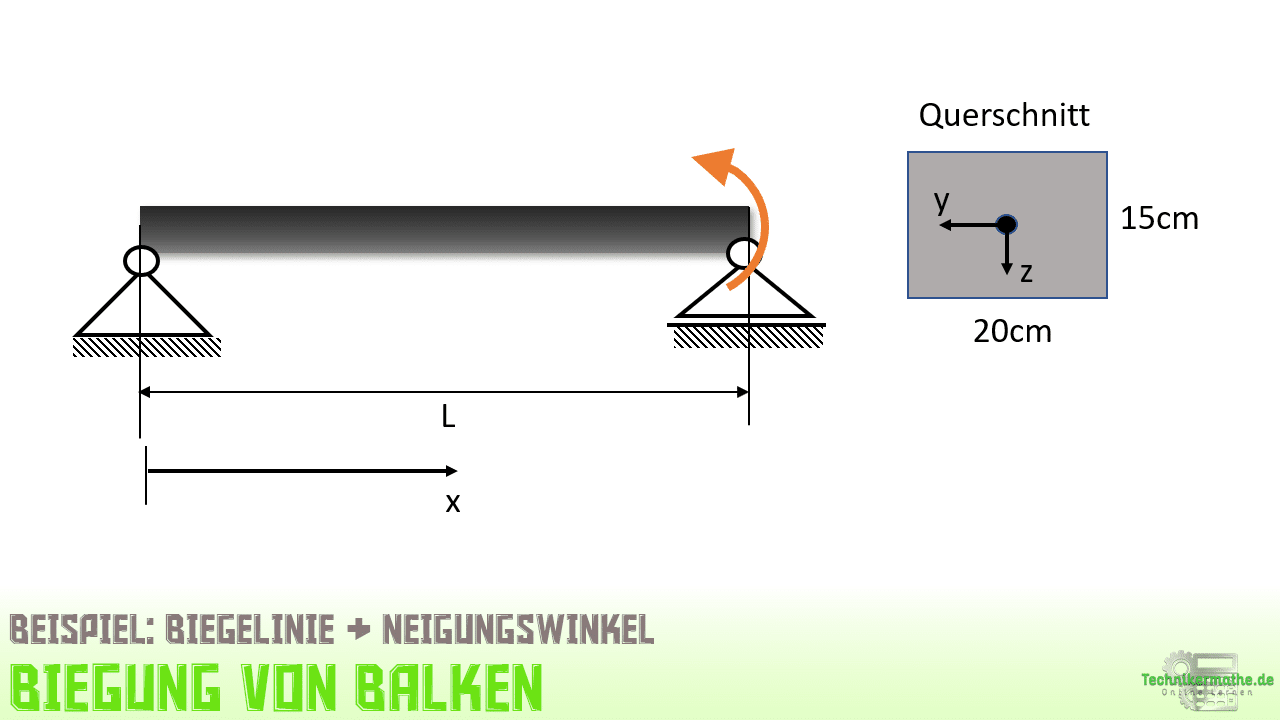
Biegelinie, Neigungswinkel, Beispiel, Verdrehung, Biegelinie und Verdrehung, Tabelle, Randbedingungen, Auflager — Beispiel: Biegelinie und Verdrehung am Balken

Gegeben sei der obige Balken, welcher auf einem Festlager und einem Loslager gelagert ist. Der Balken wird durch ein Moment M = 180 Nm belastet. Folgende weiter Daten sind gegeben:

$L = 3,5m$

$E = 210.000 \frac{N}{mm^2}$

a) Bestimme die Biegelinie im gesamten Balken!

b) Bestimme die Durchbiegung bei x = 1m und bei x = 2m!

c) Bestimme die Neigungswinkel an den Auflagern!

Lösung a) Biegelinie bestimmen

Wir sollen die Biegelinie im gesamten Balken bestimmen. Zunächst schauen wir uns den gegebenen Balken inklusive Lagerung und Belastung in der Übersicht der Biegelinien an und sehen, dass dieser Fall dort vertreten ist:

Biegelinie, Verdrehung, Moment, Einspannung, Balken, Tabelle, Biegelinie und Verdrehung, Beispiel — Tabellenausschnitt: Übersicht der Biegelinien

Wir können für den gegebenen Balken die Biegelinie ablesen:

$w = \dfrac{M \cdot x}{6 \cdot EI \cdot L} \cdot (L^2 - x^2)$

Wir müssen als nächstes die gegebenen Werte einsetzen:

$M = 180 Nm$

$L = 3,5m$

$E = 210.000 \frac{N}{mm^2} = 2,1 \cdot 10^{11} \frac{N}{m^2}$

Es fehlt noch das Flächenträgheitsmoment I, da nicht die Biegesteifigkeit sondern der Elastizitätsmodul E gegeben ist. Das Flächenträgheitsmoment können wir über die Querschnittsfläche bestimmen. Es ist eine rechteckige Querschnittsfläche gegeben, damit ergibt sich das Flächenträgheitsmoment zu (siehe Lektion 11):

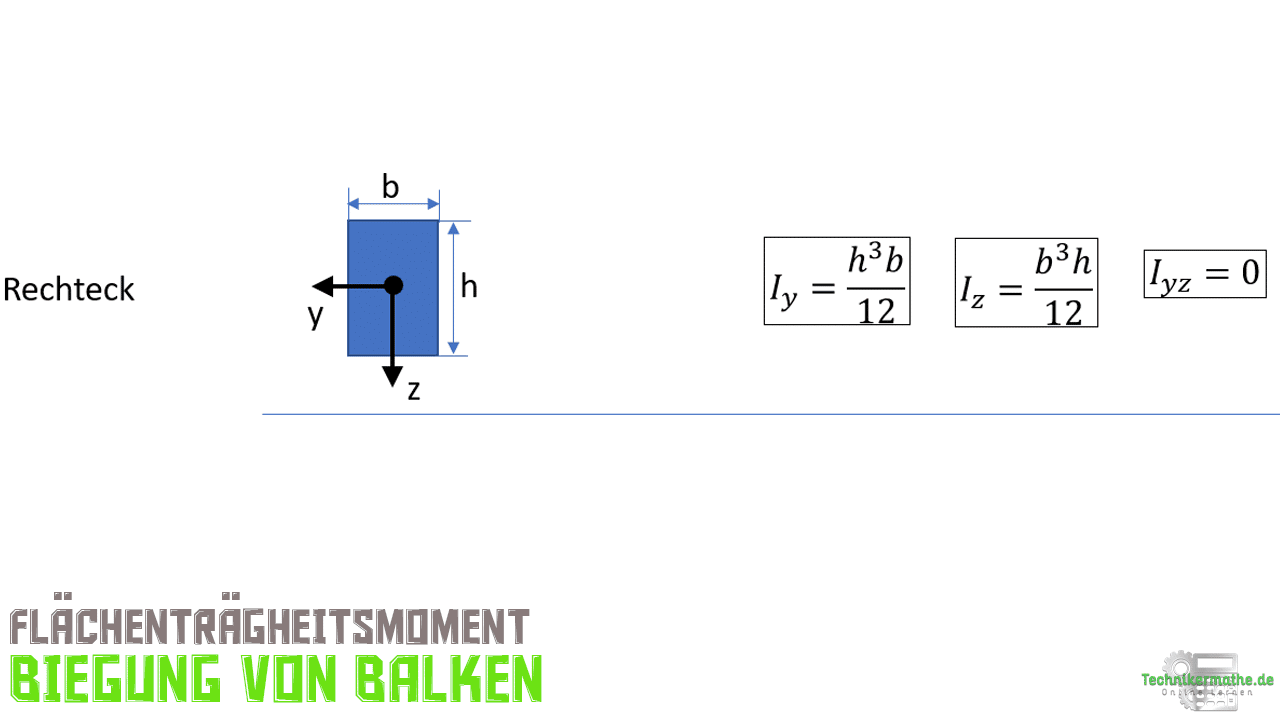
Biegung, Balken, Flächenträgheitsmoment, Biegelinie, Tabelle, Verdrehung, Balken, Rechteck — Flächenträgheitsmoment eines Rechtecks

Wir suchen hier das Flächenträgheitsmoment in Bezug auf die y-Achse:

$I_y = \dfrac{h^3 \cdot b}{12}$

In der Aufgabenstellung haben wir die folgenden Werte gegeben:

$h = 15cm$

$b = 20cm$

Einsetzen der Werte in die Formel für das Flächenträgheitsmoment ergibt:

$I_y = \dfrac{(15cm)^3 \cdot 20cm}{12}$

$I_y = 5.625 cm^4$

Wir rechnen das ganze noch in m⁴ um:

$I_y = 5.625 : 100^4 = 0,00005625 m^4$

Wir können als nächstes die Biegesteifigkeit berechnen:

$EI = E \cdot I = 2,1 \cdot 10^{11} \frac{N}{m^2} \cdot 0,00005625 m^4 = 11.812.500 Nm^2$

Nachdem wir alle Werte gegeben haben, können wir die Biegelinie bestimmen:

$w = \dfrac{180 Nm \cdot x}{6 \cdot 11.812.500 Nm^2 \cdot 3,5m} \cdot ((3,5m)^2 - x^2)$

$w = 0,000000726 \frac{1}{m^2} \cdot x (12,25m^2 - x^2)$

Wir haben die Biegelinie bestimmt.

Lösung b) Durchbiegung

Als nächstes suchen wir die Durchbiegung des Balkens an den Stellen x = 1m und x = 2m. Dazu setzen wir diese Werte in die Biegelinie ein.

x = 1m:

$w = 0,000000726 \frac{1}{m^2} \cdot 1m \cdot (12,25m^2 - (1m)^2)$

$w = 0,0000089m = 0,0089 mm$

x = 2m:

$w = 0,000000726 \frac{1}{m^2} \cdot 2m \cdot (12,25m^2 - (2m)^2)$

$w = 0,000071 m = 0,071 mm$

Die Durchbiegung bei x=2m ist größer als die Durchbiegung bei x = 1m. Die Durchbiegungen sind positiv, d.h. der Balken verbiegt sich vertikal nach unten in positive z-Richtung.

Lösung c) Neigungswinkel

Wir wollen als letztes die Neigung des Balkenquerschnitts φ an den Auflagern bestimmen. Dazu können wir ebenfalls die Tabelle: Übersicht der Biegelinie heranziehen. Sollte diese Information nicht gegeben sein, so müssen wir die Biegelinie ableiten, denn es gilt Folgendes:

$w' = - \varphi$

Wir zeigen hier beide Varianten.

Variante 1: Berechnung des Neigungswinkels

Zunächst leiten wir die Biegelinie ab:

$w = 0,000000726 \frac{1}{m^2} \cdot x (12,25m^2 - x^2)$

$w = 0,000000726 \frac{1}{m^2} \cdot 12,25m^2 \cdot x - 0,000000726 \frac{1}{m^2} \cdot x^3$

$w' = 0,000000726 \frac{1}{m^2} \cdot 12,25m^2 - 3 \cdot 0,000000726 \frac{1}{m^2} \cdot x^2$

Danach setzen wir w’ = -φ:

$w' = -\varphi = 0,000000726 \frac{1}{m^2} \cdot 12,25m^2 - 3 \cdot 0,000000726 \frac{1}{m^2} \cdot x^2$

$\varphi = - [0,000000726 \frac{1}{m^2} \cdot 12,25m^2 - 3 \cdot 0,000000726 \frac{1}{m^2} \cdot x^2]$

$\varphi = -0,000000726 \frac{1}{m^2} \cdot 12,25m^2 + 3 \cdot 0,000000726 \frac{1}{m^2} \cdot x^2$

Wir suchen die Verdrehung der Balkenenden, also die Verdrehung des Balkens an den Auflagern bei x = 0 (Festlager) und x = L = 3,5m (Loslager).

Festlager bei x = 0:

$\varphi(0)= -0,000000726 \frac{1}{m^2} \cdot 12,25m^2 + 3 \cdot 0,000000726 \frac{1}{m^2} \cdot 0^2$

$\varphi(0) = -0,0000089 rad$

Der Winkel resultiert in Radiant. Da der Winkel negativ resultiert, erfolgt die Drehung des Balkens am Festlager bei x = 0 in einer Rechtsdrehung.

Loslager bei x = L = 3,5m:

$\varphi(3,5)= -0,000000726 \frac{1}{m^2} \cdot 12,25m^2 + 3 \cdot 0,000000726 \frac{1}{m^2} \cdot (3,5m)^2$

$\varphi(3,5) = 0,0000178 rad$

Der Winkel resultiert in Radiant. Da der Winkel positiv resultiert, erfolgt die Drehung des Balkens am Loslager bei x = L in einer Linksdrehung.

Variante 2: Neigungswinkel aus Tabelle

In der Grafik weiter oben ist neben der Biegelinie auch die Verdrehung an den Auflagern angegeben:

$\varphi(0) = -\dfrac{M \cdot L}{6 \cdot EI}$

$\varphi(L) = \dfrac{M \cdot L}{3 \cdot EI}$

Einsetzen der gegebenen Werte:

$\varphi(0) = -\dfrac{180Nm \cdot 3,5m}{6 \cdot 11.812.500 Nm^2}$

$\varphi(0) = -0,0000089 rad$

$\varphi(L) = \dfrac{180Nm \cdot 3,5m}{3 \cdot 11.812.500 Nm^2}$

$\varphi(L) = 0,0000178 rad$

Wir können zum Schluss den gegebenen Winkel von Radiant in Grad umrechnen:

$\varphi(0)_{Grad} = \dfrac{-0,0000089 rad \cdot 180^\circ}{\pi}$

$\varphi(0)_{Grad} = -0,00051^\circ$

$\varphi(L)_{Grad} = \dfrac{0,0000178 rad \cdot 180^\circ}{\pi}$

$\varphi(L)_{Grad} = 0,001^\circ$

Biegelinie, Verdrehung, Beispiel, Durchbiegung, Neigungswinkel, Neigung, Tabelle — Balken mit Durchbiegung und Neigungswinkeln

In der obigen Grafik siehst du den Balken sowie seine Durchbiegung nach unten und die Verdrehungen (Winkel) an den Auflagern [Hinweis: Die Durchbiegung und die Verdrehung sind in der Grafik viel größer eingezeichnet, damit Durchbiegung und Verdrehung klar erkennbar gemacht werden können. In der Realität zeigen die Ergebnisse, dass die Durchbiegung und die Verdrehung infinitesimal klein sind].

Was gibt es noch bei uns?

Optimaler Lernerfolg durch tausende Übungsaufgaben

Übungsbereich (Demo) - Lerne mit mehr als 4000 Übungsaufgaben für deine Prüfungen

Quizfrage 1

“Wusstest du, dass unter jedem Kursabschnitt eine Vielzahl von verschiedenen interaktiven Übungsaufgaben bereitsteht, mit denen du deinen aktuellen Wissensstand überprüfen kannst?”

Alle Technikerschulen im Überblick

Zum Verzeichnis der Technikerschulen (Alles Rund um die Schulen) — Zum Verzeichnis der Technikerschulen

Kennst du eigentlich schon unser großes Technikerschulen-Verzeichnis für alle Bundesländer mit allen wichtigen Informationen (Studiengänge, Kosten, Anschrift, Routenplaner, Social-Media) ? Nein? – Dann schau einfach mal hinein:

Was ist Technikermathe?

Unser Dozent Jan erklärt es dir in nur 2 Minuten!

Oder direkt den > kostenlosen Probekurs < durchstöbern? – Hier findest du Auszüge aus Alle Onlinekurse Technikermathe!

Geballtes Wissen in derzeit 26 Kursen

Hat dir dieses Thema gefallen? – Ja? – Dann schaue dir auch gleich die anderen Themen zu den Kursen

WT3 (Werkstoffprüfung) und
TM1 (Technische Mechanik – Statik) an.

Lerne nun erfolgreich mit unserem Onlinekurs Technische Mechanik 1 — TM1 (Technische Mechanik)

Lerne nun erfolgreich mit unserem Onlinekurs Werkstofftechnik 3 — WT3 (Werkstoffprüfung)

Perfekte Prüfungsvorbereitung für nur 14,90 EUR/Jahr pro Kurs

++ Günstiger geht’s nicht!! ++

Oder direkt Mitglied werden und Alle unsere Onlinekurse (inkl. Webinare + Unterlagen) sichern ab 7,40 EUR/Monat ++ Besser geht’s nicht!! ++